求解柔性作業車間調度問題的兩階段參數自適應蟻群算法

凌海峰 王西山

合肥工業大學過程優化與智能決策教育部重點實驗室，合肥，230009

0 引言

作業車間調度問題(job shop scheduling problem，JSSP)是一類受任務順序和配置要求約束的資源分配問題，屬于典型的NP－hard優化問題。而柔性作業車間調度(flexible job shop scheduling problem，FJSSP)則是JSSP問題的一個擴展，是指帶有機器柔性的作業車間調度問題，即每道工序有多個可供選擇的加工機器，更加符合實際生產情況，但也增加了問題求解的難度。

近年來，人們針對FJSSP問題的復雜性已經提出了許多有效的方法［1-3］。蟻群算法［4］作為一種新的群智能優化算法，采用正反饋機制且具有較強的通用性和魯棒性，已被成功地應用到作業車間調度問題中。但在實際應用中，蟻群算法存在易陷入局部最優和收斂速度慢等問題。針對此問題，王萬良等［5］提出了一種新的信息素更新策略，并用于求解FJSSP問題。Xing等［6］在采用蟻群算法求解FJSSP問題的過程中引入了知識模型，實驗得到的解的質量也優于目前的一些求解方法。Liouane等［7］將蟻群算法與禁忌搜索等局部搜索方法相結合，在求解FJSSP問題時能夠有效地避免算法陷入局部最優。研究發現，蟻群算法的性能對參數具有很強的依賴性［8-9］，而以上改進的蟻群算法在算法參數的設置上大都采用了經驗值，參數在算法的整個運行過程中處于不變的狀態，在一定程度上影響了蟻群算法的性能。

為了進一步提高蟻群算法在求解FJSSP問題時的性能，本文提出了一種新的兩階段參數自適應蟻群算法。在算法前期，采用細菌覓食趨化聚類技術判斷蟻群所處的狀態，進而動態地調整蟻群算法的參數，使算法快速收斂到全局最優解附近;在算法后期，利用混沌的隨機性和遍歷性特點來動態調整參數，有利于算法跳出局部最優。仿真實驗結果表明，該算法能夠有效地避免陷入局部最優，并在一定程度上提高了收斂速度。

1 問題的描述

1.1 FJSSP 問題描述

FJSSP問題描述如下:在m臺機器Mk(k=1，2，…，m)上加工 n 個工件 Jj(j=1，2，…，n)，每個工件包括 nj道工序，Oij(i=1，2，…，nj)表示工件Jj的第i個工序，并且每個工件的加工順序是預先確定的，每道工序都能夠在多臺機器上完成，不同機器加工同一道工序的時間往往不同并且是預先確定的，Tijk表示工序Oij在機器k上的加工時間。調度的目標是確定每道工序的加工機器、工序的開始加工時間和工序在每臺機器上的最佳加工順序，其目標函數為使所有工件在系統中的流通時間最短，具體可表示為:f=min(max(Cj))，j=1，2，…，n，其中Cj表示在某個調度中所有工件的總完工時間。此外，加工過程還需滿足以下約束條件:①每道工序在某一時刻只能在一臺機器上加工，且中途不能中斷;②同一工件的各道工序之間有先后約束，而不同工件的工序之間沒有這種約束;③在固定時刻每臺機器最多只能加工一道工序，且不同工件之間具有相同的優先級。

1.2 蟻群算法框架

蟻群算法是一種群智能隨機搜索算法，通過模擬大自然中螞蟻的覓食過程來實現問題的求解。真實的螞蟻在覓食過程中會在其經過的路徑上釋放信息素，且螞蟻傾向于向著信息素濃度高的方向移動。下面以旅行商問題為例描述蟻群算法的幾個主要步驟:①蟻群的初始化;②螞蟻按照狀態轉移概率選擇下一城市;③在蟻群完成一次搜索后，評價螞蟻個體，同時依據適應度函數值的大小更新各路徑上的信息素值;④判斷終止條件，如果滿足條件則結束，否則執行步驟②。

2 求解FJSSP問題的改進蟻群算法

2.1 初始解的產生

2.1.1 機器選擇

(1)建立矩陣M。將所有工件的工序Oij看作一個工件的工序Or(r=1，2，…，R，R表示所有工序的個數)。矩陣M中的元素Mrk=1/Trk，即矩陣M中的每個元素是由每道工序r在可選機器k上的加工時間的倒數構成的［10］。

(2)建立信息素初始化矩陣D。矩陣M經過歸一化處理后得到矩陣D，矩陣D表示工序在可選機器上的加工概率。則

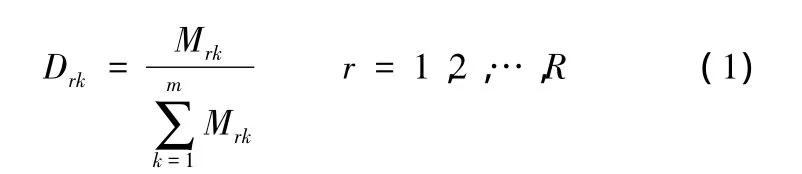
(3)依據矩陣D，應用輪盤賭方法為工序隨機選擇加工機器。

2.1.2工序排序

首先，將t時刻可在處于空閑狀態的機器k上加工的工序放入可選工序集合allow(k，t)中，然后利用啟發式信息根據下式計算t時刻可選工序集合中各道工序在機器k上的加工概率［10］(此概率也就是螞蟻的狀態轉移概率):

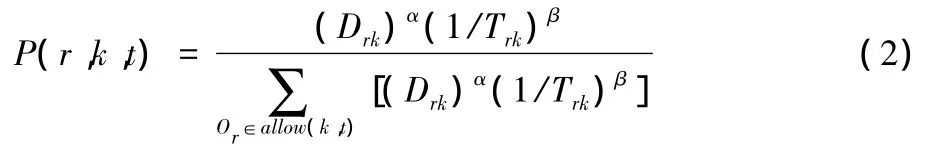
式中，α、β分別為表示信息素和可見度的重要程度參數。

然后，根據偽隨機比例規則對allow(k，t)中的工序進行排序，依據下式選擇下一工序Or:

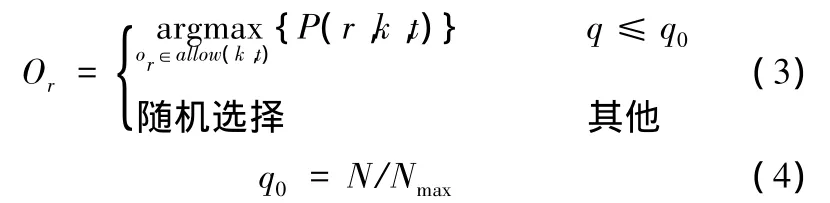
式中，N為本次迭代次數;Nmax為最大迭代次數;q為區間［0，1］上的服從均勻分布的隨機數，0≤q0≤1。

2.1.3總完工時間

目標函數總完工時間采用時間推進法的思想來計算［10］。 將初始化階段的仿真時鐘設為Stime=0，之后對比每臺機器上正在加工的工序到加工完成所需要的時間，選擇其中最小的一個t，并將仿真時鐘推進到Stime=t。循環以上操作，當所有的工序都完成加工時，Stime的值即為目標值總完工時間Cj。

2.2 基于細菌覓食趨化聚類的蟻群狀態判斷

研究人員在使用蟻群算法時發現，調整算法參數的時間往往多于算法設計和實施的時間，合適的參數設置對于算法的性能也有著至關重要的影響。同時，由于蟻群算法在問題的求解過程中蟻群會處于不同的搜索狀態，在不同的狀態下對參數的大小要求也不一樣［11-12］，對此，本文作出如下調整:在蟻群算法運行的前期，當所有螞蟻遍歷完全并找到各自的總完工時間時，使用趨化聚類算法對每只螞蟻找到的總完工時間進行聚類，并對蟻群的狀態作出判斷，然后基于蟻群狀態對參數進行動態調整。

2.2.1基于細菌覓食趨化的總完工時間聚類

細菌覓食算法是一種新的基于人類腸道大腸桿菌的覓食行為的全局隨機搜索算法，迭代過程主要包括趨化、復制和遷徙三種操作。文獻［13-14］將其應用到聚類問題中并獲得了不錯的結果。

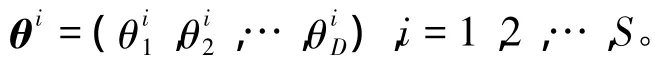
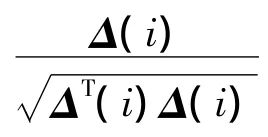
趨化操作結束后，所有的細菌將處于搜索空間中的特定位置，而細菌的最終位置將作為需要的聚類中心。因此，在螞蟻找到各自的總完工時間后，為了判斷蟻群所處狀態，本文對總完工時間進行趨化聚類，并記錄各類的規模以及最長、最短總完工時間所在類的規模。

2.2.2蟻群狀態判斷

在聚類規模已經統計好的基礎上，采用文獻［11］中的蟻群三種狀態規則來判斷蟻群所處狀態，從而為動態調整蟻群算法運行過程中的各個參數做好準備(表1)。其中，L表示最大規模的聚類大小，Mmid表示中間規模的聚類大小，S表示最小規模的聚類大小，W表示最長總完工時間所在的聚類規模，B表示最短總完工時間所在的聚類規模。

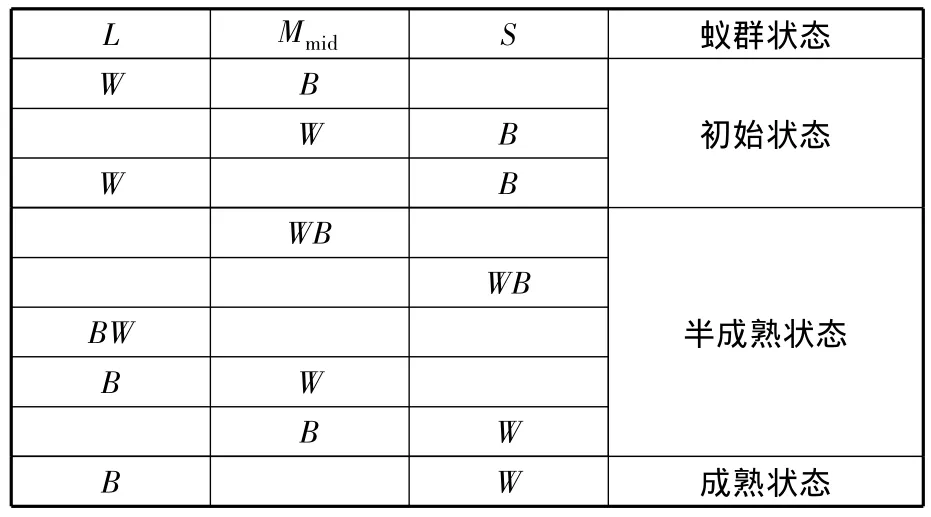
表1 蟻群三種狀態判斷規則表

為了更清晰地描述蟻群狀態，將表1概括如下:①當W ＞B時，即蟻群中大部分螞蟻還未找到最優總完工時間，說明蟻群正處于初始狀態;②當B=L且W=S時，即蟻群中大部分螞蟻已經找到了最優總完工時間，說明蟻群處于成熟狀態;③除上述兩種情況外，蟻群都處于半成熟狀態。

2.3 蟻群算法參數自適應調整

在蟻群狀態判斷完成之后，根據蟻群當前所處狀態來動態調整參數，但為了降低算法的復雜度，本文選擇當蟻群連續3次達到成熟狀態時，就跳出趨化聚類算法，即不再根據蟻群所處狀態對參數進行調整，此為算法運行的前期階段，這樣既能保證蟻群快速收斂到全局最優總完工時間附近，同時也節省了算法運行的時間成本;在此之后就是算法運行的后期階段，應用混沌理論來動態調整參數。

由于蟻群算法中有多個參數需要初始化，本文僅選取了對算法性能有關鍵性影響的3個參數(即信息素和可見度重要程度參數α、β以及信息素揮發系數ρ)來進行調整。

2.3.1基于蟻群狀態的參數調整

針對蟻群狀態的參數調整規則如下:①當蟻群處于初始狀態時，應該增加蟻群的搜索隨機性，即減小α、β、ρ的取值。②當蟻群處于半成熟狀態時，為了避免蟻群陷入局部最優，同時又要保證蟻群整體的收斂速度，應適當地減小α、β、ρ的取值。③當蟻群處于成熟狀態時，應該提高蟻群的收斂速度，即增大α、β、ρ的取值。

α、β、ρ的調整幅度及取值范圍如表2所示，其中Rrand為［0，1］區間內服從均勻分布的隨機數。為了使α、β、ρ能夠有更多、更精確的取值，本文采用隨機數的方式來控制各參數的調整幅度，仿真實驗結果也證明了這種方法的有效性。

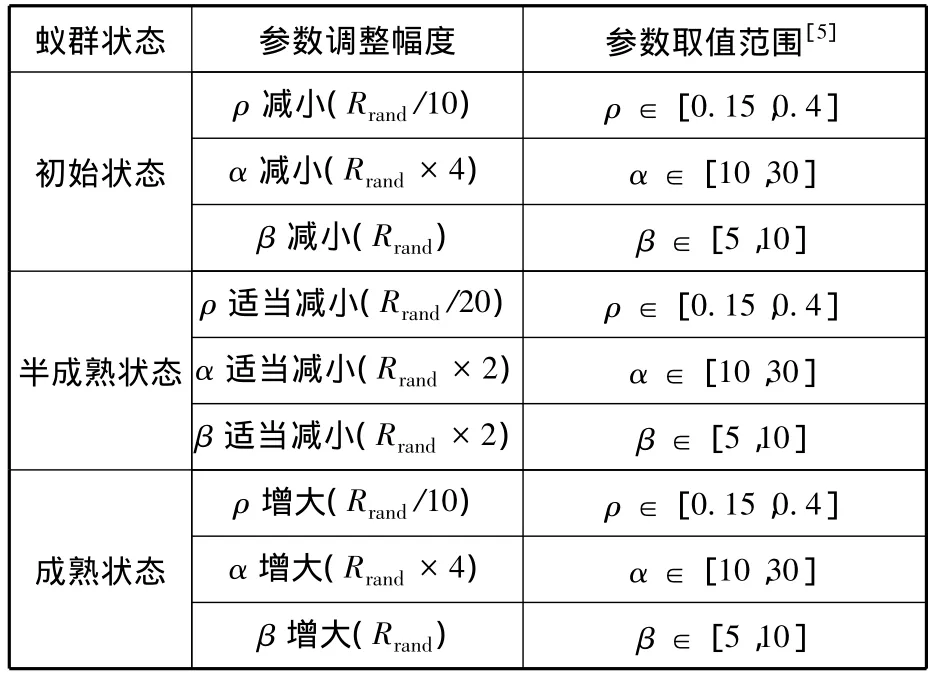
表2 蟻群狀態及參數調整

2.3.2基于混沌理論的參數調整

在最優總完工時間附近，為了避免蟻群算法陷入局部最優，同時能夠保持更好的隨機性來進行搜索，在α、β、ρ經過單位化處理后，采用經典的Logistic混沌映射來動態調整α、β、ρ。在混沌調整完成后再對各參數進行單位化處理后的恢復操作，以保證α、β、ρ取值的合理性。即

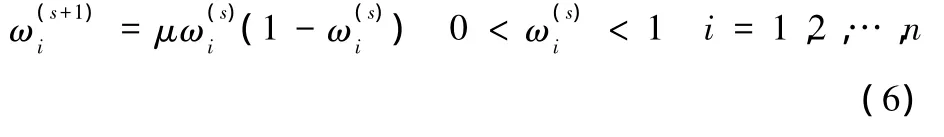
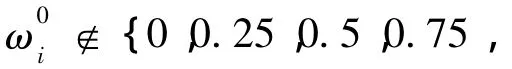
2.4 信息素更新規則

對搜索到最優總完工時間的螞蟻所走過的路徑上的信息素進行更新，其他路徑上的信息素只進行揮發。即

式中，ρ為信息素揮發系數;Mmakespan為到目前為止找到的全局最優總加工時間。

對更新后的矩陣M進行歸一化處理后得到新的信息素矩陣D，此時信息素的更新就已經完成了，接下來判斷算法是否滿足終止條件，如果滿足，則結束;否則繼續下一次的迭代。

2.5 算法實現步驟

應用改進的蟻群算法求解FJSSP問題的具體實現步驟如下:

(1)初始化參數α、β、ρ，并初始化信息素矩陣D，在開始工序節點上放置Mg只人工螞蟻。

(2)依據信息素矩陣，應用輪盤賭方法對機器進行選擇。

(3)初始化所有螞蟻的可允許工序集合allow(m，t)，并把所有工件的第一道工序放入allow(m，t)中，開始螞蟻的遍歷過程。

(4)計算出所有螞蟻的狀態轉移概率，并根據偽隨機比例規則選擇目標工序Or。

(5)如果螞蟻遍歷了所有工序，即allow(m，t)中不存在未加工的工序，則轉至步驟(6);否則執行步驟(4)。

(6)當所有螞蟻都遍歷完成后，記錄每只螞蟻搜索到的總完工時間Cj。

(7)N←N+1。

(8)檢查本次迭代之前的三代蟻群狀態，若前三代均為成熟狀態，則對α、β、ρ進行單位化處理后根據式(6)進行調整，調整完成后再對它們進行單位化后的恢復操作，并將此代蟻群狀態置為成熟狀態;否則用趨化聚類算法對總完工時間進行聚類，判斷蟻群當前所處狀態，并根據表2對α、β、ρ進行調整。

(9)根據式(7)和式(8)對信息素進行更新。

(10)如果N≤Nmax，則轉至步驟(2)繼續迭代;否則終止算法并輸出結果。

改進算法的流程圖如圖1所示。

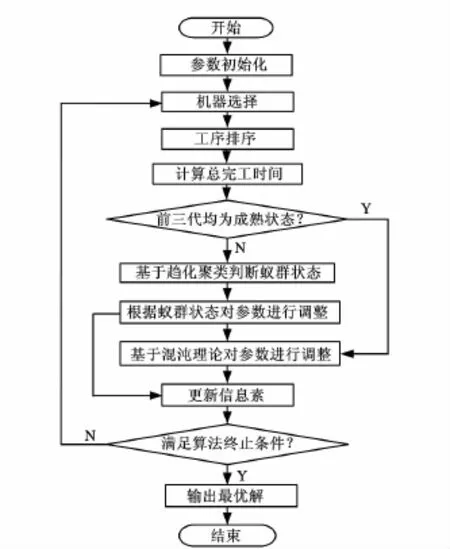
圖1 改進算法的流程圖

3 仿真實驗

3.1 聚類準確性比較實驗

本文的參數調整建立在聚類的基礎之上，因此，聚類結果的準確性直接關系到參數的調整，進而影響整個算法的求解性能。為了驗證基于趨化操作的聚類算法的準確性，本文采用文獻［14］中的正確率定義方法，并用UCI數據集中的Iris數據和Wine數據進行了測試實驗。即

式中，C為聚類正確率;Cd為被分配到正確聚類簇中的數據個數;Ct為總數據個數。

趨化聚類算法運行10次后所得到的聚類正確率的平均值和文獻［14］中各算法的聚類比較結果如表3所示。

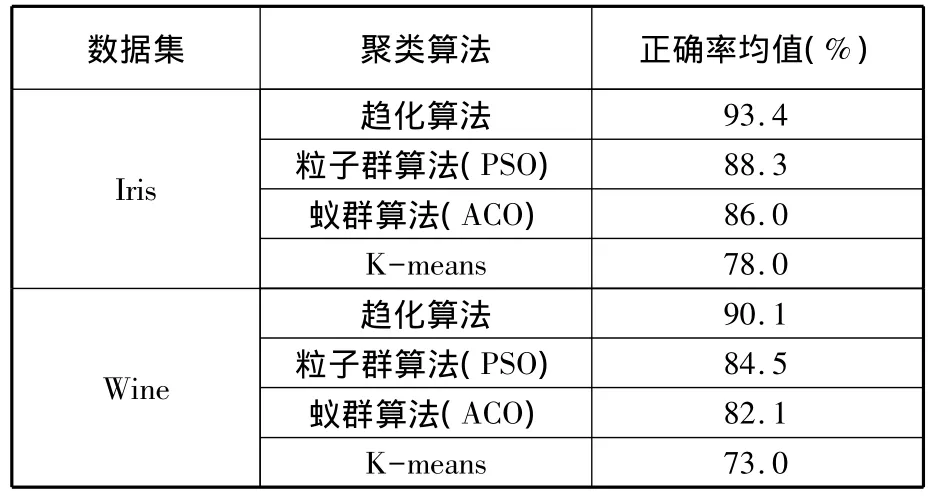
表3 測試數據結果比較

3.2 FJSSP 仿真實驗

為了驗證本文改進算法的有效性，采用文獻［10］中的柔性作業車間調度數據進行實驗仿真，該加工系統有4臺機器，要加工5個工件，每個工件有3至5道工序，如表4所示。如工序O11表示第一個工件的第一道工序，可由機器3用48min完成，或者由機器4用40min完成。同時根據文獻［5］中所確定的蟻群算法主要參數的最優取值范圍來確定參數的初始值和取值范圍，即Mg=40，Nmax=300，α ∈［10，30］，β ∈［5，10］，ρ∈［0.15，0.4］。

表4 工件的工序及加工機器和加工時間

本文改進算法BFAC與文獻［10］中的蟻群算法各自運行30次后的實驗結果如表5所示。

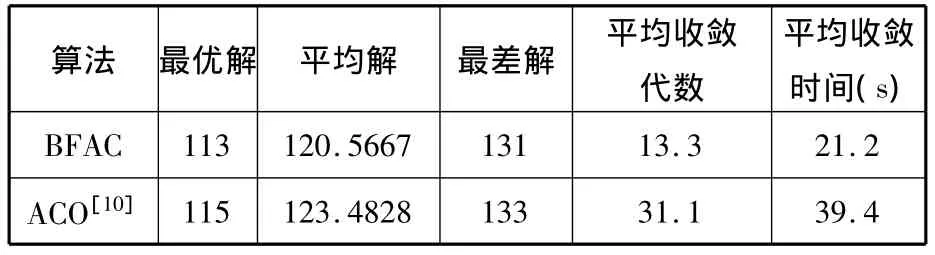
表5 實驗對比結果

從表5可以看出，本文改進算法能夠有效地避免陷入局部最優，找到更好的全局最優解，且改進后的算法較改進前有更好的穩定性。同時，本文改進算法能夠在13代左右就收斂到全局最優解，且改進算法的平均收斂時間也有所縮短，在一定程度上提高了算法的收斂速度。歷代最優解收斂曲線如圖2所示。

為了進一步驗證本文改進算法的有效性，分別與文獻［5］、［15-18］中的算法結果進行了比較，最優解為算法運行30次后的最優結果，如表6所示。

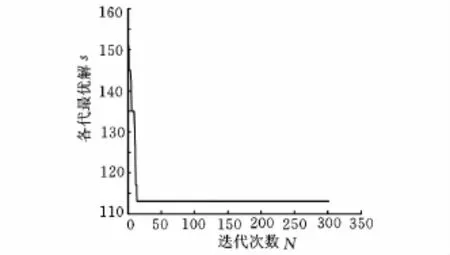
圖2 歷代最優解收斂曲線

從表6可以看出，本文改進算法在與文獻中的算法進行比較時，能夠找到更好的全局最優解。其中在6臺機器4個工件的問題求解中，文獻［5］中的算法在30代左右收斂到了最優解，而本文改進的算法平均在5代以內就能夠收斂到最優解且30次運行均找到了最優解17。此外，本文改進的算法求得的解的平均值基本上要小于文獻中的平均值。以上仿真結果都證明了本文算法的有效性。

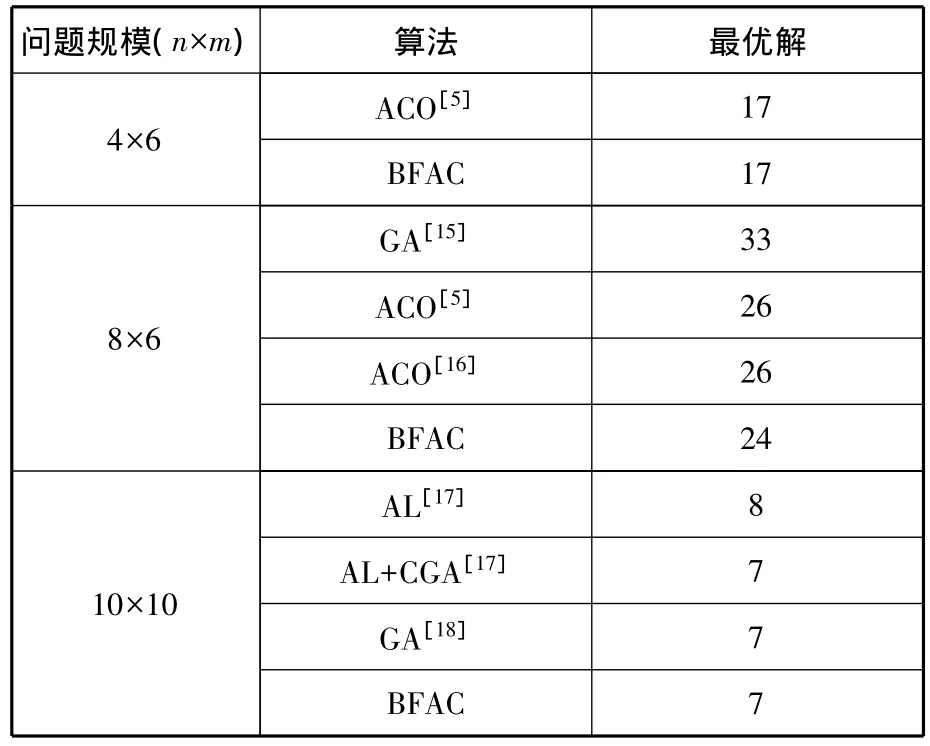
表6 改進算法與文獻中算法的比較結果

4 結語

本文在蟻群算法求解FJSSP問題的模型基礎上，提出了基于聚類和混沌相結合的自適應參數調整方法。從仿真實驗結果可以看出，新算法在保證一定收斂速度的基礎上能夠有效地避免陷入局部最優解，表現出了良好的全局搜索能力和魯棒性，能夠有效地解決FJSSP問題。今后將進行更廣泛的測試并對該方法作適當的改進。此外，將這種新的參數調整策略應用到其他群智能優化算法也是一個值得研究的方向。

［1］宋莉波，徐學軍，孫延明，等.一種求解柔性工作車間調度問題的混合遺傳算法［J］.管理科學學報，2010，13(11):49-54.Song Libo，Xu Xuejun，Sun Yanming，et al.A Hybrid Genetic Algorithm for Flexible Job Shop Scheduling Problem［J］.Journal of Management Sciences in China，2010，13(11):49-54.

［2］陳勇，阮幸聰，魯建廈，等.基于元胞機和改進 GA的大型零件柔性作業車間調度算法［J］.中國機械工程，2012，23(2):177-184.Chen Yong，Ruan Xingcong，Lu Jiansha，et al.Flexible Job Shop Scheduling Algorithm of Large Parts Based on Cellular Automata and Improved GA［J］.China Mechanical Engineering，2012，23(2):177-184.

［3］賈兆紅，陳華平，孫耀暉.混合粒子群算法在柔性工作車間調度中的應用［J］.系統仿真學報，2007，19(20):4743-4747.Jia Zhaohong，Chen Huaping，Sun Yaohui.Hybrid Particle Swarm Optimization for Flexible Job Shop Scheduling［J］.Journal of System Simulation，2007，19(20):4743-4747.

［4］Dorigo M，Maniezzo V，Colorni A.Ant System:Optimization by a Colony of Cooperating Agents［J］.IEEE Transaction on System，Man and Cybernetics，1996，26(1):29-41.

［5］王萬良，趙澄，熊婧，等.基于改進蟻群算法的柔性作業車間調度問題的求解方法［J］.系統仿真學報，2008，20(16):4326-4329.Wang Wanliang，Zhao Cheng，Xiong Jing，et al.Method to Resolve Flexible Job Shop Scheduling Problem Based on Improved Ant Colony Algorithm［J］.Journal of System Simulation，2008，20(16):4326-4329.

［6］Xing L N，Chen Y W，Wang P，et al.A Knowledgebased Ant Colony Optimization for Flexible Job Shop Scheduling Problems［J］.Applied Soft Computing，2010，10(3):888-896.

［7］Liouane N，Saad I，Hammadi S，et al.Ant Systems ＆Local Search Optimization for Flexible Job Shop Scheduling Production［J］.International Journal of Computers，Communications ＆ Control，2007，2(2):174-184.

［8］Dorigo M，Birattari M，Stutzle T.Ant Colony Optimization［J］.IEEE Computational Intelligence Magazine，2006，1(4):28-39.

［9］Favaretto D，Moretti E，Pellegrini P.On the Explorative Behavior of Max－Min Ant System［C］//Engineering Stochastic Local Search Algorithms.Designing，Implementing and Analyzing Effective Heuristics.SLS 2009，LectureNotesin ComputerScience.Heidelberg:Springer，2009:115-119.

［10］魯麗君，何向軍.改進蟻群算法在柔性作業車間調度中的應用研究［D］.北京:首都經濟貿易大學，2012.

［11］焦淑娟，張軍.蟻群算法中基于PAM聚類算法的參數調整［D］.廣州:中山大學，2008.

［12］Gong Y，Xu R，Zhang J，et al.A Clustering－based A-daptive Parameter Control Method for Continuous Ant Colony Optimization［C］//Proc.of the Systems，Man and Cybernetics.San Antonio，2009:1827-1832.

［13］Wan M，Li L，Xiao J，et al.Data Clustering Using Bacterial Foraging Optimization［J］.Journal of Intelligent Information Systems，2012，38(2):321-341.

［14］凌海峰，王浩.細菌覓食算法與K－means結合的Web用戶會話聚類［J］.計算機工程與應用，2012，48(36):121-124.Ling Haifeng，Wang Hao.Integration of Bacterial Foraging with K－means for Web User Session Clustering［J］.Computer Engineering and Applications，2012，48(36):121-124.

［15］余琦瑋，趙亮，潘雙夏.基于遺傳算法的柔性作業車間調度優化［J］.組合機床與自動化加工技術，2004，46(4):32-34.Yu Qiwei，Zhao Liang，Pan Shuangxia.A Scheduling Optimization of Flexible Job Shop Using Genetic Algorithm［J］.Modular Machine Tool＆ Automatic Manufacturing Technique，2004，46(4):32-34.

［16］亓凌，楊建棟，李保，等.基于自適應蟻群算法的柔性作業車間調度問題［J］.機電工程，2010，27(2):46-49.Qi Ling，Yang Jiandong，Li Bao，et al.Flexible Job Shop Scheduling Problem Based on Adaptive Ant Colony Algorithm［J］.Journal of Mechanica ＆ Electrical Engineering，2010，27(2):46-49.

［17］Kacem I，Hammadi S，Borne P.Approach by Localization and Multiobjective Evolutionary Optimization for Flexible Job－shop Scheduling Problems［J］.IEEE Transactions on Systems，Man and Cybernetics，2002，32(1):1-13.

［18］張國輝，高亮，李培根，等.改進遺傳算法求解柔性作業車間調度問題［J］.機械工程學報，2009，45(7):145-151.Zhang Guohui，Gao Liang，Li Peigen，et al.Improved Genetic Algorithm for the Flexible Job Shop Scheduling Problem［J］.Journal of Mechanical Engineering，2009，45(7):145-151.