基于方位特征集的兩轉動(0T－2R)并聯機構的型綜合及其應用

鄧嘉鳴 尹洪波 沈惠平 李 菊 楊廷力

常州大學，常州，213016

0 引言

目前，國內外對并聯機構進行型綜合的理論與方法主要有三種，即基于位移子群的方法、基于螺旋理論的方法及基于方位特征(position and orientation characteristics，POC)集的方法，且人們已運用上述三種方法綜合出了較多并聯機構新機型。應用基于位移子群的方法，文獻［1-4］先后研究了三自由移動并聯機構、三自由度球面并聯機構以及非對稱的2T1R和1T2R三自由度并聯機構的型綜合;李秦川等［5］綜合出4種三移動并聯機構。應用基于螺旋理論的方法，Kong等［6］、Fang等［7］分別對球面并聯機構、4～5個自由度過約束并聯機構進行了型綜合;黃真及其團隊對3～5個自由度對稱并聯機構進行了綜合，并得到了30多種可實現連續運動的對稱五自由度并聯機構［8-9］。應用基于方位特征的方法，楊廷力及其團隊對并聯機構的拓撲結構設計進行了系統研究，沈惠平等［10-11］分別對三平移與六自由度并聯機構進行了型綜合，分別得到26種與10種機型;羅玉峰等［12-13］分別對兩平移兩轉動與三平移一轉動并聯機構進行了型綜合，分別得到27種與43種機型;文獻［14］綜合出了43種三自由度并聯機構、31種四自由度并聯機構、22種五自由度并聯機構，以及8種六自由度并聯機構。

兩轉動并聯機構具有結構簡單、實用性強的特點，主要應用于機器人關節、衛星天線的方位跟蹤系統、攝像機定位系統以及醫療器械等方面，因而具有重要的實用價值，但目前對兩自由度并聯機構的型綜合研究較少。高峰等［15］利用GF集理論進行型綜合，列出了以符號組合形式表示的26種兩支路結構的機型，給出了4種機構的簡圖;曾達幸等［16］根據運動綜合法思想，提出了一種轉動解耦并聯機構的機型綜合方法，并綜合出多種兩自由度轉動解耦并聯機構;東昕［17］基于現有的三種兩自由度球面并聯機構(Omni－WristⅢ機構、球面5R 機構、3－RSR＆1－SS機構)，提出了兩種新型的球面并聯機構，并從中優選出一種能滿足噴泉運動要求的構型。

本文應用基于POC集的機構型綜合方法，對兩轉動(0T－2R)輸出并聯機構進行了拓撲結構綜合，得到了14種機型，其中，6種機型為本方法綜合得到，然后按它們的結構特性進行了初步分類，并將優選的一種兩轉動并聯機構用于太陽能二軸跟蹤機構的研制。

1 兩轉動并聯機構的型綜合及其結構分析

基于POC集的并聯機構型綜合理論與方法詳見文獻［14］，這里只給出主要步驟。

1.1 確定期望得到的機構的POC集Mpa

Mpa的表達式如下:

其中，t0表示不存在有限移動，r2表示存在兩個有限轉動。

1.2 支路結構的綜合

(1)支路的POC集。并聯機構的POC方程:

式中，Mbj為當其他支路不在時，第j條SOC支路末端構件的POC集。

并聯機構的POC集是各支路POC集的交集，于是，支路的POC集可取為

(2)支路的結構類型。滿足上述POC集的簡單支路(SOC)與復合支路(HSOC)的結構類型如表1所示。

1.3 支路組合方案

利用表1中的SOC支路和HSOC支路，可綜合出表2所示的組合方案。

現以表2中C3支路的組合方案為例，綜合1個兩轉動(0T－2R)并聯機構。C3支路的組合方案為

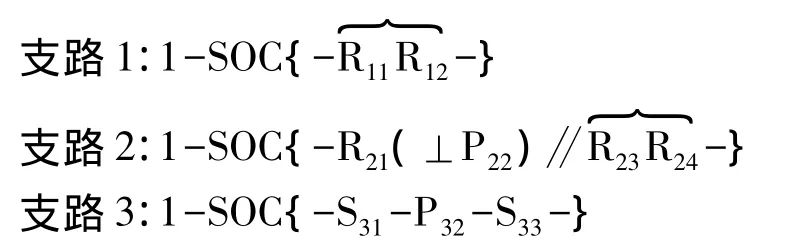
1.4 確定支路在兩平臺裝配的幾何條件

(1)確定支路末端構件的POC集。

支路1:

表1 SOC與HSOC的結構類型

表2 并聯機構的支路組合方案

(續表2)

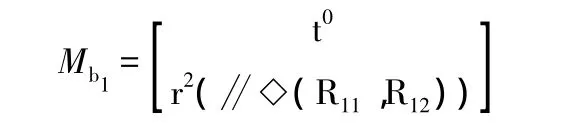
其中◇(R11，R12)表示由 R11、R12構成的平面，下同。

支路2:

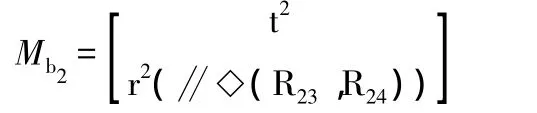
支路3:

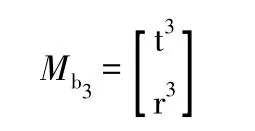
(2)建立并聯機構POC方程:

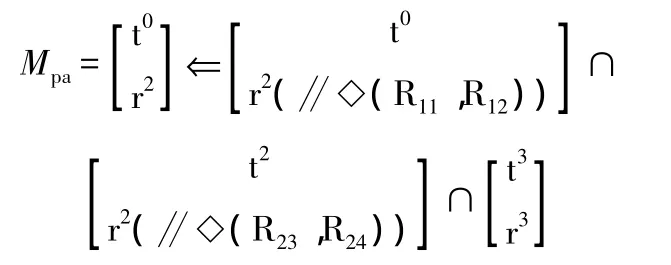
(3)確定支路在兩平臺裝配的幾何條件。為實現動平臺的兩維轉動，應使兩支路POC的交集保留兩個獨立轉動元素，即裝配的幾何條件為:R11與R12正交，R11∥R23∥R21且R12與R24的軸線重合。

(4)畫出機構簡圖。根據各支路拓撲結構特征以及支路在兩平臺裝配的幾何條件，畫出機構簡圖，如圖1所示。

1.5 檢驗機構自由度

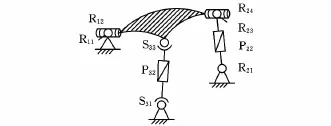
圖11 -SOC{-}⊕1-SOC{-R(⊥P)∥-}⊕1-SOC{-S-P-S-}

(1)確定第一個獨立回路的獨立位移方程數ξL1。第一、二條支路組成的第一個獨立回路的ξL1為

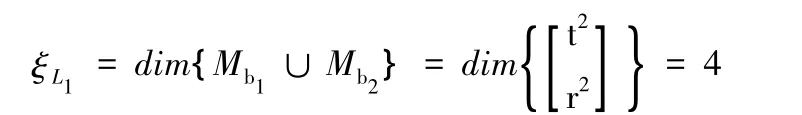
式中，dim{}為求維數的函數。

第一條、第二條支路組成的子并聯機構的自由度為

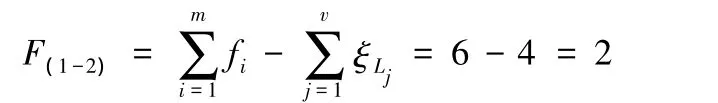
(2)第一條、第二條支路組成的子并聯機構動平臺的POC集為

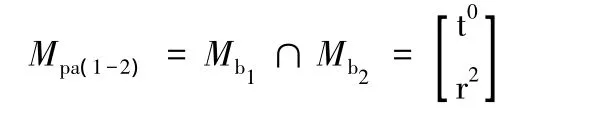
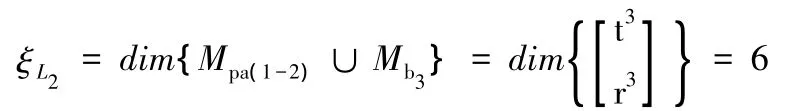
(4)確定并聯機構自由度:

1.6 判斷機構消極運動副

由消極運動副的判斷準則［14］，判斷R24副是否為消極運動副。

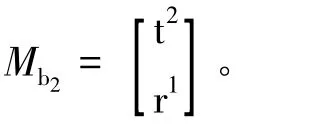
(2)確定新機構的自由度。首先確定由第一條、第二條支路組成的第一個獨立回路的獨立位移方程數ξL1:

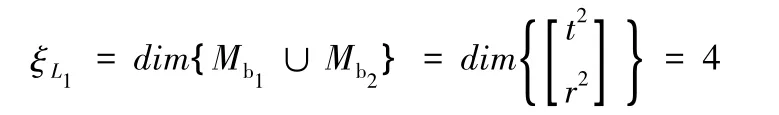
第一條、第二條支路組成的子并聯機構的自由度為

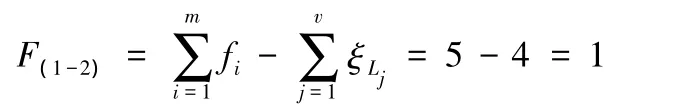
第一條、第二條支路組成的子并聯機構動平臺的POC集為

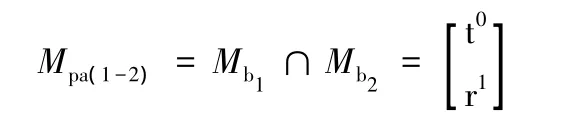
然后再確定第二個獨立回路的獨立位移方程數ξL1:

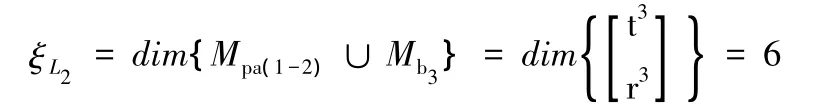
最后可得到并聯機構的自由度:

(3)判斷消極運動副。由于新機構的自由度為1，而原機構的自由度為2，則被剛化的運動副不是消極運動副。

1.7 選取機構的驅動副

基于驅動副判定準則［14］，判定圖1中機構的P22與P32副可否同時為驅動副。

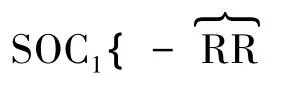
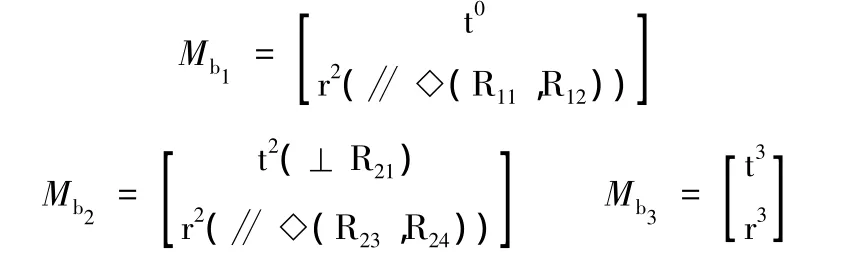
第二支路的自由度為3，可在Mb2中任選3個為獨立元素，則另外一個為非獨立元素;第三支路的自由度為5，可在Mb3中任選5個為獨立元素，則另外一個為非獨立元素。

(2)確定新機構的自由度。

首先確定的第一條、第二條支路組成的第一個獨立回路的獨立位移方程數ξL1。

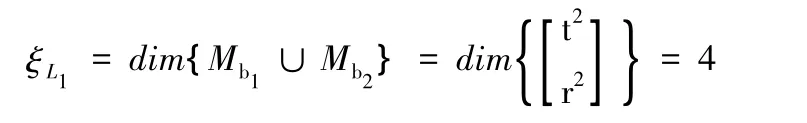
其中，Mb2取兩個有限移動和一個有限轉動為獨立元素。

第一條、第二條支路組成的子并聯機構的自由度為

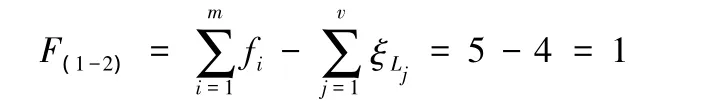
第一條、第二條支路組成的子并聯機構動平臺的POC集為

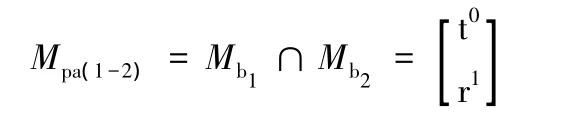
然后，確定第二個獨立回路的獨立位移方程數ξL2:

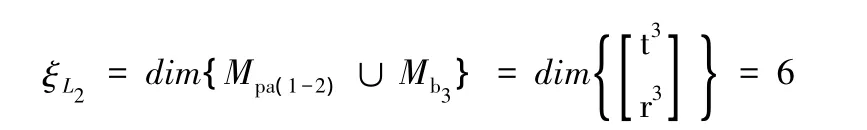
其中，在Mb3中取t3為獨立元素。

最后確定并聯機構的自由度:

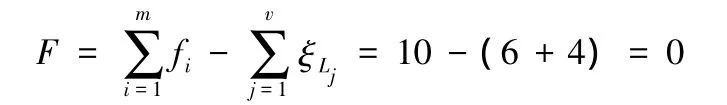
(3)判定P22與P32副可否同時為驅動副。

由于新機構的自由度0，按照驅動副判定準則，圖1所示的機構同一平臺上的P22與P32副可同時為驅動副。

1.8 確定并聯機構的拓撲結構

(1)支路拓撲結構。

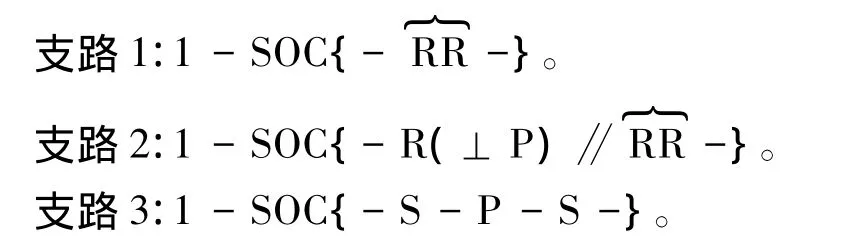
(2)兩平臺的拓撲結構。

動平臺上:R11與R12正交，R11∥R23且R12與R24的軸線重合。

靜平臺上:R11∥R21。

1.9 并聯機構拓撲結構的特性分析

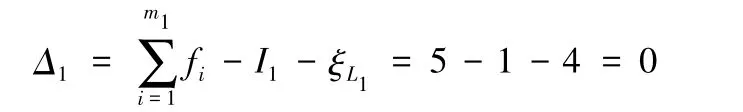
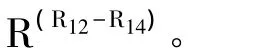
取第二個單開鏈為SOC{－R(R12－R14)－S31－P32－S33－}。需計入繞R12與R24公共軸線的轉動 R(R12－R14)，其約束度 Δ2為

由BKC的判定方法可知，該機構包含兩個BKC，其耦合度為

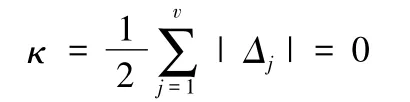
(2)自由度類型。基于自由度類型判定準則，該機構具有部分自由度。

(3)運動輸入－輸出解耦性。基于拓撲結構的解耦原理，已知該機構具有部分自由度，因此具有運動輸入－輸出解耦性。

2 拓撲結構類型的分類

按照上述綜合方法，選取表2中其他組合方案，已綜合出了14種機型，如表3所示。進一步，按支路類型、是否含有復雜支路、是否具有解耦性、運動學與動力學復雜性，以及轉動輸出類型，對表3中的機構進行分類，以供設計人員參考與選用。

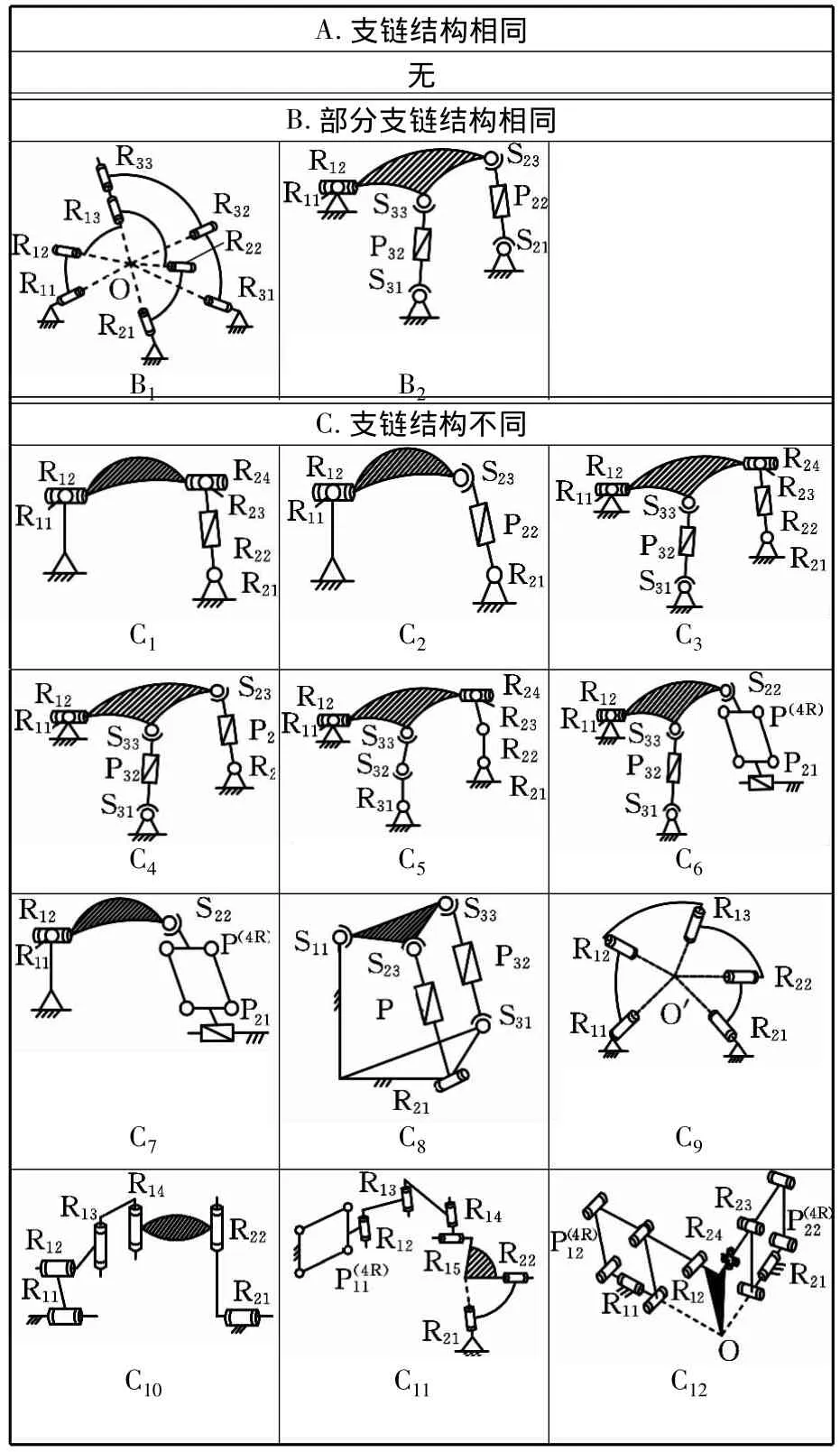
表3 兩轉動(0T－2R)并聯機構拓撲結構

(1)是否含有相同支路的并聯機構:①無所有支路相同的并聯機構;②兩條支路相同的并聯機構，如表3中B1、B2所示機構;③支鏈結構不同的并聯機構。如表3中C1～C12所示的機構。

(2)含有復雜支路的并聯機構:表3中C6、C11、C12所示的機構。

(3)具有運動解耦性的機構:表3中B2、C1～C8、C10～C12所示的機構。

(4)基于耦合度的運動(動力)學復雜性。已計算所綜合出的14種并聯機構耦合度值均為0，因此，可直接得到其運動學、動力學解析式，其分析過程較為簡單。

(5)轉動輸出類型。根據文獻［18-20］，兩轉動輸出機構分為純球面轉動、非球面轉動兩種情況，因此，表3中，作純球面轉動的有 B1、C9，其他均為非球面轉動，這有利于不同類型應用場合時選用。

3 優選機型的設計與應用

已綜合出的 14 種機型(表 3)中，B1、B2、C1、C2、C9、C10、C11、C12已有相應文獻報道，而 C3，C4，…，C8這6種機型為作者按照上述理論方法新綜合得到，這些新機型為二自由度的轉動關節、衛星天線的方位跟蹤系統、攝像機定位系統等提供了侯選設計方案。筆者已將C3機型用于太陽能二軸跟蹤機構，其機構設計如圖2所示，并已對該機構進行了運動學性能分析，包括機構工作空間、機構誤差分析，并運用遺傳算法對機構的結構參數進行了優化計算，其工作空間如圖3所示，其樣機研制在進行中。

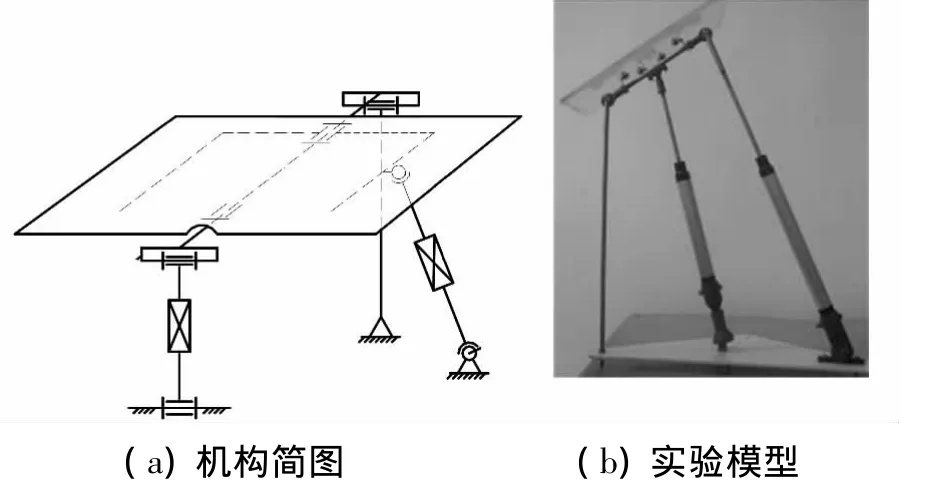
圖2 二自由度太陽能跟蹤機構

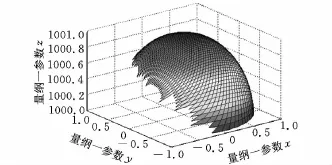
圖3 二軸跟蹤機構的工作空間

5 結論

(1)根據基于方位特征集的拓撲結構設計理論，對兩轉動(0T－2R)并聯機構進行了型綜合，得到了14種機型，其中8種機型已有文獻報道，而6種機型為筆者按照上述理論方法綜合得到，這些機型為二自由度的轉動關節、衛星天線的方位跟蹤系統、攝像機定位系統的實用與設計等提供了優選設計方案。

(2)該方法運算規則少、數學方法簡單，幾何與物理意義明確，適用于所有無過約束和一般過約束機構。

［1］Hervé J M，Sparacino F.Structural Synthesis of Parallel Robots Generating Spatial Translation［C］//5th IEEE International Conference on Advanced Robotics.Pisa，Italy，1991:808-813.

［2］Karouia M，Hervé J M.A Family of Novel Orientational 3－DOF Parallel Robots.Robotics Manufacturing Systems［C］//14th CISM－IFToMM Symposium.Udine，Italy，2002:359-368.

［3］Karouia M，Hervé J M.Asymmetrical 3－dof Spherical Parallel Mechanisms［J］.European Journal of Mechanics A/Solids，2005，24:47-57

［4］Lee C C，Herve J M.Translational Parallel Manipulators with Doubly Planar Limbs［J］.Mechanism and Machine Theory，2006，41(4):433-455.

［5］李秦川，黃真.基于位移子群分析的3自由度移動并聯機構型綜合［J］.機械工程學報，39(6):18-21.Li Qinchuan，Huang Zhen.Type Synthesis for 3－DOF Translation Parallel Mechanisms Based on Displacement Subgroup［J］.Chinese Journal Mechanical Engineering，39(6):18-21.

［6］Kong X W，Gosselin C M.Type Synthesis of 3－DOF Spherical Parallel Manipulators Based on Screw Theory［C］//Proceedings of ASME Design Engineering Technical Conferences.Montreal，2002:MECH-34259.

［7］Fang Y F，Tsai L W.Structure Synthesis of a Class of 4－DOF and 5－DOF Parallel Manipulators with Identical Limb Structures［J］.Int.J.Rob.Res.，2002，21:799-810.

［8］Huang Z，Li Q C.Type Synthesis of Symmetrical Lower－mobility Parallel Mechanisms Using Constraint－synthesis Method［J］.Int.J.Rob.Res.，2003，22:59-79.

［9］Li Q C，Huang Z.A Family of Symmetrical Lower－mobility Parallel Mechanism with Spherical and Parallel Subchains［J］.J.Rob.Syst.，2003，20(6):297-305.

［10］余同柱，沈惠平，鄧嘉鳴，等.方位特征集法在三平移并聯機構型綜合中的應用［J］.機械設計，2012，29(8):48-54.Yu Tongzhu，Shen Huiping，Deng Jiaming，et al.Application of POC Set Method in Structure Synthesis of 3－translation Parallel Manipulator［J］.Journal of Machine Design，2012，29(8):48-54.

［11］鄧嘉鳴，余同柱，沈惠平，等.基于方位特征的六自由度并聯機構型綜合［J］.中國機械工程，2012，23(21):2525-2640.Deng Jiaming，Yu Tongzhu，Shen Huiping，et al.Type Synthesis for 6－DOF Novel Parallel Mechanisms Based on POC Set Method［J］.China Mechanical Engineering，2012，23(21):2525-2640.

［12］羅玉峰，姚偉科，石志新，等.基于方位特征集的兩平移兩轉動并聯機構拓撲結構綜合與分類［J］.機床與液壓，2011，39(3):22-25.Luo Yufeng，Yao Weike，Shi Zhixin，et al.Structure Synthesis and Classification of 2－Translation and 2－Rotation Parallel Manipulator Based on POC Approach［J］.Machine Tool ＆ Hydraulics，2011，39(3):22-25.

［13］羅玉峰，劉卓，石志新，等.三平移－轉動并聯機構型綜合及分類［J］.機械設計與研究，2010，26(5):40-43.Luo Yufeng，Liu Zhuo，Shi Zhixin，et al.Structural Synthesis and Classification of 3－Translation and 1－ratation Parallel Manipulator［J］.Machine Design and Research，2010，26(5):40-43.

［14］楊廷力，劉安心，羅玉峰，等.機器人機構拓撲結構設計［M］.北京:科學出版社，2012.

［15］高峰，楊加倫，葛巧德.并聯機器人型綜合的GF集理論［M］.北京:科學出版社，2011.

［16］曾達幸，黃真.基于螺旋理論的轉動解耦并聯機構型綜合［J］.中國科學:技術科學，2011，41(5):585-591.Zeng Daxing，Huang Zhen.Type Synthesis of the Rotational Decoupled Parallel Mechanism Based on Screw Theory［J］.Sci.China Tec.Sci.，2011，41(5):585-591.

［17］東昕.2－DOF類球面并聯轉臺的設計及應用研究［D］.北京:北京航空航天大學，2011.

［18］Gogu G.Structural Synthesis of Parallel Robots，Part 4:Other Topologies with Two and Three Degrees of Freedom［M］.Berlin:Springer－Verlag，2012.

［19］Wu K，Yu J J，Zong G H，et al.Type Synthesis of 2－dof Rotational Parallel Manipulators with an Equal－diameter Spherical Pure Rolling Motion［C］//The 2013 ASME International Design Engineering Technical Conferences.Oregon，Portland，2013:DETC2013-12305.

［20］Wu K，Yu J J，Li S Z，et al.Type Synthesis of Two Degrees－of－Freedom Rotational Parallel Mechanisms with a Fixed Center－of－Rotation Based on a Graphic Approach［C］//The 2012 ASME International Design Engineering Technical Conferences.Chicago，USA，2012:ASME DETC2012-71028.