基于道路勢場的車道偏離自動校正自適應控制

汪明磊 陳無畏 王家恩

合肥工業大學，合肥，230009

0 引言

車道偏離自動校正系統的作用是當駕駛員疲勞或其功能喪失時自動控制車輛沿車道中心線行駛，即控制車輛跟蹤目標路徑。該系統可根據車輛當前的行駛狀態和它與道路之間的相對運動關系，按照一定的控制策略綜合控制車輛，使它的行駛軌跡與目標路徑間的偏差能夠滿足目標函數的指標要求，同時保證車輛的行駛安全性和乘坐舒適性［1-2］。跟蹤控制系統的控制方法主要包含以下兩類［3］:①基于車輛當前位置與期望路徑之間橫向距離偏差與方位偏差的位置偏差反饋控制系統［4-5］。陳無畏等［4］以當前路徑信息作為反饋，以未來路徑信息作為預瞄，設計了預瞄加反饋的控制器，預瞄距離和智能車速度根據預瞄路徑的彎曲程度自動調整。游峰等［5］提出了一種基于車輛位置誤差模型的積分誤差Back-stepping控制方法。這些都是以車輛前方或當前位置的車-路相對位置偏差作為輸入，使用各種反饋控制方法，基于車輛運動學模型設計反饋控制系統。由于沒有考慮車輛的動力學特性，無法滿足實際要求。同時由于車輛系統的時間滯后性，控制過程中會存在大的延遲環節，因此存在控制精度不高、實時性差的缺點。②通過期望路徑產生描述車輛運動的期望動力學物理量，然后通過車輛狀態反饋進行跟蹤控制［6-8］。這類控制方法主要是根據期望路徑計算出描述車輛跟蹤目標路徑的車輛自身物理量，如車輛橫擺角速度、側向加速度等，然后設計反饋控制系統來跟蹤這些物理量。王家恩等［7］基于車輛期望橫擺角速度進行了路徑跟蹤橫向控制。高振海［8］則根據“最優曲率模型”，提出了基于側向加速度的方法。但是他們都只設計了單一的期望物理量，而且在設計期望物理量時又只考慮了車輛與期望路徑之間橫向距離偏差。由于車輛在行駛過程中側向加速度與橫擺角速度共同影響著車輛的橫向運動狀態，因此隨著縱向車速的變化，該類方法會出現較大的跟蹤誤差和跟蹤穩定性問題。

對于車道偏離自動校正系統的實時控制，可通過構筑包含道路環境信息的人工勢場［9-10］，快速計算勢場力，實現在線控制車輛行駛軌跡。Rossetter等［9］闡述了一種由基于危險度的道路勢場產生控制力的車道保持系統。Brandt等［10］利用道路勢場的概念，通過給道路邊緣及障礙物設定危險度，規劃出一條無障礙路徑。本文在建立道路勢場的基礎上，由勢場力推算車輛期望側向加速度和期望橫擺角加速度，進而控制車輛跟蹤目標路徑。道路勢場函數值能夠直觀地表現車輛所處的環境危險水平，即勢場函數最小值位于道路中心線，隨著車輛與道路中心線橫向距離的增大，勢場函數值逐漸增大。勢場函數值由車輛在勢場中所處的位置決定，它包含了車輛與道路中心線之間的橫向距離偏差及方位偏差信息。道路環境信息及車輛在勢場中所處的位置可通過車載傳感器實時探測。

1 車輛模型及道路勢場的構建

1.1 車輛運動學模型

本文所研究的路徑跟蹤控制方法是以虛擬人工勢場為基礎的，首先需要建立基于位置的道路人工勢場。該勢場對處于其中的車輛具有力的作用，而勢場力的大小又與車輛在勢場中的位置(即車輛與道路的相對位置)密切相關。

在某一時刻，車輛質心在大地坐標系XOY中(圖1)的位置Oc坐標為(Xc，Yc)，車輛縱軸線與橫坐標的夾角為φc。假設車輛質心處速度為vc，質心側偏角為β，車輛當前橫擺角速度為ωr，則上述參數的關系為

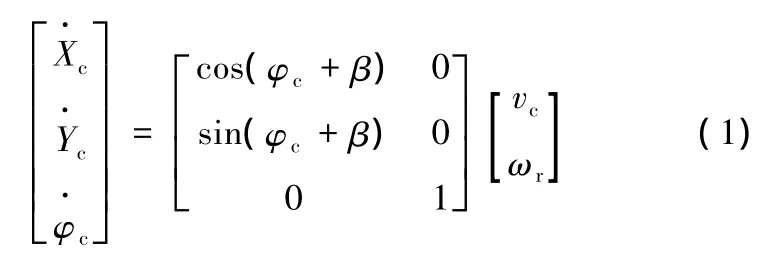
這里規定質心側偏角前左為正，前右為負。由式(1)可知，車輛的運動位置由橫擺角速度、質心速度、質心側偏角決定。由于質心速度自身已包含質心側偏角的信息，因而橫擺角速度與質心速度的變化決定著車輛的運動位置。

1.2 車輛與道路中心線相對位置關系

如圖1所示，大地坐標系XOY中，設車輛前方道路中心線上距離車輛質心橫向距離最近點為Op，即本文所要跟蹤的參考點，其坐標為(Xp，Yp)，其切線方向與橫坐標的夾角為φp。將全局坐標系中車輛與參考點之間的相對位置(Xp-Xc，Yp-Yc，φp-φc)轉化為車輛局部坐標系中的相對位置(xe，ye，φe)，由圖1中的幾何關系可知:

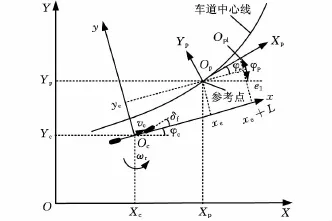
圖1 車輛-道路相對位置

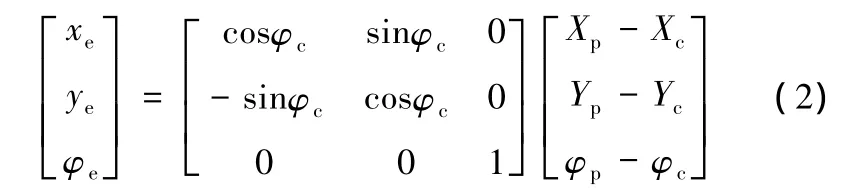
式中，ye、φe分別為車輛局部坐標系中車輛與參考點的橫向距離偏差和方位偏差。

1.3 車輛動力學模型

為了對控制方法進行仿真分析和驗證，需要建立車輛動力學模型來考察車輛在轉向過程中運動狀態與輸入轉向角之間的關系。這里采用二自由度的車輛模型，車輛只具有橫擺運動和側向運動兩個自由度。通過動力學分析，可以得到車輛平面運動的微分方程:

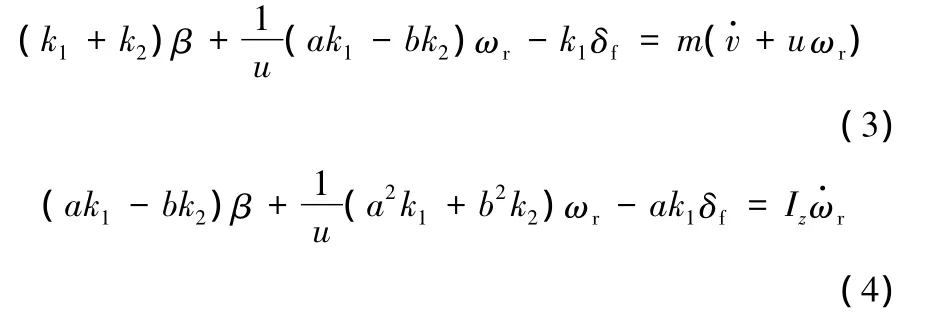
式中，m為整車質量;Iz為繞z軸的轉動慣量;a、b分別為質心到前后軸的距離;u為縱向速度;v為側向速度;k1、k2分別為前后車輪側偏剛度。

把轉向執行機構視為一階慣性環節，可得

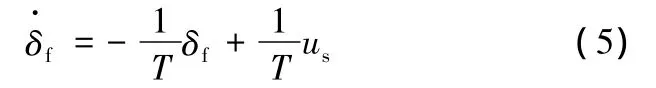
式中，δf為前輪轉角;T為慣性環節時間常數;us為控制輸入。

綜合式(3)～式(5)，可得包含轉向執行機構的車輛系統動力學模型:

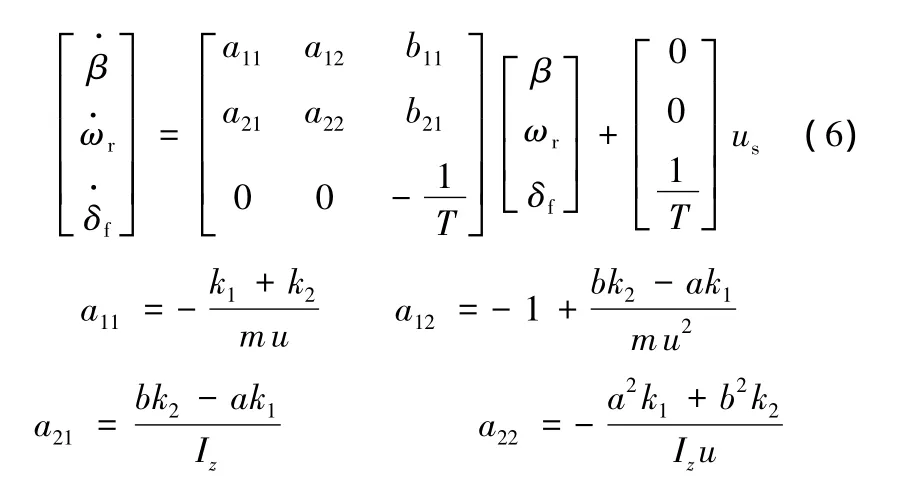
1.4 道路勢場的構建

在利用道路勢場法的路徑跟蹤控制中，其主要原理是考慮車輛控制系統在道路空間不同區域的危險度，該危險度用道路勢場函數表示，控制器根據勢場函數對車輛產生一個恢復力，使車輛自然恢復到具有較低危險度的狀態中。在勢場中同一位置，車輛所受勢場力的大小由勢場函數的增益確定。增大勢場函數波峰相對于波谷的高度能夠產生更大的恢復力。

在路徑跟蹤控制中，一個好的橫向控制響應需要一定量的前瞻信息。因此，本文選擇的道路勢場函數是車輛前方前瞻點處橫向距離偏差e1的函數，如圖2所示。為簡化計算，本文所用勢場函數數學表達式為

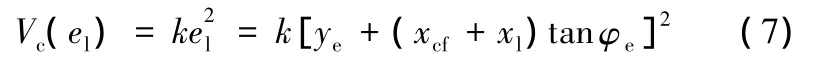
式中，xcf為勢場力在車輛縱軸線上作用位置相對質心的距離;xl為從勢場力作用點起算的前瞻距離;k為勢場函數增益。

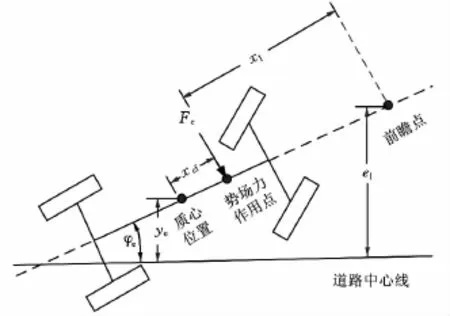
圖2 道路勢場力作用位置圖

一般來說，在勢場函數的選擇中有兩個參數需要考慮［11］:一個是函數的高度，另一個是函數的斜度。勢場函數必須具有一定的勢能，該能量至少能使車輛沿函數梯度方向回到道路中心線，這就決定了勢場函數具體的高度Vc。另一方面，勢場函數的斜度對應于車輛路徑跟蹤控制所需的控制力?Vc/?el。本文中這兩個參數均與勢場函數增益k有關，故在設計勢場函數時主要是尋求適合的勢場函數增益以滿足路徑跟蹤性能要求。根據參考文獻［9］中角度偏差與距離偏差之間的關系，當橫向距離偏差不隨角度偏差變化時k取得最大值，可得

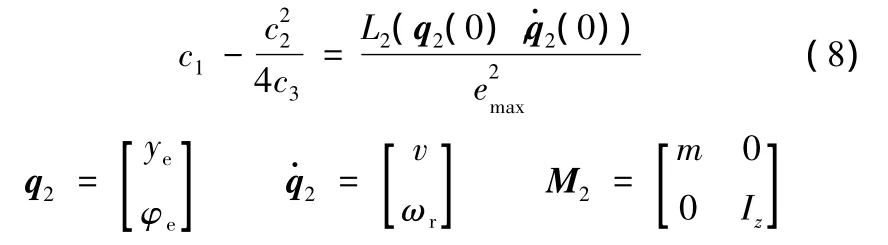
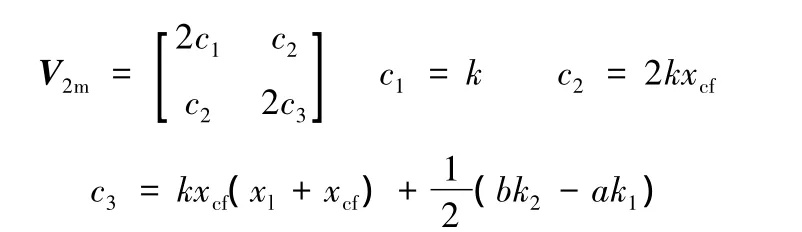
將式(8)展開即可求出在一定容許距離偏差下所要求的k值。

前瞻距離可根據輪胎側偏剛度和勢場函數增益由下式確定［9］:

對于前輪轉向四輪汽車，該控制力對車輛的作用由前輪的偏轉實現，故可取xcf=a，同時能夠保證車輛的穩定性。這里仍假設相對方位偏差φe較小，則道路勢場所產生的控制力為

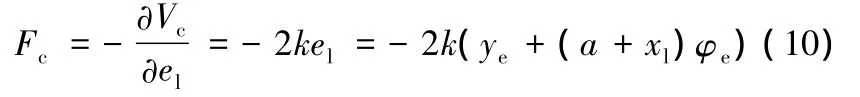
為了減小在路徑跟蹤控制中車輛橫擺運動與側向運動的振蕩，需要對前述勢場力加上橫擺運動阻尼和側向運動阻尼，其阻尼系數分別設為D1、D2。由剛體動力學和汽車在道路平面內的幾何運動特性可得

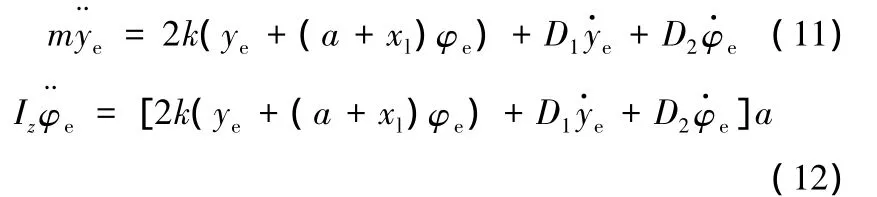
聯立式(11)、式(12)可得如下狀態空間方程:

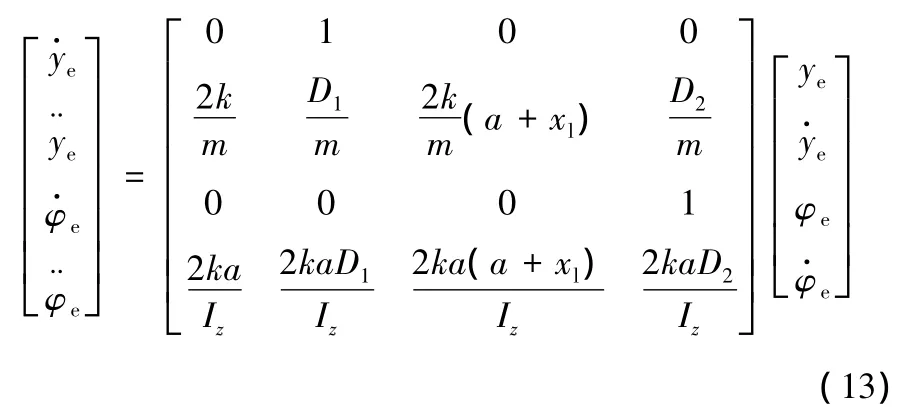
通過配置極點選擇合適的阻尼系數D1=，D2=，可以得到理想的系統響應性能，使偏差快速趨近于零。值得注意的是，為了減小振蕩，阻尼系數應取較大值，而在實際中，阻尼系數往往不能取得太大。因為當系統存在側向或者橫擺速度時，較大的阻尼系數常常會使系統損失能量較多，從而影響跟蹤效率。由此，根據車載傳感系統檢測到的預期行駛軌跡和汽車當前時刻的行駛狀態，利用剛體動力學關系確定汽車的理想側向加速度

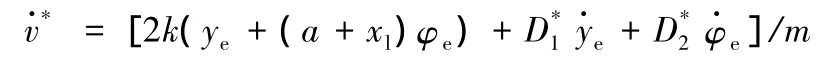
和橫擺角加速度

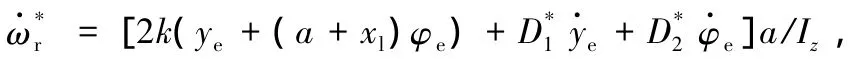
并以此作為控制器的參考輸入信息。

2 道路勢場法路徑跟蹤控制結構

根據“預瞄-跟隨”理論［8］，在得到了理想的側向加速度和橫擺角加速度后，根據汽車側向及橫擺運動動力學特性，建立從理想側向加速度和橫擺角加速度到實際方向盤轉角的控制器，進而將該轉角輸入汽車動力學系統中，得到實際的側向加速度、橫擺角加速度等汽車狀態輸出。

在路徑跟蹤的轉向控制過程中，方向盤轉角采用PID控制。控制器主要通過計算車輛實際側向加速度與理想側向加速度的偏差以及車輛實際橫擺角加速度與理想橫擺角加速度的偏差得到目前方向盤轉角δsw:

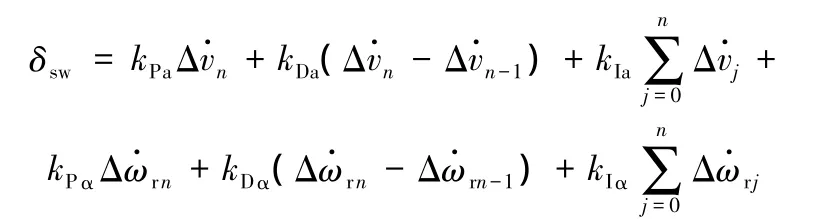
比例、積分和微分環節的各個參數不應是固定不變的，而應該在車輛的實時控制過程中根據控制效果不斷地調整改進，即需要具有一定的自適應能力。采用神經網絡與PID控制相結合的方法，可在線實時整定PID控制器參數，從而提高控制系統的魯棒性和自適應性。基于道路勢場的自適應PID控制流程見圖3。兩組BP神經網絡實現PID控制器的參數自整定計算，即將神經網絡的輸出層神經元的輸出定義為PID控制器的6個可調參數，從而通過BP學習算法調整神經網絡的加權系數，最終找到在誤差最小原則下的PID控制器參數。考慮到傳統BP學習算法收斂速度較慢的缺點，這里采用帶阻尼項的權值調整算法［12］產生足夠大的學習速率，從而保證系統的實時性。

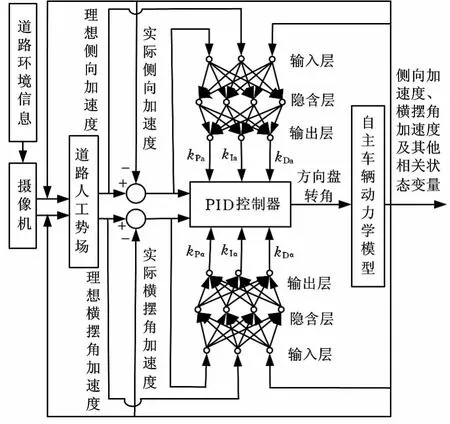
圖3 路徑跟蹤控流程示意框圖

3 仿真結果與分析

為了驗證所提方法的可行性與有效性，在MATLAB/Simulink仿真環境中對上述車輛模型及控制算法進行建模與仿真實驗，道路勢場及車輛的部分參數如表1所示。

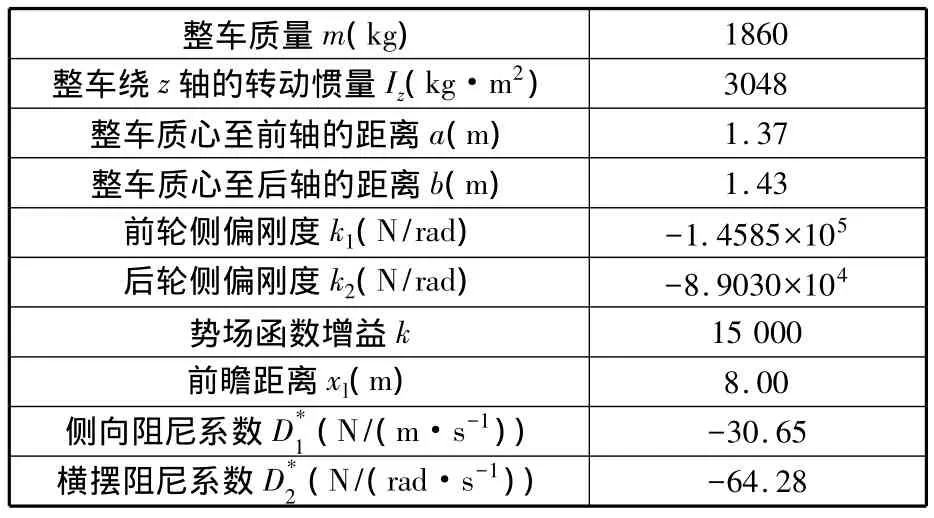
表1 道路勢場及部分車輛參數

仿真過程中為了更好地分析本文提出的控制算法和現有常規位置偏差反饋控制方法［4］的區別，進行了基于道路勢場的路徑跟蹤控制算法和常規位置偏差控制算法的對比仿真，分別進行直線路徑和正弦曲線路徑的跟蹤。車速取20m/s，采樣時間t取0.01s，最大容許跟蹤誤差為1m。直線路徑跟蹤時目標車道中心線方程為Y=0，車輛起始位置坐標為(0，1)，起始方向角為0.5rad;曲線路徑跟蹤時目標車道中心線方程為Y=15［1+sin(X/20)］，車輛起始位置坐標為(30，30)，起始方向角為0.2rad。仿真結果如圖4～圖9所示。

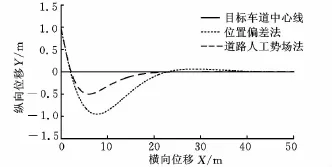
圖4 直線路徑跟蹤軌跡

從兩種控制算法仿真結果的對比曲線可見:道路勢場法通過簡單添加勢場和阻尼函數，協調車輛側向和橫擺運動來消耗總體能量，可以較好地控制汽車跟蹤預期行駛軌跡，體現出良好的車輛側向運動控制的軌跡跟隨性能，直線跟蹤與曲線跟蹤的誤差(即距離偏差Δd=Yp-Yc和角度偏差Δφ=φp-φc)及控制超調均比位置偏差反饋法要小。這是由于位置偏差反饋相比于車輛狀態反饋存在時間滯后;勢場法同時考慮了側向加速度和橫擺角加速度的影響。比如在車輛跟蹤曲線路徑上彎曲度較大的路段時，即便車輛與參考點處距離偏差很小，但車輛與參考點的角度偏差仍然很大。同時本文控制算法所采用的BP神經網絡自適應PID控制算法能夠根據車輛行駛狀態速度的變化以及預期行駛軌跡的變化在線調整PID控制器的參數，因而具有較強的魯棒性和適應性。

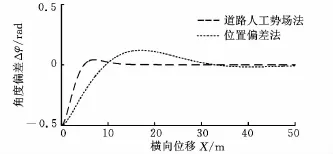
圖5 直線路徑跟蹤時角度偏差

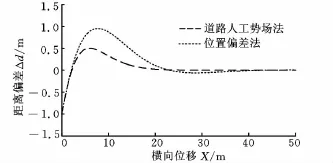
圖6 直線路徑跟蹤時距離偏差

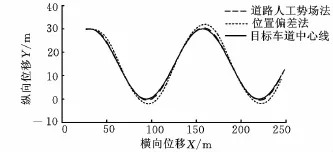
圖7 曲線路徑跟蹤軌跡

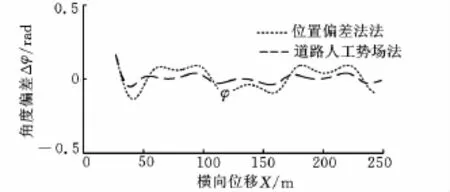
圖8 曲線路經跟蹤時角度偏差

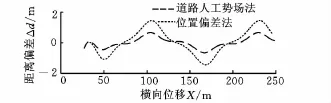
圖9 曲線路徑跟蹤時距離偏差

4 試驗驗證

理論上，利用道路勢場產生控制器參考輸入信息的路徑跟蹤控制方法能夠有效地完成任務。為驗證該方法在實車上的實用性，對其進行了試驗驗證。

4.1 試驗平臺

試驗車輛由前輪轉向后輪驅動的四輪電動車改裝而成，如圖10所示。車輛根據攝像機等環境感知傳感器獲取前方道路信息;利用其視覺車道識別系統，根據這些信息實時計算出車輛前方期望路徑(即車道中心線)，并確定車輛自身位置與方向。

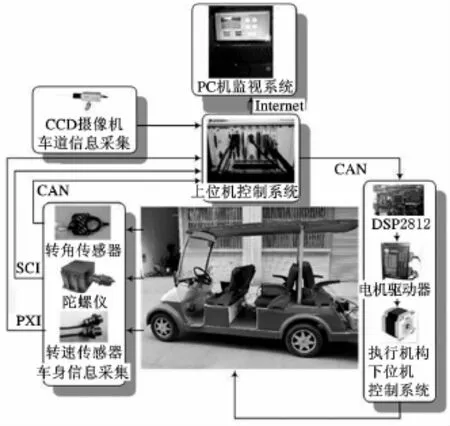
圖10 路徑跟蹤試驗平臺

采用LabVIEW PXI8196作為上位機負責道路圖像及車身傳感器信號中方向盤轉角、橫擺角速度、側向加速度、縱向車速的采集。同時，在上位機中實現車道識別算法和路徑跟蹤控制算法，車道識別模塊將計算出的車輛與參考點相對位置作為道路勢場決策模塊的輸入。TI公司DSP2812作為下位機接收控制指令并轉換成PWM脈沖控制電機實現前輪轉向，自動轉向系統通過步進電機驅動轉向軸實現，車速自動控制系統通過控制驅動電機實現。PC機實時監視車身傳感器及車輛道路相對位置信息。所有的設備實現車載，設備所需電力由蓄電池及逆變器提供。

試驗中，路徑跟蹤的道路勢場函數取與前述仿真分析中一樣的二次函數以及相關參數。

4.2 試驗結果與分析

試驗時，縱向車速控制系統控制縱向車速保持恒定，分別采用位置偏差反饋法和道路勢場法進行路徑跟蹤實車試驗。試驗中車輛與目標路徑的偏差數據由上位機LabVIEW PXI8196識別車道時在圖像中實時記錄，再根據攝像機采集圖像過程中三角形相似的原理及坐標系變換計算出來。試驗場地包含直線路徑和彎曲路徑。

在車速為5m/s、距離偏差為0.5m、角度偏差為0.25rad的條件下跟蹤直線路徑，采用位置偏差反饋法和道路勢場法控制車輛達到穩定跟蹤狀態的平均時間分別為2.64s和1.35s。可見，在相同條件下本文方法能夠更及時地控制車輛回到目標路徑上。

表2所示為采用上述兩種方法在不同車速下進行路徑跟蹤時車輛與目標路徑之間距離偏差數據，顯示了車輛在車道偏離時兩種方法的總體跟蹤性能。從表2中數據可以看出，采用位置偏差反饋法跟蹤時比道路勢場法的偏差明顯增大，而本文方法主要是在跟蹤過程中同時考慮了側向和橫擺運動的控制，使得車輛在跟蹤路徑時有更好的效果。同時還可以看出，隨著車速的提高，兩種控制方法的偏差均增大，這主要是由于改裝的試驗車輛轉向電機控制機構存在響應滯后。

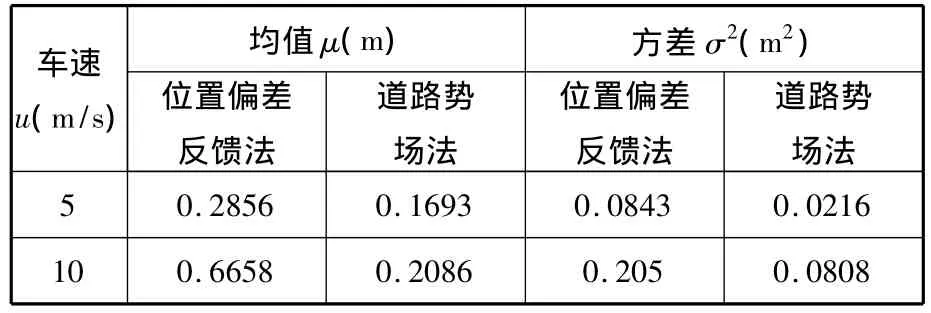
表2 路徑跟蹤距離偏差

［1］Li L，Wang F.Advanced Motion Control and Sensing for Intelligent Vehicles［M］.Berlin:Springer，2007.

［2］Hernandez J I，Kuo C.Steering Control of Automated Vehicles Using Absolute Positioning GPS and Magnetic Markers［J］.IEEE Transactions on Vehicular Technology，2003，52(1):150-161.

［3］趙熙俊，陳慧巖.智能車輛路徑跟蹤橫向控制方法的研究［J］.汽車工程，2011，5(33):382-387.Zhao Xijun，Chen Huiyan.A Study on Lateral Control Method for the Path Tracking of Intelligent Vehicles［J］.Automotive Engineering，2011，5(33):382-387.

［4］陳無畏，李進，王檀彬，等.視覺導航智能車輛的路徑跟蹤預瞄控制［J］.機械工程學報，2008，44(10):277-282.Chen Wuwei，Li Jin，Wang Tanbin，et al.Preview Control for Road Following of Vision Guided Intelligent Vehicle［J］.Journal of Mechanical Engineering，2008，44(10):277-282.

［5］游峰，王榮本，張榮輝，等.智能車輛換道與超車軌跡跟蹤控制［J］.農業機械學報，2008，6(11):42-45.You Feng，Wang Rongben，Zhang Ronghui，et al.Lane Changing and Overtaking Control Method for Intelligent Vehicle Based on Backstepping Algorithm［J］.Transactions of the Chinese Society for Agricultural Machinery，2008，6(11):42-45.

［6］Wang J，Steiber J，Surampudi B.Autonomous Ground Vehicle Control System for High-speed and Safe Operation［J］.International Journal of Vehicle Autonomous Systems，2009，7(1/2):18-35.

［7］王家恩，陳無畏，王檀彬，等.基于期望橫擺角速度的視覺導航智能車輛橫向控制［J］.機械工程學報，2012，48(4):108-115.Wang Jiaen，Chen Wuwei，Wang Tanbin，et al.Vision Guided Intelligent Vehicle Lateral Control Based on Desired Yaw Rate［J］.Journal of Mechnical Engneering，2012，48(4):108-115.

［8］高振海.汽車方向預瞄式自適應PD控制算法［J］.機械工程學報，2004，40(5):101-105.Gao Zhenhai.Vehicle Direction Preview Adaptive PD Control Algorithm［J］.Journal of Mechnical Engneering，2004，40(5):101-105.

［9］Rossetter E J，Gerdes J C.Lyapunov Based Performance Guarantees for the Potential Field Lane-keeping Assistance System［J］.Journal of Dynamic Systems Measurement and Control，2006，128(3):510-522.

［10］Brandt T，Sattel T，Wallaschek J.Towards Vehicle Trajectory Planning for Collision Avoidance Based on Elastic Bands［J］.International Journal of Vehicle Autonomous Systems，2007，5(1):28-46.

［11］Rossetter E J.A Potential Field Framework for Active Vehicle Lanekeeping Assistance［D］.Stanford:Stanford University，2003.

［12］高振海，姜立勇.汽車車道保持系統的BP神經網絡控制［J］.中國機械工程，2005，16(3):272-277.Gao Zhenhai，Jiang Liyong.Vehicle Lane Keeping System Control with BP Neural Network［J］.China Mechanical Engineering，2005，16(3):272-277.