新型灰關聯分析方法研究及其在數控機床主軸故障識別中的應用

楊東升 李紅衛，2 孫一蘭 尹震宇

1.中國科學院沈陽計算技術研究所，沈陽，110171 2.中國科學院研究生院，北京，100039

0 引言

故障識別是一種利用設備當前狀態信息和歷史狀況，采用一定分析方法對設備狀態進行評價的狀態識別技術。在設備運行過程中，故障與征兆之間沒有確定的映射關系，因此可以將設備看作是一個復雜的灰色系統。

灰色系統理論作為一種處理非確定性問題的方法，由鄧聚龍［1］于20世紀80年代提出，經過多年發展，該理論已應用于預測、線性規劃、系統控制等領域［2-4］。灰關聯分析方法作為灰色理論的一個重要組成部分，目前在故障識別領域被廣泛應用［5-6］，并取得了良好效果。但是，這種傳統灰關聯分析方法存在以下問題:①關聯度值受分辨系數影響而不唯一;②關聯度值離散性不強，結果趨于均化且可靠性低;③忽略了因子權重差異。

在傳統灰關聯分析方法的基礎上，本文引入動態關聯系數和因子權重系數，提出了新型灰關聯分析方法，有效地解決了以上問題，將其運用于數控機床主軸故障識別中，提高了識別結果的可靠性和準確性，為數控機床及主軸生產廠家提供了良好的故障識別方法。

1 傳統灰關聯分析方法及其存在的問題

灰關聯分析是事物間不確定關系的量化分析，灰關聯度是一種數據到數據的“映射”，代表了不同研究對象之間的關聯程度。

1.1 傳統灰關聯分析方法基礎

設兩組向量，一組為比較向量，記為Xi=(Xi(1)，Xi(2)，…，Xi(N))(i=1，2，…，m);一組為 參 考 向 量， 記 為 Yj=(Yj(1)，Yj(2)，…，Yj(N))(j=1，2，…，n)。Xi(k)和Yj(k)分別為Xi和Yj的第k個特征分量，其中k=1，2，…，N。傳統灰關聯分析過程如下:

(1)計算比較向量Xi與參考向量Yj在k點的關聯系數ξij(k):

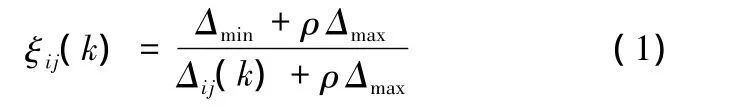
式中，ρ為分辨系數，傳統灰關聯分析中通常設為0.5。

(2)計算比較向量Xi與參考向量Yj的關聯度γij:

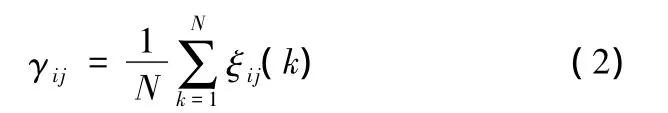
1.2 傳統灰關聯分析方法存在的問題

由式(1)、式(2)容易看出傳統灰關聯分析方法存在以下問題:

(1)關聯系數ξij取值受分辨系數ρ不同取值的影響，導致關聯度γij具有不唯一性。

(2)分辨系數ρ影響關聯度分布區間，人為主觀設置ρ=0.5將導致結果趨于均化，降低區分度。

(3)忽略不同因子權重差異，與工程實際應用不符。

2 新型灰關聯分析方法

為解決1.2節中的問題，本文以傳統灰關聯分析方法為基礎，在式(1)和式(2)中分別引入動態分辨系數和權重系數，形成新型灰關聯分析方法。

2.1 動態分辨系數的確定［7］

定義1:比較向量Xi與所有參考向量Yj差值絕對值的均值為

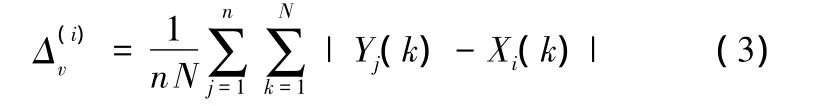
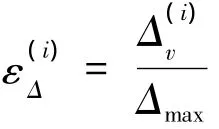
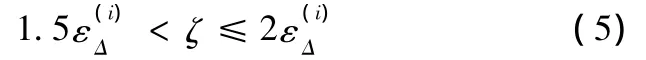
按上述方法動態選取ζ值，不僅使分辨系數取值具有一定的客觀基礎，而且有一定的智能性和靈活性。用動態分辨系數ζ替換式(1)中的靜態分辨系數ρ，得到具有動態分辨系數的關聯系數ξ'ij的計算公式:

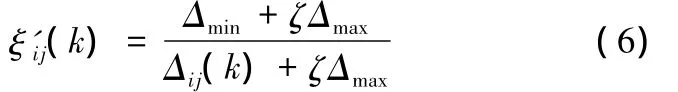
2.2 加權系數的確定［8］

定義3:設序列 Yj(k)={Yj(1)，Yj(2)，…，Yj(k)，…，Yj(N)}(j=1，2，…，n;k=1，2，…，N)，各序列中各屬性因子總和為

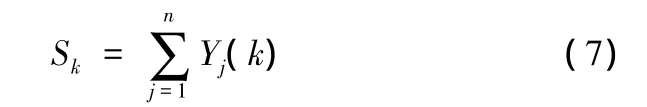
定義4:設一函數映射為f(x)=xe1－x+(1－x)ex－ 1，稱函數

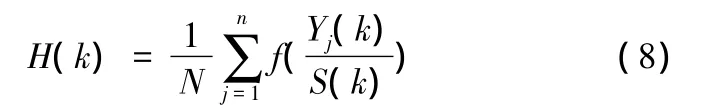
為因子k的熵。

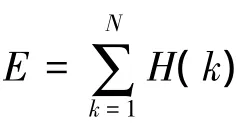
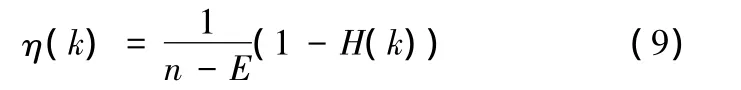
為因子k的相對權重。

定義6:若w為相對權重和，稱函數

為因子k的權重。

式(2)取加權系數，結合式(6)，即可得到新的關聯度計算公式:

式(6)和式(11)即是本文提出的新型灰關聯分析方法。與傳統灰關聯分析方法相比，該方法具有以下優點:

(1)不依賴于人為確定的分辨系數ρ，而是根據比較向量和參考向量動態計算分辨系數ζ，當比較向量和參考向量一定時，關聯度值唯一。

(2)動態分辨系數ζ減少了人為主觀因素對關聯度分布區間的影響。

(3)賦予不同因子不同的權重，更能反映不同因子具有不同作用和地位的實際情況。

3 實例、結果及分析

3.1 診斷對象

本文所討論的識別對象為數控機床主軸零件松動(F1)、配合松動(F2)和動不平衡(F3)三種狀態。利用新型灰關聯分析方法對其進行故障識別的原理如圖1所示。

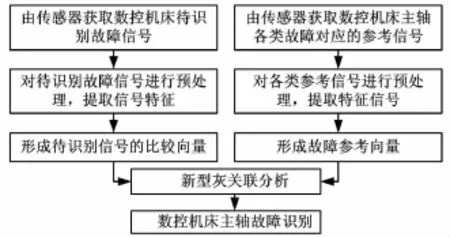
圖1 新型灰關聯分析故障識別原理圖

本文分析的基礎是文獻［9］中有關數控機床主軸的振動信號，這些振動信號反映了數控機床主軸的三種狀態，通過傅里葉變換進行頻譜分析，可得到特定狀態下的頻譜特征。數控機床主軸故障機理分析及不同狀態下的頻譜圖表明，不同狀態對應不同的頻譜特征，主要表現在頻譜圖中0.4～0.5倍頻(f1)、1倍頻(f2)、2 倍頻(f3)、3倍頻(f4)和大于3倍頻(f5)的特征頻段振幅不同。以F1狀態振動信號為例，其頻譜圖如圖2所示。因此，本文分析時將這5個特征頻段振幅作為特征值。為更好地進行關聯分析和故障識別，對特征值進行歸一化處理，以得到識別需要的特征值:

其中，fk為每組原始數據中第k個特征值的取值，k=1，2，…，5。

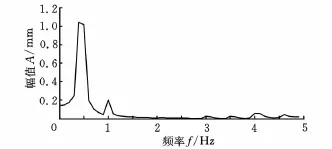
圖2 F1狀態振動信號頻譜圖

為進行分析，針對每種狀態，本文采用5組振動信號(每組包含100個數據)，經傅里葉分析，得到特定狀態下的5組特征值，歸一化后，構成對應于三種狀態的15組特征值(1～5對應于狀態F1，6～10對應于狀態 F2，11～15對應于狀態F3)，如表1所示。

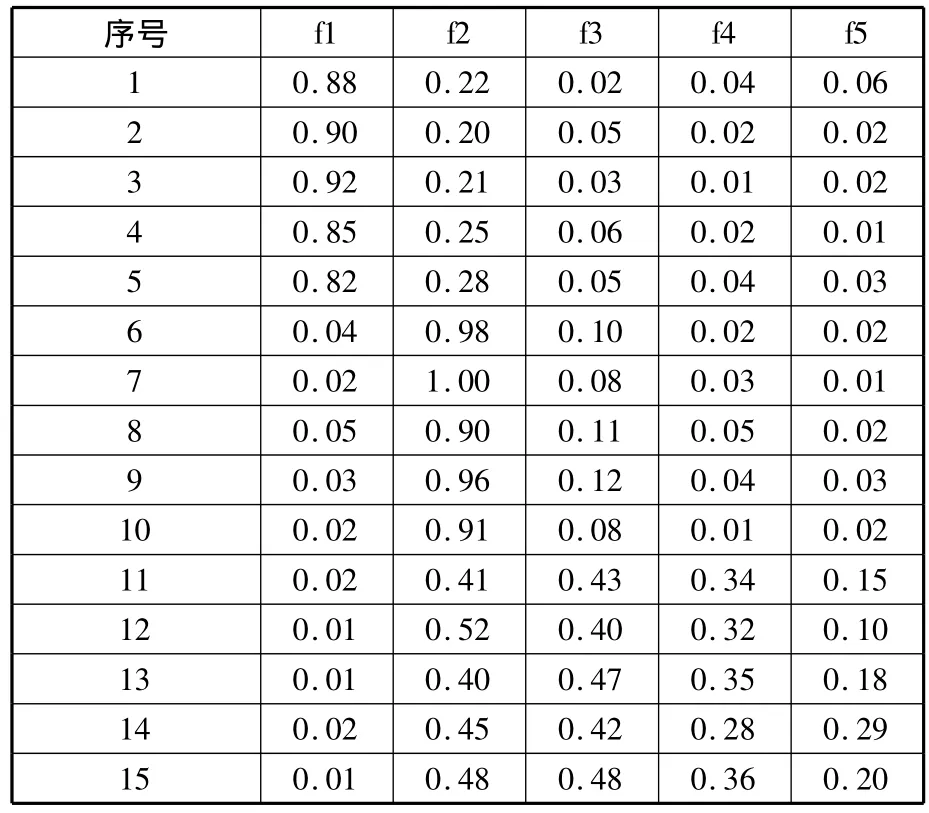
表1 故障信號特征值表 cm

3.2 參考向量與比較向量的構造

選取表1中序號為1、6和11的行作為參考向量，形式為(Y1，Y2，Y3)T，其中Yj=(Yj(1)，Yj(2)，Yj(3)，Yj(4)，Yj(5))(j=1，2，3)。j=1 時，代表數控機床主軸處于F1狀態;j=2時，代表數控機床主軸處于F2狀態;j=3時，代表數控機床主軸處于F3狀態。實際應用中，參考向量的選取影響識別結果的準確性和可靠性，可視特定故障狀態下的所有特征值平均值為參考向量;另外，也可將所有特征值均作為參考向量，故障識別時，比較向量與每個參考向量進行新型灰關聯分析，將得到的多個識別結果進行綜合處理，可使識別結果更準確可靠。

選取表1中除序號為1、6和11之外的其他所有行作為比較向量，形式為(X1，X2，…，X12)T，其中 Xi=(Xi(1)，Xi(2)，Xi(3)，Xi(4)，Xi(5))(i=1，2，…，12)，該組向量用來驗證本文方法是否有效，其中，X1～X4為數控機床主軸F1特征信號;X5～X8為數控機床主軸F2特征信號;X9～X12為數控機床主軸F3特征信號。實際應用中，運行過程中獲取的每一特征值均可作為比較向量。

3.3 故障識別及結果分析

3.3.1識別結果

根據2.1節和2.2節給出的方法，進行新型灰關聯分析，得到參考向量各因子權重和狀態識別結果，分別如表2和表3所示。表3中，ζ列表示特定比較向量對應的動態分辨系數;關聯度列表示比較向量與各參考向量的關聯強度，關聯度值越大，表示關聯程度越緊密。本文中，選取關聯度值最大者為比較向量對應的故障狀態。

表2 參考向量因子權重

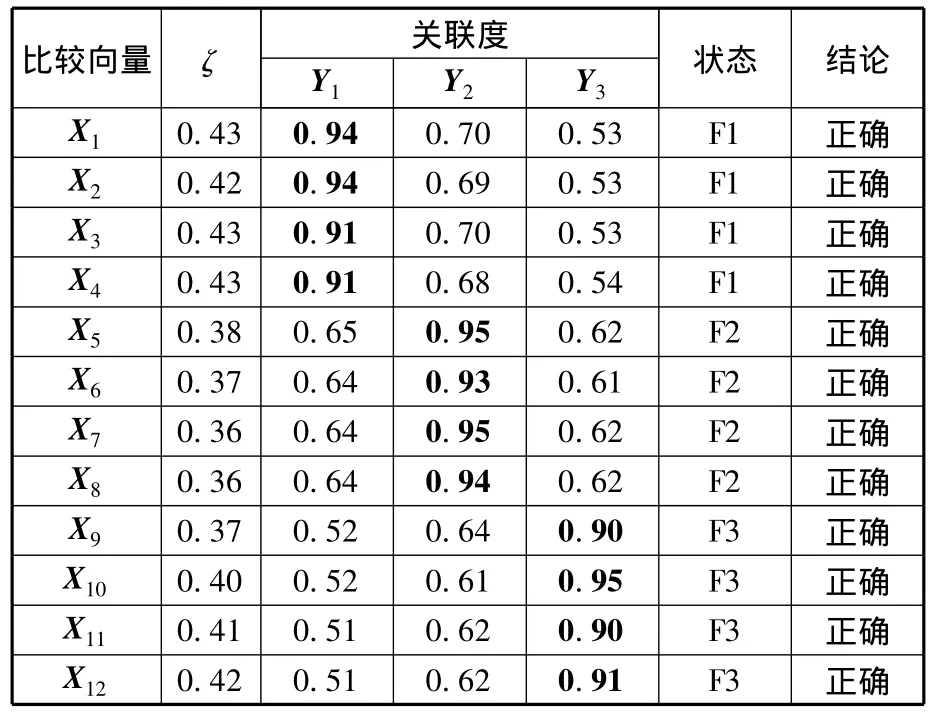
表3 新型灰關聯分析識別結果

從表3可得出以下結論:①新型灰關聯分析方法可有效地識別數控機床主軸的三種狀態;②比較向量所屬故障狀態對應的關聯度值分量與其他分量的距離較大，識別結果可靠。

3.3.2對比分析

為進一步對新型灰關聯分析方法進行討論，本文將該方法識別結果與傳統灰關聯分析方法識別結果進行對比分析。另外，由于數控機床主軸故障特征參考向量難于獲取，在少量參考向量情況下得到更為準確的識別結果在數控機床主軸故障識別中尤為重要，因此，本文還將該新型關聯分析方法與神經網絡識別結果進行對比分析。

(1)與傳統灰關聯分析方法的比較。傳統灰關聯分析方法計算過程所需數據與上述新型灰關聯分析方法所使用的數據一致，根據1.1節介紹的傳統灰關聯分析計算方法，得到傳統灰關聯分析方法的識別結果，如表4所示。

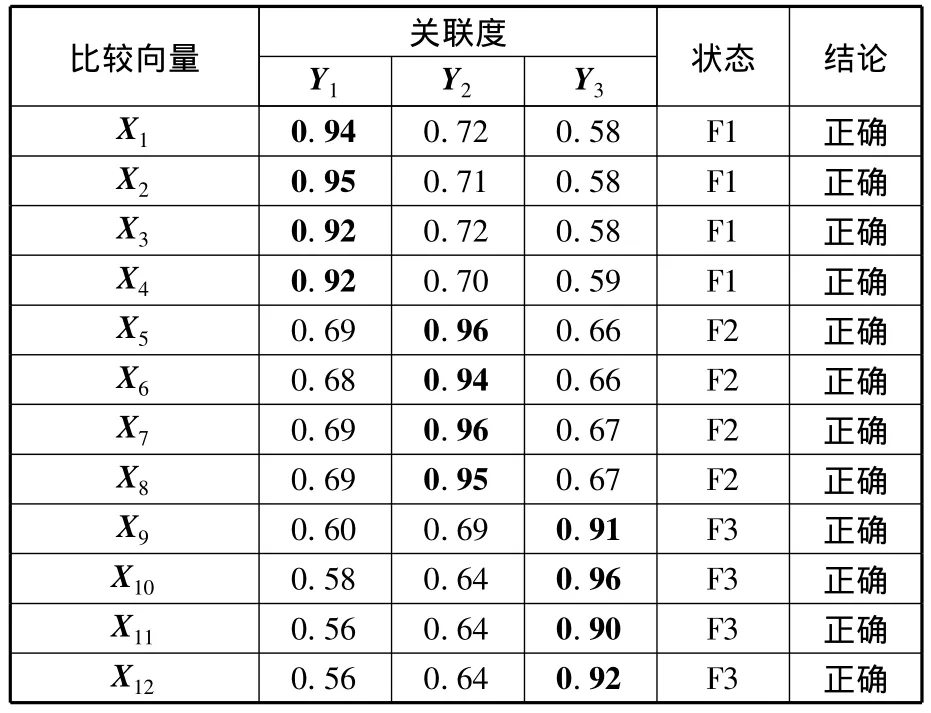
表4 傳統灰關聯分析方法識別結果(ρ=0.5)

表4表明，傳統灰關聯分析方法也可有效地識別數控機床主軸的三種狀態。關聯度離散性表示關聯度之間的安全隔離空間，關聯度離散性越大，表示識別結果區分度越大，可靠性越高。現從關聯度離散性方面對表3和表4進行分析，如圖3所示。圖3表明新型灰關聯分析方法使關聯度離散性增大，可有效避免因外界干擾或數據波動導致的識別錯誤，提高了識別結果的可靠性。

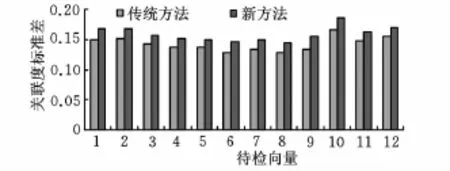
圖3 關聯度標準差對比圖

(2)與神經網絡的比較。將表1中序號為1、6和11的行作為BP神經網絡的訓練樣本，其他行作為驗證的比較向量。在總體學習誤差分別為0.05、0.1和0.15時訓練網絡，得到在每種訓練模式下的識別誤差，求三種誤差的平均值，并與新型灰關聯分析方法識別誤差進行對比，如圖4所示。

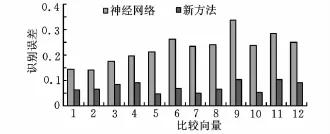
圖4 結果識別誤差對比圖

圖4表明，在單樣本情況下，相對于神經網絡，新型灰關聯分析方法可有效減小識別誤差，提高識別結果的準確性，這說明新型灰關聯分析方法比神經網絡更適于經驗樣本數據少的故障識別場合。另外，在實驗過程中發現，神經網絡識別誤差隨總體學習誤差的減小而減小，但總體學習誤差的減小將導致訓練步數增加，訓練時間變長;此外，樣本發生變化時，神經網絡需重新進行訓練，診斷效率降低。新型灰關聯分析方法與其相比，計算量小，不需訓練，過程簡單，更適于有實時故障識別要求的場合。

4 結語

本文在分析傳統灰關聯分析方法及其存在問題的基礎上，引入動態分辨系數和權重系數，提出了新型灰關聯分析方法，減少了人為干預，提高了灰關聯分析的可靠性和準確性。在此基礎上，將該方法應用于數控機床主軸故障識別，取得了良好效果，同時給出了該方法識別結果與傳統灰關聯分析方法和神經網絡識別結果的對比分析，證明了該方法的優越性。另外，這種新型灰關聯分析方法屬于廣義的灰關聯分析方法，可廣泛應用于其他故障和信號識別領域，具有良好的實際應用價值。

［1］鄧聚龍.灰色系統理論教程［M］.武漢:華中理工大學出版社，1990.

［2］Wang M H.Grey－extension Method for Incipient Fault Forecasting of Oil－immersed Power Transformer［J］.Electric Power Components and Systems，2004，32(10):959-975.

［3］趙磊，李原，余劍峰.支持變約束的裝配順序隨需式規劃方法［J］.機械工程學報，2011，47(5):149-155.Zhao Lei，Li Yuan，Yu Jianfeng.Assembly Sequence Concomitant Planning Method Based for the Variation［J］.Journal of Mechanical Engineering，2011，47(5):149-155.

［4］辛民，王西彬，解麗靜，等.基于灰色理論的銑削參數優化方法研究［J］.中國機械工程，2009，20(23):2807-2810.Xin Min，Wang Xibin，Xie Lijing，et al.Study on Milling Parameter Optimization Method Based on Gray Theory［J］.China Mechanical Engineering，2009，20(23):2807-2810.

［5］劉軍，盧炎生.一種粗集與灰色理論結合算法在柴油機故障診斷系統中的應用［J］.小型微型計算機系統，2010，31(4):797-800.Liu Jun，Lu Yansheng.Application of One Combined Algorithm in Diesel Engine Fault Diagnosis System Based on Rough Set and Grey Theory［J］.Journal of Chinese Computer System，2010，31(4):797-800.

［6］Jiang Lingping.Gas Path Fault Diagnosis System of Aero－engine Based on Grey Relationship Degree［J］.Procedia Engineering，2011，15:4774-4779.

［7］東亞斌，段志善.灰色關聯度分辨系數的一種新的確定方法［J］.西安建筑科技大學學報(自然科學版)，2008，40(4):589-592.Dong Yabin，Duan Zhishan.A New Determination Method for Identification Coefficient of Grey Relational Grade［J］.Journal of Xi’an University of Arch.＆Tech.(Natural Science Edition)，2008，40(4):589-592.

［8］羅佑新，張龍挺，李敏.灰色系統理論及其在機械工程中的應用［M］.長沙:國防科技大學出版社，2001.

［9］吳今培，肖健華.智能故障診斷與專家系統［M］.北京:科學出版社，1997.