基于改進PSO算法的PID控制器研究

?

基于改進PSO算法的PID控制器研究

張燕紅

（常州工學院電子信息與電氣工程學院，江蘇常州213002）

摘要：針對一般的粒子群優化（PSO）學習算法中存在的容易陷入局部最優和搜索精度不高的缺點，對改進型PSO算法進行研究。由于慣性權重系數ω對算法是否會陷入局部最優起到關鍵的作用，因此，通過改變慣性權重ω的選擇，對慣性權重系數采取線性減小的方法，引入改進型的PSO算法。采用改進的PSO算法對PID控制器進行參數優化并把得到的最優參數應用于控制系統中進行仿真。仿真實驗結果表明：改進型PSO算法不會陷入局部最優，能得到全局最優的PID控制器的參數，并使得控制系統的性能指標達到最優，控制系統具有較好的魯棒性。

關鍵詞：粒子群優化算法；控制器；參數優化；性能指標；魯棒性

收到修改稿日期：2012-12-27

0　引言

多年來，由于PID控制器的結構簡單，設計方法非常成熟，對線性控制系統有很好的控制效果，因此，PID控制器一直是工業控制系統中應用最廣泛的控制器，PID控制器對大多數的簡單工業過程都能得到滿意的效果[1-3]。但是當控制系統比較復雜或者被控對象的模型發生變化或者由于擾動信號的影響使得系統的穩定性和動態性能受到影響時，之前固定的PID控制器的3個比例、積分和微分參數就很難滿足系統的要求了，因此在PID控制器的應用中，3個參數的調整和優化問題一直是PID控制器研究的熱點問題[4-5]，近年來，不少學者研究了很多優化算法[6]。

本文結合先進控制策略和智能控制算法，采用改進型的PSO優化算法，對PID控制器的參數進行優化，尋優出來的3個參數應用于控制系統中，使得之前不穩定的控制系統具有很好的魯棒性。

1　改進型PSO算法

粒子群優化算法（PSO）是由Jim Kennedy和Eberhart于1995年提出的。它是源于對鳥群捕食行為的研究，一群鳥在隨機搜尋食物，如果這個區域里只有一塊食物，那么找到食物的最簡單有效的策略就是搜尋目前距離食物最近的鳥的周圍區域，PSO算法就是從這種模型中得到啟示而產生的，并用于解決優化問題[7]。在粒子群算法中，每個個體稱為一個“粒子”，每個粒子代表一個潛在的解。所有的粒子都有一個由被優化的函數決定的適應度值，每個粒子還有一個速度決定它們飛翔的方向和距離，群體在解空間中追隨最優粒子進行搜索。粒子通過事先設定的適應值函數（目標函數），計算當前的適應值，根據適應值是否達到最優來衡量粒子位置的優劣。在每一次迭代中，粒子通過跟蹤兩個極值來更新自己，第一個就是粒子自己找到的最優解，稱為個體極值；另一個則是整個粒子群目前找到的最優解，稱為全局極值。PSO首先隨機初始化為一群粒子，在迭代過程中，粒子通過跟蹤前面粒子最優的個體極值點和全局極值點來更新自己當前的位置和速度[8]。由于PSO算法具有簡單易于實現的優點，被越來越多地應用于函數優化、神經網絡訓練、模式分類以及傳統優化算法的應用領域。PSO算法的收斂速度比較快，但是容易陷入局部最優，這與慣性權重系數ω的選擇有關。根據經驗，慣性權重系數ω越大，粒子尋優的全局性越好，ω越小越有利于算法收斂。因此，在尋優的開始階段，希望比較大的慣性因子ω使得尋優的范圍比較廣；在尋優的最后階段，希望較小的慣性因子ω使得算法具有較好的收斂性；因此，本文通過把一般PSO算法中的固定慣性因子ω改變為線性變化的慣性因子ω，而且是隨著迭代次數的增加線性減小的，這樣更好地兼顧了算法的尋優問題和收斂性問題[9-10]。

假設由n個粒子組成的種群p=（p1，p2，…，pn），其中第i個粒子的位置為pi=（pi1，pi2，…，pin），速度為νi=（νi1，νi2，…，νin），位置和速度更新公式為

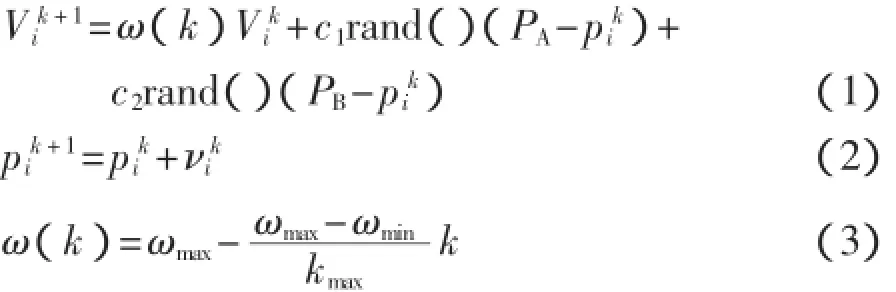
2　改進型PSO控制算法的流程圖

改進型PSO的流程圖如圖1所示。

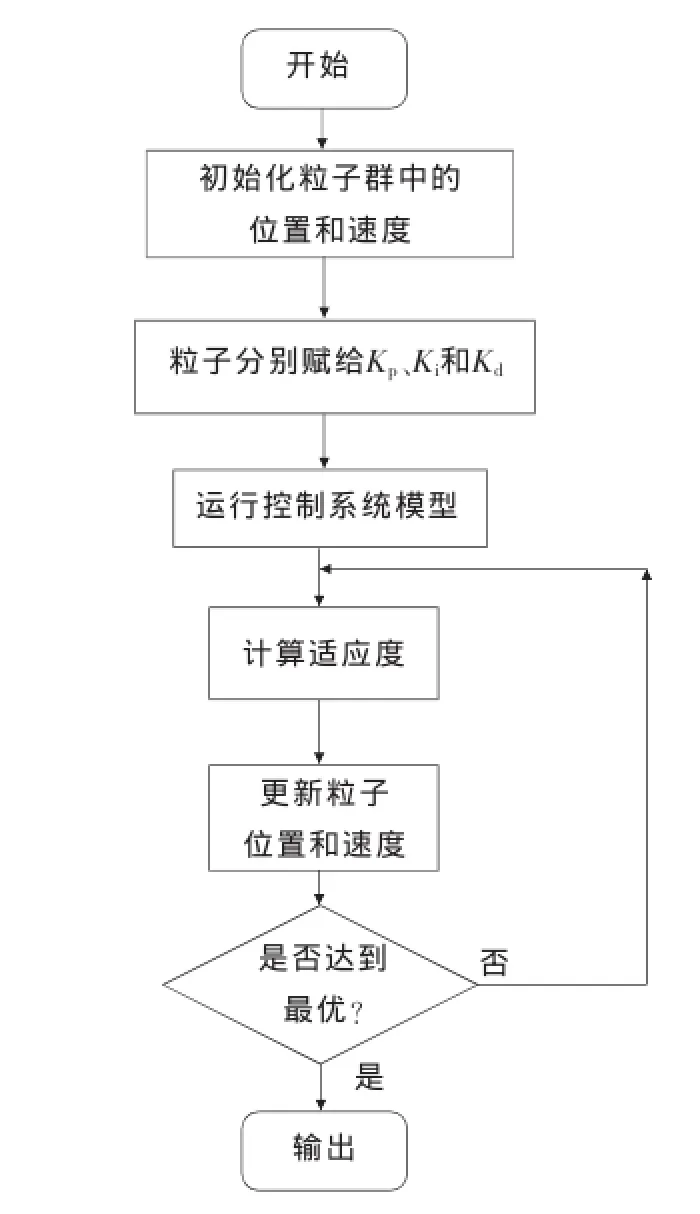
圖1　改進型PSO算法的流程圖

（1）初始化粒子群的各種參數，隨機產生所有粒子的位置和速度，并確定粒子的最優位置和整個粒子群的最優位置。

（2）對粒子群中的每個粒子，將它的適應值（目標函數值）與該粒子所經歷過的最優位置的適應值相比較，如果較好，則將其作為當前的最優位置；否則保留原來粒子的位置作為最優位置。

（3）對粒子群中的每個粒子，將它的適應值（目標函數值）與整個粒子群所經歷過的最優位置的適應值相比較，如果較好，則將其作為當前的粒子群的最優位置；否則保留原來粒子群的位置作為最優位置。

（4）更新粒子的位置和速度。

（5）如果沒有滿足終止的條件，則返回步驟（2）；否則，退出算法，得到最優解。

3　基于改進型PSO算法的控制系統仿真

在Simulink環境下建立PID控制系統的模型，如圖2所示。其中被控對象的傳遞函數為

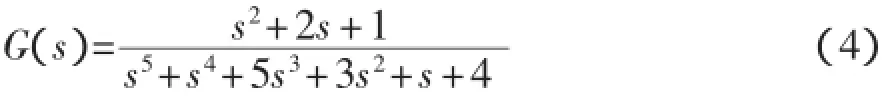
該系統是一個不穩定的控制系統，PID控制器

乙∞采用的是不完全微分，采用的性能指標為J=0e（2t）。設置改進的PSO的初始參數為：粒子群的規模為200，加速常數為c1=2，c2=3，速度的范圍為[-1，1] ，待優化參數的個數為3個，即PID控制器中的3個參數kp、ki和kd，被優化參數的范圍為[0，100] ，慣性權重系數ω1=0.9，ω2=0.4，最大迭代次數為50，分別采用一般的PSO算法和改進型的PSO算法進行尋優。改進型PSO算法的控制系統得到的最優個體適應值變化曲線如圖3所示，PID控制器的3個參數kp、ki和kd的變化曲線如圖4所示。把圖4得到的PID控制器的3個參數代入圖2的控制系統的仿真模型中，輸入信號采用單位階躍信號，在PID控制器的最優參數的狀況下，對控制系統進行仿真，得到的控制系統的輸出曲線如圖5（a）所示，改進前PSO算法的控制系統的輸出曲線如圖5（b）所示。

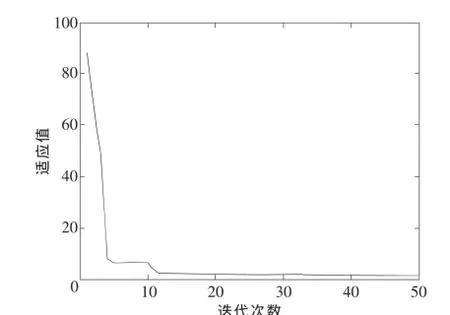
圖3　最優個體適應值的變化曲線

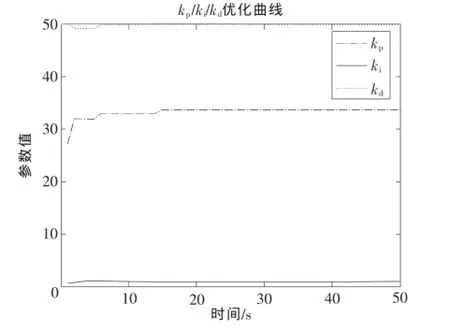
圖4　PID參數的優化曲線

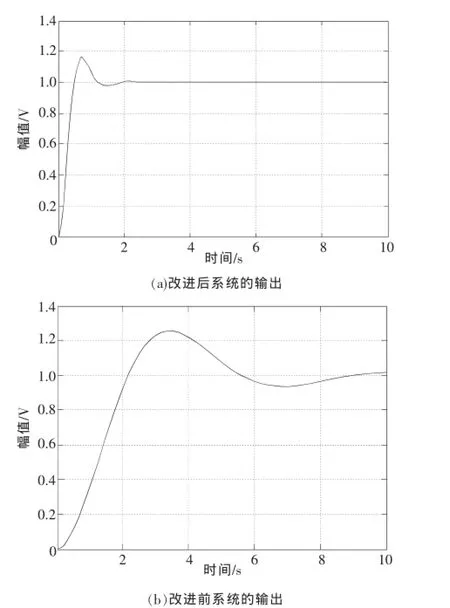
圖5　控制系統在最優參數狀態下的輸出曲線

從圖3可以看出，最優個體適應值在迭代次數為33次的時候趨于0，說明系統存在的穩態誤差e（t）基本趨于0，系統具有很好的穩態性和穩態精度。從圖4中看出經過20次迭代后，尋出的最優的PID控制器的參數為：kp=34，ki=0.2，kd=50。把最優的PID控制器的參數帶入控制系統中進行系統仿真，從圖5可以看出，采用改進型的PSO算法后，控制系統的輸出的超調量為17%，上升時間tr=0.45 s，峰值時間為tp=0.7s，調節時間ts=1s，而一般PSO算法的控制系統的輸出的超調量為23%，上升時間tr=2.1s，峰值時間為tp=2.8s，調節時間ts=7.8s。

從性能指標上看，采用改進型的PSO算法的控制系統具有很好的快速性、平穩性和穩態精度，采用改進型PSO算法提高了控制系統的穩態性能和動態性能。

4　結束語

針對一般的粒子群算法中固定慣性系數ω的大小對粒子尋優的范圍的影響，慣性系數ω越大，粒子尋優的全局性越好，ω越小更利于算法收斂。本文通過對粒子群優化算法中慣性系數的改進，提出了新的改進型粒子群優化算法，使得慣性系數ω線性減小，前期的時候慣性系數ω有利于粒子的全局尋優，后期的時候慣性系數ω有利于PSO算法的收斂。把改進型PSO算法應用于PID控制器中，對PID控制器的3個參數進行尋優，得到kp、ki和kd的最優值，把尋出的最優參數值應用于一個不穩定的控制系統中。仿真結果表明，尋優得到的PID控制器的比例、積分和微分環節的最優值，可以使得控制系統具有很好的穩態性能和動態性能，提高了控制系統的魯棒性。

參考文獻

[1] 王凌.智能優化算法及其應用[M] .北京：清華大學出版社，2001：45-86.

[2] 茍軒，謝華，程玉華，等.模糊PID算法在雙閉環溫控系統中的應用[J] .中國測試，2011，37（4）：75-77，84.

[3] 馮冬青，邢廣成.基于改進PSO算法的多變量PID型神經網絡控制[J] .系統仿真學報，2011，23（2）：363-366.

[4] 田艷兵.基于PSO的自整定PID溫度控制研究[J] .化工自動化及儀表，2010（10）：82-84.

[5] 張麗平，俞歡軍，陳德釗，等.粒子群優化算法的分析與改進[J] .信息與控制，2004，33（5）：513-517.

[6] 史峰，王輝，郭磊，等. Matlab智能算法[M] .北京：北京航空航天大學出版社，2010（12）.

[7] 崔長彩，李兵，張認成.粒子群優化算法[J] .華僑大學學報：自然科學版，2006，27（4）：343-347.

[8] 張敏慧.改進的粒子群計算智能算法及其多目標優化的應用研究[D] .杭州：浙江大學，2005.

[9] 呂振肅，侯志榮.自適應變異的粒子群優化算法[J] .電子學報，2004，32（3）：416-420.

[10] 王啟付，王戰江，王書亭.一種動態改變慣性權重的粒子群優化算法[J] .中國機械工程，2005，16（11）：945-948.

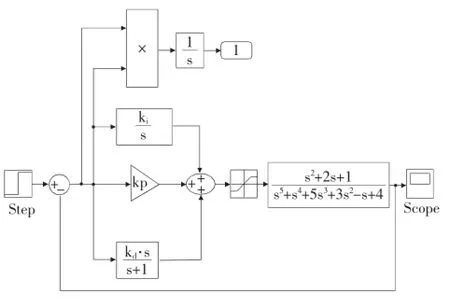
圖2　Simulink環境下PID控制系統的仿真模型

Research on PID controller based on improved PSO algorithm

ZHANG Yan-hong

（School of Electronic Information & Electric Engineering，Changzhou Institute of Technology，Changzhou 213002，China）

Abstract:For the shortcomings of easily falling into local optimum and lower search precision in common particle swarm optimization（PSO）algorithm，an improved PSO algorithm was studied. The inertia weight coefficient ω plays a key role on whether PSO algorithm falling into local optimum or not，so it is linearly reduced by the improved PSO algorithm. The parameters of PID controller are also optimized by the improved PSO algorithm and the optimized parameters are used in the control system. The simulation results show that the improved PSO algorithm does not fall into local optimal and the optimal parameters of the PID controller can be obtained，which makes the performance index of the control system optimal with better robustness.

Key words:PSO；controller；parameter optimization；performance index；robustness

基金項目：常州工學院科研基金項目（YN1216）

收稿日期：2012-10-22；

doi：10.11857/j.issn.1674-5124.2013.05.026

文章編號：1674-5124（2013）05-0096-03

文獻標志碼：A

中圖分類號：TP273；TP214；N945.13；TM930.12

作者簡介：張燕紅（1979-），女，山東德州市人，講師，研究方向為智能控制。