淺談數學問題提出能力的培養

摘 要：問題提出是提高學生問題解決能力的一種手段；問題提出還是促進學生理解數學的一個窗口；問題提出更能改進學生對數學的態度。針對學生提出數學問題能力缺乏的原因，從構成學生問題提出能力的因素入手，在創設的情境中，在自學的過程中，在反思的觀照中，有效培養學生提出數學問題的能力。

關鍵詞：數學；問題提出；培養方法

《義務教育數學課程標準（2011年版）》在“問題解決”的課程目標中指出：初步學會從數學的角度發現問題和提出問題，綜合運用數學知識解決簡單的實際問題，增強應用意識，提高實踐能力。由此可見，“問題提出”與“問題解決”一樣，都是數學活動的重要組成部分。問得多，學的東西就多；問得深，學得也深；不再問了，思維大半停止了，學習大半停頓了。在當今的課堂中，我們只能看到學生踴躍舉手回答問題，而較少聽到學生提出自己不懂的問題。在一次小學數學教學錄像優質課評比中，120節參評課中僅有2節課出現了讓學生提問的環節，所占比率實在太低。就算教師留出時間讓學生提問題，等待多時，得到的結果多半是靜默一片，或是“沒有問題”的高聲齊答。大多數教師也樂得順水推舟，鳴金收場。學生為什么會有疑不問？學生為什么不會提問呢？

一、學生提出問題能力缺乏的原因

原因之一：受應試教育的毒害。現今的教師，明知該在課堂上要讓學生自主探索，但在應試教育的重壓下，還是不得不抓緊時間，多多提問，多多講解，仿佛這樣抓緊了課堂的分分秒秒，心中才感覺踏實。至于學生提問的能力，在現行的考試制度下，我們還難以考查。因此，教師也對提出問題的重要性缺乏足夠重視，自然就放棄了培養。而把目光停留在讓學生解決教師所提供的現成問題上。

原因之二：擔心無法駕馭課堂。學生提出問題的水平必然參差不齊，提問涉及的面必然廣泛，面對這難以預料的復雜情況，教師教學必然不能按照既定方案“順利”進行。為了避免麻煩和尷尬，于是僅安排少量時間讓學生提問，其實是走走過場而已。學生也是明察秋毫，配合默契，漸漸地，對沒有學生提問的課堂，我們就都習慣并認可了。

原因之三：客觀條件的限制。課堂上，有限的教學情境資源幾乎都配備好了相關的問題，教師和教科書幾乎包辦了課堂上所有問題的提出，學生呢，只有乖乖地舉手回答現成的問題。學生提問的權利被剝奪，“思想的源泉”從上游被斬斷，學生自然就提不出有價值的問題了。

所思所感：學生喪失提問的興趣和能力，必然導致學習主動性的缺失，這是學習上比較可怕的現象。由學生提出的問題，可能比較淺顯，但它是學生知識內化的結晶。研究表明，學生對提問的興趣，遠遠大于回答問題的興趣。學生間通過提問，可互相啟發，共同完善，組成一個多樣、開放的問題體系，對學生提問沒涉及的內容，教師可再補充提問。因此，我們不妨在呈現學習材料后，讓學生先動動腦筋，來提提問題，效果自然不言而喻！

二、學生問題提出能力的培養方法

構成學生問題提出能力的因素至少包括：自我對情境的觀察、解釋能力，對數學問題結構的認識和理解能力，對已知問題的再闡述能力等。因此，教師可設計如下一些訓練，以培養學生問題提出的能力。

1.合理拓展——在創設的數學情境中提出問題

數學情境是含有相關數學知識和數學思想方法的情境，同時也是數學知識產生的背景。它不僅能激發數學問題的提出，也能為數學問題的提出和解決提供相應的信息和依據。在數學情境中讓學生通過自我對情境的觀察、解釋，形成自己的數學認識和相應的數學結構，那么，數學問題也就自然地在頭腦中形成。

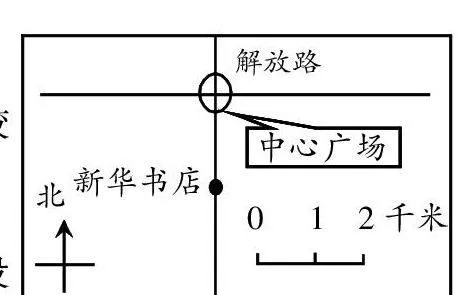
例如在平面圖形的總復習中，為培養學生綜合提取知識的能力，教師出示了圖文結合的如下信息：

右圖是某商業區的平面圖。

要求學生據此情境提出較易和較難的2個問題。

除了部分學生給出的問題明顯沒有難易之分外，學生所提的問題主要有以下類型。

A類：未擴展的問題。如“新華書店在中心廣場南多少千米處？”此類問題對給定情境未作任何擴展。

B類：擴展的問題。如“郵電大樓位于中心廣場東面3千米處，請你用‘？’在圖中表示出郵電大樓的位置。”此類問題借想象對情境進行了合理的擴展，屬較好的問題。

C類：提出的問題“陳述不清或語意含糊”。如：“步行街在東面3千米處，請你畫出這條街。”“文化宮在西邊什么地方？”等。

D類：所提問題完全脫離情境。如：“三角形面積怎樣計算？”“垂線怎么畫？”之類的問題。

令人遺憾的是，沒有教師的提示，學生提不出超越圖上情境的生活問題，如“乘出租車從新華書店——中心廣場——某處（在圖上標示），要付車費多少元？”“小明1分鐘走100米，從新華書店——中心廣場，小明步行約需多少時間？”等問題，這類問題是脫離了機械模仿，在一定的范圍內進行了合理的再創造，從而編制出的一個組合問題。這是產生新問題的一種重要方法。

對學生進行這一訓練的關鍵之處是問題情境的合理設置，而對問題情境的設置可選取現實生活中的一些問題，數學中的原問題，數學史上的一些問題等。在教學中，教師要善于創設形成問題的數學情境，使之與學生已有的數學認知結構相適應，只有這樣，學生才能通過挖掘數學情境中的數學關系，提出更有意義的數學問題，從而使他們提出數學問題與解決數學問題的能力得到進一步發展。

2.比較聯想——在自學的過程中提出問題

學生自學課本的過程也就是吸收、理解和生成問題的過程。學生對所學內容理解得越透徹，所提的問題也就越有深度。不同層次的學生在自學過程中都會產生這樣、那樣的問題，教師所要做的就是在提出問題的方向上、策略上、表述上給予指導，讓學生逐漸掌握方法，提高發現問題、提出問題的能力。

例如，在自學“比例尺”一課后，學生提出了很多問題，大致可以歸為以下幾類：A類，就事論事的問題。如什么叫比例尺？怎樣求一幅圖的比例尺？B類是運用歸納、比較的方法提出的問題。如：求圖上距離或實際距離時需注意什么？比例尺的前項為什么通常要寫成1？比例尺是尺嗎？C類是通過聯想、變式、發散思維等提出的新問題。如：比例尺有什么用處？還有沒有其他的比例尺？不同層次問題的提出，反映了學生不同的認知水平和解題策略，也為如何有針對性地培養不同學生的提問能力提供了依據。當然，這絕不是說教師只對“較好的問題”作出積極的反映，對一般的問題也要作出積極的回應和妥善的處理。

在問題提出的過程中，學生一般都聯系已有的知識或圍繞書本內容提出問題，除此之外，教師還要引導學生聯系生活實際提出問題。實踐證明，聯系現實生活的數學問題的提出，能有效激起學生問題提出的興趣，增強學生問題提出的自信感。

3.質疑追問——在反思的觀照中提出問題

反思是問題解決過程中一個必要的環節。它能有效促進學生問題解決能力的提高。在學習后的反思觀照中通過逆向追問，有利于促進學生對問題整體的理解，有利于學生作出求異、求變的思索，也有利于更好地加深對知識的理解。

如在教學了圓柱的表面積和體積計算后，大部分學生對表面積與體積的計算方法易產生混淆。我校一位教師就讓學生反思學習的過程，提出質疑追問性的問題，來幫助理解表面積與體積不同的計算方法。經歷了順向性的提問和一番等待后，有一個調皮的男生說：“請同學們設計一個實驗性的活動來證明求體積用底面周長×高是錯誤的，可以嗎？”學生明確任務后，紛紛以小組為單位展開討論，提出設想，然后籌集材料，開展驗證性的實驗。精彩的提問引出了精彩的演示，在小組匯報交流時學生各展所長，方法多樣。方法一：用圓柱形罐頭裝滿了水，倒入量杯中測出水的體積，然后再測量出圓柱形罐頭的底面周長和高，求出它們的乘積。這時將計算出的結果與用量杯測出的體積相比，就能發現結果不符。方法二：將兩張一樣大的長方形硬紙板分別圍成一個圓柱體和一個長方體（用長方形的寬作高），這樣圍成的形體，底面周長和高都是相等的。我們把它們平放在木板上，里面裝滿沙（不要壓緊）。通過稱量，學生發現兩個形體所裝的沙的體積是不等的，就可以從反面推斷出底面周長×高不能準確地反映容器體積的大小。方法三：用小正方體擺成底面周長相等、高也相等但形狀不同的長方體。數一數擺成的長方體包含的體積單位，從長方體的體積不能用底面周長×高計算，類似地聯想到，圓柱體的體積也不能用底面周長×高計算……學生再反思其中道理提出問題，發現“底面周長并不表示底面可放多少個體積單位。”在反思后提出質疑性的追問，它既使學生在深思咀嚼中更加活化所學內容的“養料”，增強靈活應用知識的能力，又使他們能更加主動地學習和發展。這樣的提問對一般性的問題作了有效的拓展、創新，提問的水平是相當高的。當然，提出質疑性的問題，不需面面俱到，但要求異、生疑、思變，從而提出有創意的問題。

問題提出是數學活動的顯著特點；問題提出也是提高學生問題解決能力的一種手段；問題提出還是促進學生理解數學的一個窗口；問題提出更能改進學生對數學的態度。創新始于問題的提出，而“數學上的創造能力在一定程度上表現為能提出大量的、相異的問題的能力”。較受關注的“研究性學習”的核心也是學生問題的提出，“對話式教學”，也強調教學通過師生相互提問，平等對話而進行。總的來說，數學問題提出是新的時代擺在我們每位數學教育工作者面前的一項重要的課題，值得我們深入地研究！

參考文獻：

[1]邱學華，張良朋.2011年小學數學教育熱點問題探討[J]. 小學教學，2012（3）.

[2]聶必凱.對數學問題的構成及提出的探討[J].貴州師范大學學報，2001（1）.

[3]汪秉彝，呂傳漢.創新與中小學數學教育[J].數學教育學報，2000（9）.

[4]聶必凱，汪秉彝，呂傳漢.關于數學問題提出的若干思考[J].數學教育學報，2003（5）.

（作者單位 江蘇省常熟市新區小學）