利用遺傳算法優(yōu)化的ARIMA-BP組合模型預測手足口病發(fā)病趨勢

吳文博，李虹艾，萬鵬程，袁秀琴(.南華大學公共衛(wèi)生學院，湖南 衡陽 400；.南華大學經(jīng)濟管理學院)

近年來，手足口病的發(fā)病數(shù)逐年增多，作為丙類傳染病中為我省重點監(jiān)測的疾病之一，因其發(fā)病率高、目前尚無疫苗進行免疫接種、并發(fā)癥危害大，故其防控形勢較為嚴峻。在傳染病的防控中，通過建立相對準確的統(tǒng)計預測模型，從而建立預警監(jiān)測機制，為制定防控政策和衛(wèi)生資源配置提供依據(jù)，這是傳染病防控的重點及難點之一[1]。本文基于某市近年來手足口病的發(fā)病資料，先后建立差分自回歸移動平均模型(ARIMA)、遺傳算法(Gentic Algorithm,GA)優(yōu)化的ARIMA-BP神經(jīng)網(wǎng)絡(luò)模型，比較兩種模型的預測準確性，并探討組合模型在預測方面的優(yōu)越性。

1 材料與方法

1.1 資料來源

數(shù)據(jù)資料來源于中國疾病預防控制信息系統(tǒng)(傳染病報告信息管理系統(tǒng))，按發(fā)病日期檢索某市2009年1月1日～2013年12月31日的手足口病月發(fā)病數(shù)。

1.2 方法

將數(shù)據(jù)導入SPSS18.0中，檢查有無缺失數(shù)據(jù)。以2009年1月1日～2012年12月的發(fā)病數(shù)據(jù)作為模型擬合值，預測2013年手足口病月發(fā)病數(shù)，將預測值與實際值進行比較，以相對偏差的大小衡量模型的精確性。在建模方法上，首先建立ARIMA模型，將ARIMA模型預測值作為BP神經(jīng)網(wǎng)絡(luò)的輸入值，真實值作為輸出值，同時應用遺傳算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)，不斷尋找預測值與真實值的關(guān)系，從而調(diào)整ARIMA模型的預測精度。比較這兩種模型的相對偏差，并對模型預測精度進行評價。

1.3 原理

1.3.1 ARIMA模型 ARIMA模型的基本思想是將預測對象隨時間推移而形成的數(shù)據(jù)序列視為一個隨機序列，用一定的數(shù)學模型來近似描述這個序列[2]。該模型由美國數(shù)學家Box與英國統(tǒng)計學家Jenkins提出，在預測具有季節(jié)周期性的時間序列中，以乘積季節(jié)性模型最為常用，記ARIMA(p,d,q)(P,D,Q)n，其中p,q為非季節(jié)性模型的自回歸項及移動平均項數(shù)，d為時間序列平穩(wěn)化時所做的差分次數(shù)；P,Q為季節(jié)性模型的自回歸及移動平均項，D為季節(jié)差分的階數(shù)。其建模過程見圖1。

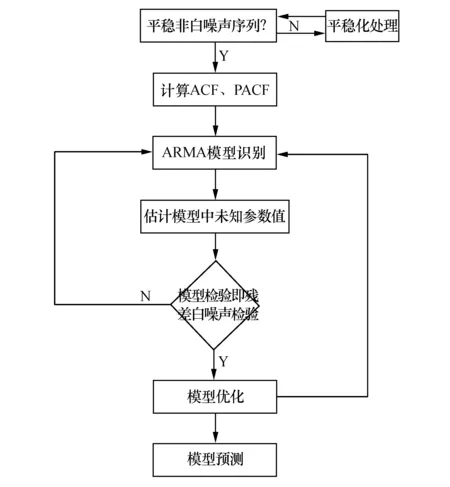
圖1 ARIMA的建模過程

1.3.2 BP神經(jīng)網(wǎng)絡(luò)及遺傳算法 BP神經(jīng)網(wǎng)絡(luò)是一種多層前饋神經(jīng)網(wǎng)絡(luò)，該網(wǎng)絡(luò)的主要特點是信號前向傳遞，誤差反向傳播。在前向傳遞中，輸入信號從輸入層經(jīng)隱含層逐層處理，直至輸出層。每一層的神經(jīng)元狀態(tài)只影響下一層神經(jīng)元狀態(tài)[3]。如果輸出層得不到期望輸出，則轉(zhuǎn)入反向傳播，根據(jù)預測誤差調(diào)整網(wǎng)絡(luò)權(quán)值和閾值，從而使BP神經(jīng)網(wǎng)絡(luò)預測輸出不斷逼近期望輸出。BP神經(jīng)網(wǎng)絡(luò)的拓撲結(jié)構(gòu)如圖2所示。根據(jù)輸入向量X，輸入層和隱含層間連接權(quán)值ωij，以及隱含層閾值a，可以計算隱含層輸出向量H，即：

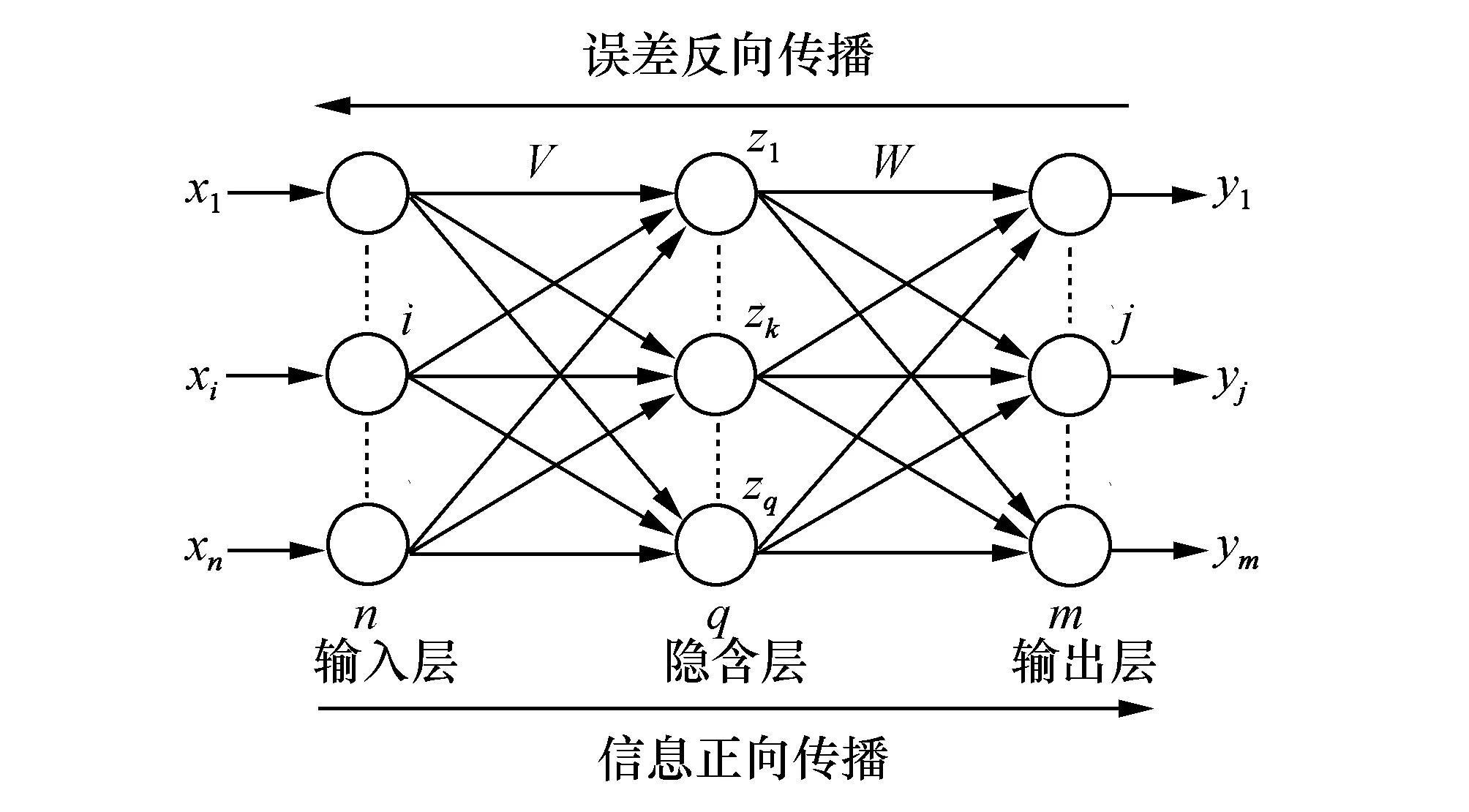
圖2 BP神經(jīng)網(wǎng)絡(luò)拓補結(jié)構(gòu)

但BP神經(jīng)網(wǎng)絡(luò)容易受數(shù)據(jù)極值的影響，從而導致預測精度的下降，同時由于各層權(quán)重的權(quán)值是主觀經(jīng)驗確定的，導致BP神經(jīng)網(wǎng)絡(luò)的主觀傾向性過大，為此引入GA算法。

遺傳算法(Genetic Algorithm，GA)是一種進化算法，其基本原理是仿效生物界中的“物競天擇、適者生存”的演化法則。遺傳算法的做法是把問題參數(shù)編碼為染色體，再利用迭代的方式進行選擇、交叉以及變異等運算來交換種群中染色體的信息，最終生成符合優(yōu)化目標的染色體[4]。遺傳算法所優(yōu)化的內(nèi)容是BP神經(jīng)網(wǎng)絡(luò)的初始權(quán)值和閾值，神經(jīng)網(wǎng)絡(luò)的權(quán)值和閾值一般是通過隨機初始化為[-0.5，0.5]區(qū)間的隨機數(shù)，這個初始化參數(shù)對網(wǎng)絡(luò)訓練的影響很大，引入遺傳算法就是為了優(yōu)化出最佳的初始權(quán)值和閾值,以提高研究的預測精度。

1.4 軟件平臺

ARIMA模型構(gòu)建采用SPSS18.0，神經(jīng)網(wǎng)絡(luò)及遺傳算法編程采用MATLAB 7.0，操作系統(tǒng)為Windows XP。

2 結(jié) 果

2.1 ARIMA模型的建立

(1)模型的平穩(wěn)化識別

首先定義估計區(qū)間，依據(jù)2009年1月～2012年12月的發(fā)病數(shù)擬合模型，并繪制序列圖，見圖3。從序列圖中可見，手足口病發(fā)病數(shù)序列存在著明顯的季節(jié)性周期波動規(guī)律，在每一年5～8月份，出現(xiàn)發(fā)病高峰；報告數(shù)在2012年明顯增多。總的來看，手足口病發(fā)病數(shù)呈現(xiàn)逐年增多的趨勢，提示該序列是一個非平穩(wěn)的序列，需對其進行差分，和對數(shù)轉(zhuǎn)化，以達到序列平穩(wěn)化的目的。

(2)季節(jié)性ARIMA模型的建立：通過做出自相關(guān)函數(shù)(ACF)、偏自相關(guān)函數(shù)(PACF)圖，見圖4。依據(jù)“截尾性”估計季節(jié)性模型參數(shù)；同時在殘差中識別非季節(jié)性模型，確定若干個備選模型后，利用Bayesian信息準則(BIC)最小原則，確定最后的模型，模型ARIMA(1,0,0)(1,1,0)12的BIC最小，為13.002。并對該模型進行診斷、對模型參數(shù)進行估計，相關(guān)統(tǒng)計量見表1，表2。同時利用Ljung-Box方法檢驗殘差白噪聲，得到L-B統(tǒng)計量為16.847，P﹥0.05，可以認為殘差為白噪聲序列。綜上，選用ARIMA(1,0,0)(1,1,0)12模型進行預測。

圖3 手足口病發(fā)病數(shù)序列圖

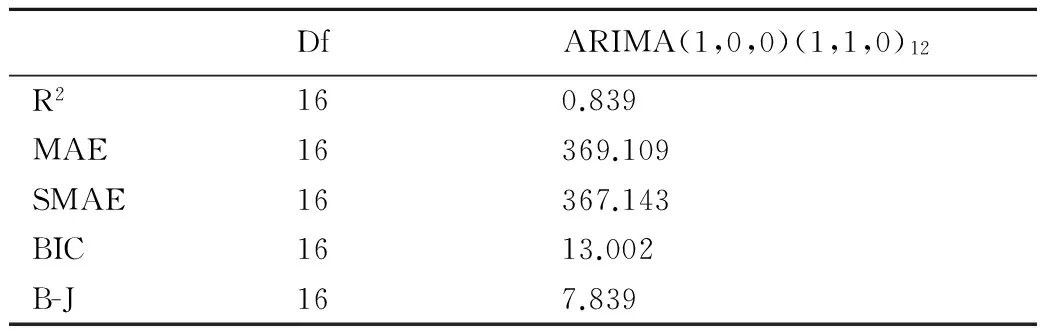
表1 預測模型的相關(guān)檢驗統(tǒng)計量

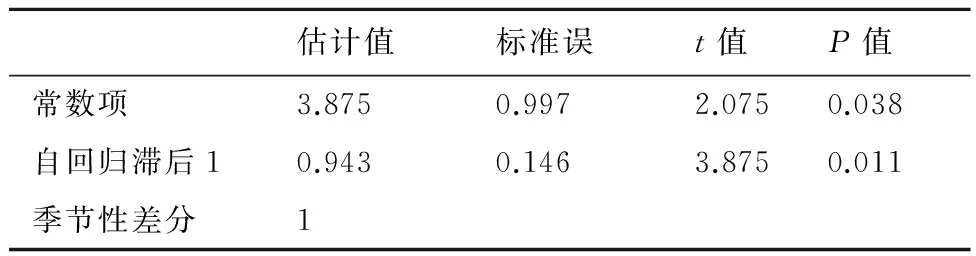
表2 模型的參數(shù)估計

圖4 手足口病序列的ACF、PACF圖

2.2 ARIMA-BP組合模型的建立與遺傳算法的優(yōu)化

(1)將ARIMA模型預測得到的預測值、2013年1月～12月的手足口病實際發(fā)病數(shù)數(shù)據(jù)進行歸一化處理，使其集中在[-0.5,0.5]之間；

(2)學習樣本的選擇

輸出變量：2013年1月～12月的實際觀測值yi。

(3)網(wǎng)絡(luò)初始化，利用遺傳算法進化50代尋找最佳初始權(quán)值和閾值。確定遺傳算法參數(shù)的程序代碼如下：

%%定義遺傳算法參數(shù)

NIND=5; %個體數(shù)目

MAXGEN=50; %最大遺傳代數(shù)

PRECI=10; %變量的二進制位數(shù)

GGAP=0.95; %代溝

px=0.7; %交叉概率

pm=0.01; %變異概率

trace=zeros(N+1,MAXGEN); %尋優(yōu)結(jié)果的初始值

FieldD=[repmat(PRECI,1,N);repmat([-0.5;0.5],1,N);repmat([1;0;1;1],1,N)]; %區(qū)域描述器

(4)依據(jù)遺傳算法尋找的最佳閾值與連接權(quán)值，計算隱含層與輸出層；

(5)計算誤差，不斷迭代更新閾值與權(quán)值，直至誤差保持在穩(wěn)定水平時輸出最后結(jié)果。迭代進化過程中誤差變化見圖5。

圖5 遺傳算法進化過程中誤差的變化

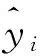
利用BP神經(jīng)網(wǎng)絡(luò)進行預測的程序如下：

net.iw{1,1}=reshape(w1,hiddennum,inputnum);

net.lw{2,1}=reshape(w2,outputnum,hiddennum);

net.b{1}=reshape(B1,hiddennum,1);

net.b{2}=reshape(B2,outputnum,1);

%%訓練網(wǎng)絡(luò)

net=train(net,inputn,outputn);

%BP網(wǎng)絡(luò)預測

%預測數(shù)據(jù)歸一化

inputn_test=P_test./80;

%網(wǎng)絡(luò)預測輸出

an=sim(net,inputn_test);

2.3 ARIMA模型與組合模型的預測精度比較

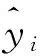
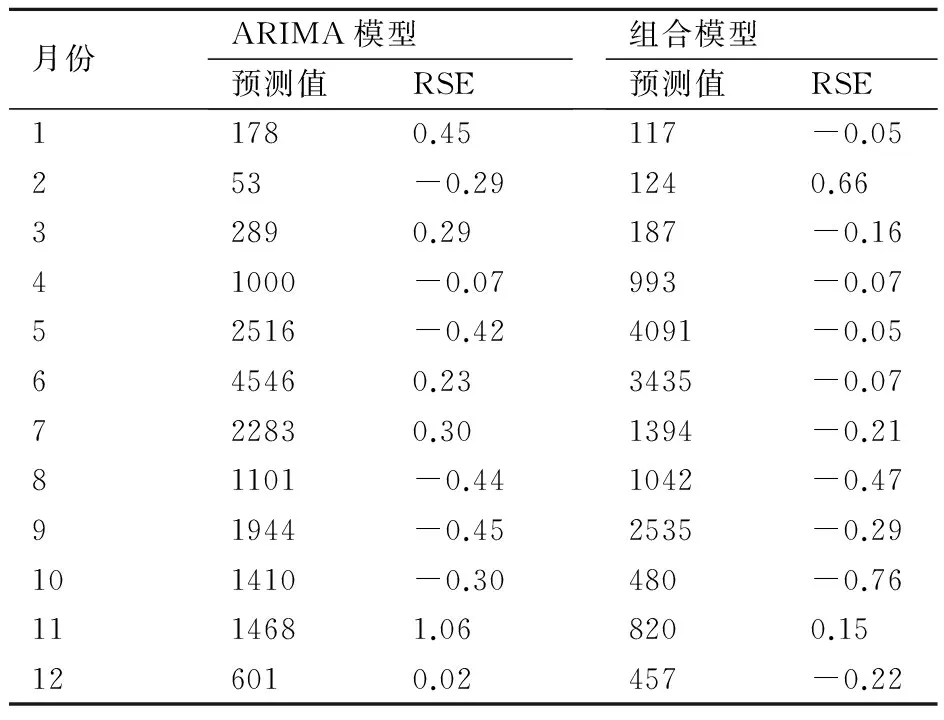
表3 ARIMA模型與組合模型預測2013年各月份發(fā)病數(shù)的結(jié)果比較

由表4可見，組合模型的平均預測精度高于ARIMA模型，且對于部分極端值(尤其是發(fā)病高峰5～8月)的預測較為準確。對模型整體的評價指標見表4。其中決定系數(shù)R2用來反映模型的擬合效果，即：

SSi表示預測值的離均差平方和，SSo表示實際值得離均差平方和。

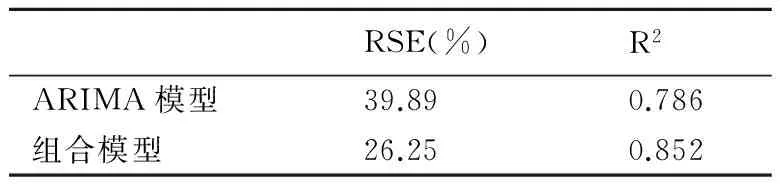
表4 兩種模型的綜合評價

3 討 論

傳染病的發(fā)病預測是當前傳染病疾病預防與控制的難點[5]。用于發(fā)病預測的方法有很多，實際工作中通常的做法是定性預測法，即基于日常的疾病監(jiān)測數(shù)據(jù)、傳染病的發(fā)病特點，進行趨勢外推。這種做法主觀因素較大，沒有充分利用監(jiān)測數(shù)據(jù)，難以保證預測的準確性。對于組合模型，國內(nèi)外相關(guān)的研究相對較少，如：Gamer分解定律、對不同模型給予一定的權(quán)重[6]，但權(quán)重的設(shè)定僅能依靠經(jīng)驗的判斷，導致預測的主觀性增加，影響了預測的精度。有關(guān)基于ARIMA的組合模型預測，朱玉等[7]利用ARIMA-GRNN對猩紅熱的發(fā)病進行擬合；章勤等[8]則利用BP神經(jīng)網(wǎng)絡(luò)對矽肺的發(fā)病情況，進行了預測，取得了較好的效果。雖然上述采用神經(jīng)網(wǎng)絡(luò)的組合預測方法，避免了對各分模型權(quán)重大小選取的討論，但是神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)的閾值以及連接權(quán)值，均需要依靠經(jīng)驗反復設(shè)定，在實際利用中較為繁瑣。本次研究的創(chuàng)新點在于使用了遺傳算法，通過進化代數(shù)的迭代，優(yōu)化了神經(jīng)網(wǎng)絡(luò)參數(shù)，使得預測結(jié)果更加科學可信。

從預測結(jié)果上看，利用遺傳算法優(yōu)化的ARIMA-BP組合模型實現(xiàn)了對手足口病的發(fā)病趨勢的預測，相比于ARIMA模型，該組合模型對極端值的預測效果較好，此外，從整體上看，手足口病的發(fā)病數(shù)年年攀升，需引起足夠重視，由于手足口病致病病原體種類繁多，難以進行免疫接種干預，故應在每年的疾病高發(fā)時期，建立統(tǒng)計預警，加大對托幼機構(gòu)、學校的消毒、衛(wèi)生檢查以及衛(wèi)生宣教；廣大醫(yī)療機構(gòu)應加強監(jiān)測篩檢機制，動員醫(yī)療資源做到早發(fā)現(xiàn)、早診斷、早治療。

由于納入本次建模的數(shù)據(jù)樣本量并不大，組合模型的效果變化并不是非常明顯，但當數(shù)據(jù)量增大時，采用本法的組合模型，將會依舊保持良好的預測精度。此外，介于本模型的非線性映射能力較強、不受極端數(shù)值的影響[9]，基于ARIMA的組合模型尚可以用于金融、人口、水文以及環(huán)境保護領(lǐng)域，但仍需進一步的研究與討論。

[1]羅靜，楊舒，張強，等.時間序列ARIMA在艾滋病疫情預測中的應用[J].重慶醫(yī)學，2012,41(13)：1255-1257.

[2]張晉昕，醫(yī)學時間序列分析及其預測應用相關(guān)問題的研究[D].西安：第四軍醫(yī)大學博士研究生畢業(yè)論文，2000：23-25.

[3]SimonHaykin.神經(jīng)網(wǎng)絡(luò)原理[M].北京：機械工程出版社，2004:154-167.

[4]史峰，王小川，郁磊，等.MATLAB神經(jīng)網(wǎng)絡(luò)30個案例分析[M].北京：北京航天航空大學出版社，2010：21-25.

[5]牟瑾,謝旭,李媛，等.將ARIMA模型應用于深圳市1980～2007重點法定傳染病預測分析[J].預防醫(yī)學論壇，2009，15(11)：1051-1055.

[6]Erxu Pi,Mantri,Sai Ming Ngai.BP-ANN for fitting the temperature-germination model and its application in predicting sowing time and region for bermudagrass[J].PLoS One 2013,11(8)：e82413.

[7]朱玉，夏結(jié)來，王靜.單純ARIMA模型和GRNN-ARIMA組合模型在猩紅熱發(fā)病率中的研究[J].中華流行病學雜志,2009,30(9)：964-966.

[8]章勤，田晶，孫傲冰，等.基于BP神經(jīng)網(wǎng)絡(luò)的矽肺病組合模型預測研究[J].計算機科學，2009,36(4)：265-269.

[9]嚴薇榮，徐勇，楊小兵，等.基于ARIMA-GRNN組合模型的傳染病發(fā)病率預測[J].中國衛(wèi)生統(tǒng)計，2008，25(1)：82-83.