思維圖形化方法的應用＊——談高三復習課中“幾何光學”的教學設計

馬國偉

（常州市第二中學，江蘇 常州 213003）

1 教材分析及教學策略

幾何光學是以光的直線傳播為基礎，采用幾何方法研究光在透明介質中的傳播問題.本課知識點主要包含光的反射，折射和全反射現象，知識難度不大.但近幾年高考中幾何光學出現頻率很高，是高考的一大熱點.在復習中我們采用以思維圖形化方法為主線，知識為載體的方式突破相關問題的重點和難點.

2 教學目標

（1）知識與技能.

① 理解折射定律和折射率的概念；

② 理解并掌握光的全反射現象和發生全反射的條件.

（2）過程與方法.

掌握思維圖形化方法在解決幾何光學問題中的應用.

（3）情感態度、價值觀.

① 理解思維圖形化對解決物理問題的重要性；

② 感受在學習工作中應用思維圖形化帶來的便利.

3 教學重點與難點

（1）教學重點：思維圖形化的應用.

（2）教學難點：全反射的臨界問題分析.

4 課前準備

筆記本電腦（連接網絡，打開QQ），投影儀，手機（打開QQ）.

5 新課引入

在解決物理問題時，為了防止問題過于抽象導致問題的無法解決，我們往往采用將物理問題通過圖形的方式分析以降低問題的難度，達到解決問題的目的.這種方法我們可以稱為思維圖形化.

今天我們復習新的內容——幾何光學，就需要思維圖形化的方法.下面請幾位同學將學案中的基礎梳理填空答案核對一下.（學生回答填空答案，在學生有錯誤時老師予以更正）

6 進入新課

____師：（投影）下面請看投影，這2幅圖是光線由空氣進入玻璃和由玻璃進入空氣的反射和折射如圖1所示.觀察2幅圖發現在圖中除了有入射光線，反射光線，折射光線外還有什么呢？

圖1

生：還有分界面和法線，入射角，反射角和折射角.

師：法線具有什么特點？

生：法線與分界面垂直.

師：經過研究發現，光的反射，折射全反射有以下規律.（教師投影）

（1）反射角等于入射角i＝β；

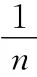
師：我們如何利用這些知識解決幾何光學問題呢？請看例1.（學生思考題目，教師觀察學生做題情況，將學生出現的典型解題錯誤用手機QQ拍照發送到筆記本電腦QQ上）

（1）兩條光線射出玻璃后的交點與O點的距離；

（2）光線Ⅱ從A點入射到與光線I相交所用的時間.

（教師投影展示學生錯誤分析的圖片）

分析學生情況，學生幾乎沒有作圖，問題根本無法解決.如圖3、4，學生作圖，但所作圖形是錯誤的，問題還是不能解決.

圖2

圖3

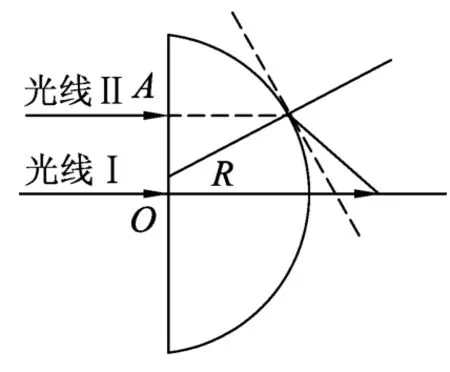
圖4

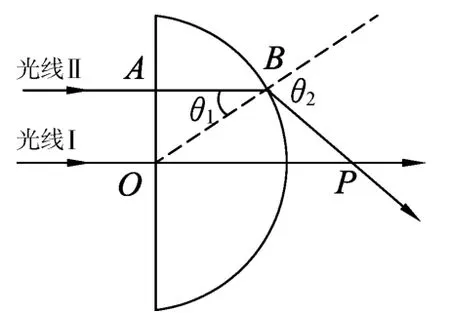
圖5

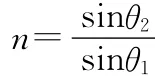
（教師總結并投影）要解決幾何光學問題我們需要3步：（1）根據題意作出光路圖；（2）利用光路圖尋找幾何關系；（3）根據對問題的分析寫表達式并根據必要的推理寫表達式求解.

師：根據由例1總結的思維圖形化解決幾何光學的步驟，請同學們求解例2.（學生思考并解決問題，教師觀察學生做題情況，將學生出現的典型解題錯誤用手機QQ拍照發送到筆記本電腦QQ上）

例2.（2013年江蘇省高考卷）圖6為單反照相機取景器的示意圖，ABCDE為五棱鏡的一個截面，AB⊥BC.光線垂直AB射入，分別在CD和EA上發生反射，且兩次反射的入射角相等，最后光線垂直BC射出.若兩次反射都為全反射，則該五棱鏡折射率的最小值是多少？（計算結果可用三角函數表示）

（教師投影展示學生錯誤分析圖片）

圖7錯誤審題不清，沒有注意題目兩次反射.圖8的錯誤也是審題不清，沒有關注到全反射.而圖9的錯誤為沒有關注出射光線垂直于BC，導致作圖錯誤.

圖6

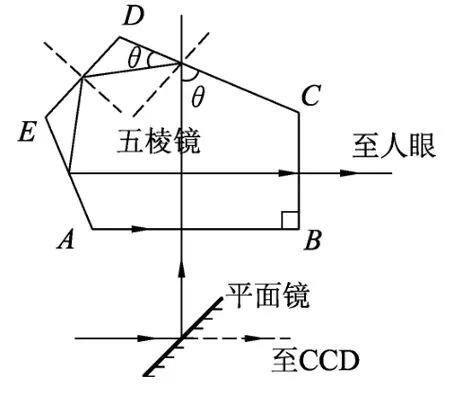
圖7

圖8

圖9

圖10

師：前面2個問題都是只有1條入射光線，我們直接作出光路圖即可，那么如果出現一組光線會怎樣呢？請看例3.（學生思考并解決問題，教師觀察學生的做題情況，將學生的典型錯誤用手機QQ拍照發送到筆記本電腦QQ上）

例3.（2010年重慶高考卷）如圖11所示，空氣中有一折射率為的玻璃柱體，其橫截面是圓心角為90°，半徑為R的扇形OAB.一束平行光平行于橫截面，以45°入射角照射到OA上，OB不透光.若只考慮首次入射到圓弧AB上的光，則圓弧AB上有光透出部分的弧長為

圖11

（教師投影展示學生錯誤分析圖片）如圖12，學生很容易得到過O點的光線折射情況，但會錯誤認為所有光線都從圓弧出射.

教師給予正確分析：如圖13，從中可以發現，隨著入射光線向左平移，在圓弧AB上光線的入射角逐漸增大，當入射角增大到45°時，發生全反射，假設此時為Q點.則有∠AOQ＝15°，又因∠BOP＝30°，可見出射光線部分為圓弧PQ.所以選（B）選項.

圖12

圖13

教師總結：如果問題出現有一組光線，我們可以通過尋找共同情況和變化情況，使思維圖形化完善而予以解決.

師：如果根本就沒有給任何入射光線的問題該怎么辦呢？請看例4.

圖14

問題分析：本題在利用思維圖形化時需要突破2個問題：（1）轉換觀察視角；（2）尋找光線臨界點.而要得到結果還要突破第3個問題：參照實際情況估算.需要教師引導學生一步一步突破.

第1步突破——轉換觀察視角.

師：我們所看到的照片是怎么拍攝出來的呢？

生：光線進入照相機鏡頭在底片上成像.

師：那么這些光線與照片在一個平面內嗎？

生：不在.

師：為了能夠分析光路圖，我們該怎么辦呢？

生：轉換觀察視角.

第2步突破——尋找臨界點.

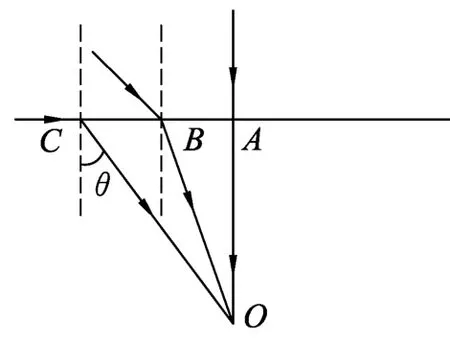
圖15

如圖15，O點為照相機所在位置，直線ABC為水面，過O點正上方的A點的光線可以垂直入射進入照相機.過與A點相距不遠的B點的光線也有一條折射后進入O點.那么是不是所有位置都可以有光線折射后到達O點呢？不是.當折射角θ等于臨界角時，入射角為90°，再向外的所有點的光線都不能經折射到達O點.

第3步突破——參照實際情況估算.

運動員手到腳的實際長度大約為2.1m，按照比例關系，可求得實際半徑.

教師總結：在利用思維圖形化解題時，為了能夠做出思維圖形，有時需要轉換觀察視角，尋求臨界條件.

總之，思維圖形化是高中物理在解決問題時分析問題的一種常用方法.除在幾何光學中做出光路圖外，在力學問題中有受力分析圖，運動問題中有運動簡圖和速度－時間圖像，電路問題中有等效電路圖，電磁場問題中為形象描述引入了電場線和磁感線，這些都是思維圖形化方法的應用.這種方法可以有效地降低問題的思維難度，有利于問題的解決，但作圖時務必要規范、準確、全面.

1 楊萬林.暴露思維過程 重視圖形演變 培養創新意識［J］.科學大眾·教師版，2012（3）.

2 孫路弘.讓圖形展示思維的精彩［J］.銷售與市場·營銷版，2007（2）.

3 劉霽華.以方法為主線的物理教學［J］.物理教學，2008（8）.