內置式永磁同步電動機電感參數計算分析

石有計

(鐵嶺師范高等專科學校，鐵嶺112000)

0 引 言

內置式永磁同步電動機(以下簡稱IPMSM)具有高過載能力、高功率密度、突出的轉矩控制能力、易于弱磁調速而且調速范圍寬等優點。因此，在航空航天、新能源混合電動汽車驅動、風力發電、數控加工等領域得到了廣泛的應用。

IPMSM的電抗參數是電機設計中的重要參數之一，IPMSM的各種性能指標和力能指標與電機電感參數密切相關。磁路飽和對IPMSM的電感參數會產生很大影響［1－3］，對相關問題很多文獻做了大量研究，而研究磁路間交叉耦合作用對電感特性產生的影響方面的文獻不多。由于IPMSM具有復雜的轉子磁路結構，磁路飽和現象相當嚴重，并且交、直軸磁場存在交叉耦合作用，使得電感參數難以精確計算，而電感參數對永磁電機的運行特性會產生重要影響。另一方面，隨著運行點的變化，實際電機中磁路的飽和程度和磁場分布也會相應發生改變，這會引起電感參數發生改變。而電感參數的不確定性會進一步波及對電機運行特性分析的準確性。鑒于此，本文對永磁同步電動機的電感參數在不同工況下的準確計算方法進行研究。

1 IPMSM 的 d－q 軸數學模型［4－5］

d－q坐標系下磁鏈傳統方程:

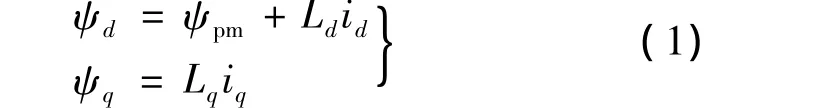
式中:id為d軸等效電流，iq為q軸等效電流;Ld為d軸等效電感，Lq為q軸等效電感;ψd和ψq分別為d軸和q軸等效磁鏈，ψpm為永磁體產生的磁鏈。d－q坐標系下電壓方程:

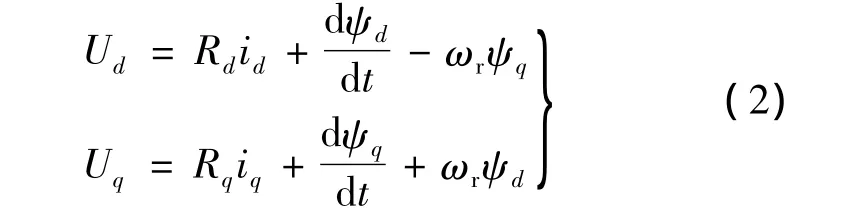
式中:Ud和Uq分別為d軸和q軸等效電壓;ωr為轉子旋轉電角速度。

2 電感參數計算模型

2.1 不考慮電機磁路飽和

假設d－q軸完全解耦的情況下，電感計算模型如下:［6］

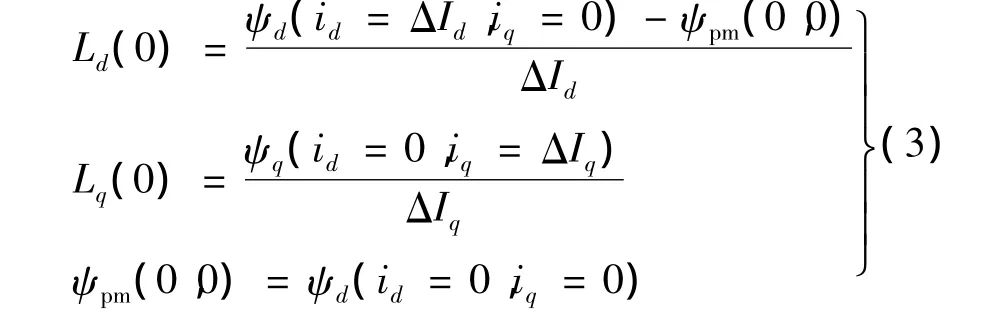
式(3)中的ΔId和ΔIq一般取額定電流的 5%～10%進行計算。

2.2 考慮電機磁路飽和

假設d－q軸完全解耦情況下，電感計算模型:

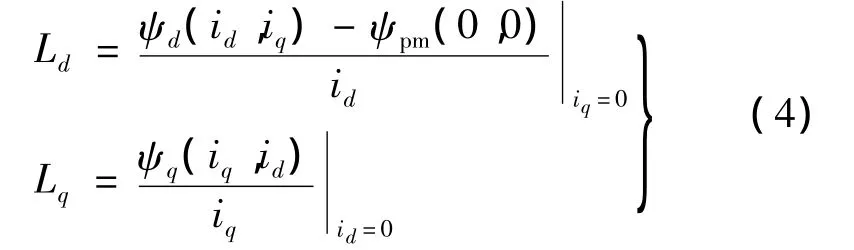
實際上，隨著轉子鐵心的飽和度的變化磁鏈會發生變化，則計算得到的電感參數也會隨磁路的飽和而發生變化。

2.3 考慮交叉飽和的電感計算模型

永磁電機d，q軸磁路存在共同部分，使得d，q軸間存在交叉耦合作用［7－8］。考慮交叉耦合的磁鏈表達式如下:

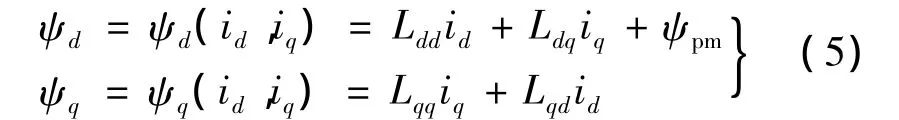
式中:Ldd為d軸自感;Lqq為q軸自感;Ldq和Lqd分別是d和q軸間交叉耦合電感。進一步得到如下電感參數計算模型［9］:

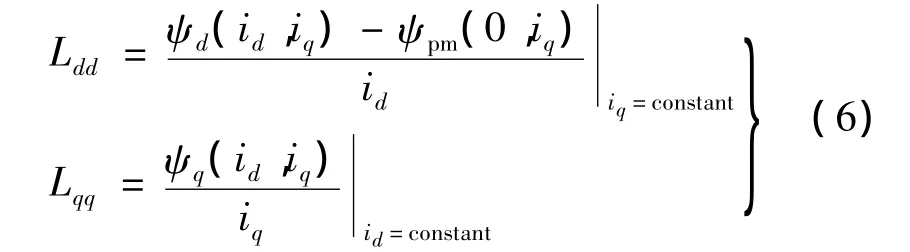
2.4 考慮交叉耦合的修正的電感計算模型

IPMSM的磁場是由永磁體、電樞電流id和iq的共同激勵產生的，在d軸去磁電流變化時，電機磁路的飽和程度也會相應的改變。在以下兩種情況時，一種是永磁體單獨作用，另一種是電流和永磁體共同作用，式(6)Ldd表達式中，電機的飽和程度在兩種狀況下難以確保相同，因此不能準確地計及交叉飽和對電感參數的影響。若要求得準確的d軸電感，必須使得磁路的磁導率μ在兩種情況下不變，這樣電機就具有相同的飽和程度。準確計算方法:假設在永磁體和電流共同作用時的磁導率為μ，在保持磁導率不發生變化的情形下，然后去掉永磁體，再加上相同的電流來計算d軸電感值，如下:

3 電感參數的有限元計算與分析

3.1 內置式永磁同步電機有限元建模及主要參數

用Ansoft有限元分析軟件創建IPMSM二維有限元瞬態模型如圖1所示，其基本設計參數如表1所示。

圖1 IPMSM有限元模型

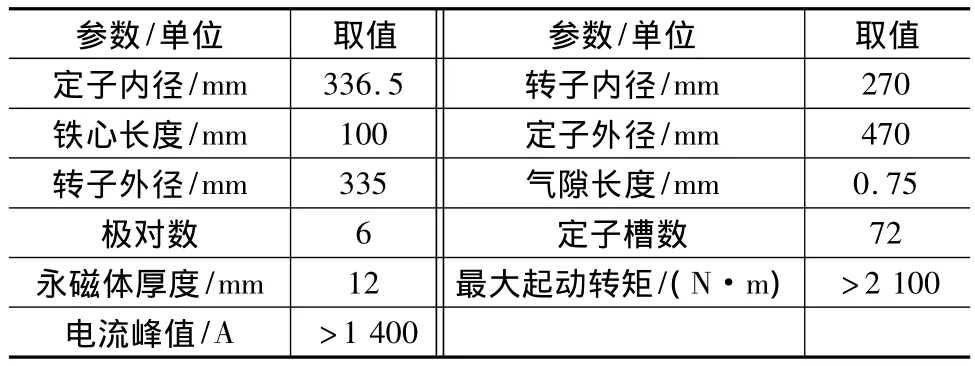
表1 IPMSM設計參數

3.2 計算方法

基于有限元方法，利用 Ansoft軟件進行電磁場分析的結果來計算各個電感參數的方法如下［10］:在某一運行點下，求取永磁體磁鏈ψpm，id，iq共同作用時該運行點的磁導率μ，保持該點磁導率μ不變，然后分別求取id單獨作用產生的ψd和ψqd;iq單獨作用產生的ψq和ψdq;永磁體單獨作用產生的磁鏈。再通過Ansoft軟件處理后得到此時對應的電感參數;對不同運行點進行計算，得到對應于不同運行點的電感參數。該法同時考慮了磁路飽和以及d，q軸磁路交叉耦合對d，q軸電感參數的影響。

電感參數的計算式:

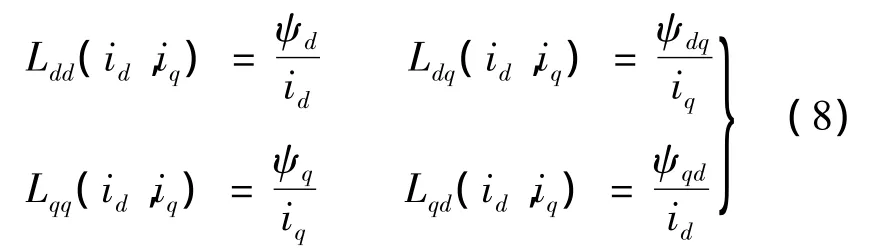
3.3 計算結果與分析

根據所建樣機模型，向電機通入不同的定子電流，其范圍:id∈(－850，0)A，iq∈(850，0)A。計算得到不同電流下的d軸總磁鏈ψd和q軸總磁鏈ψq。

對應某一個q軸電流時，ψd隨id的變化如圖2(a)所示，對應某一個d軸弱磁電流時，ψq隨iq的變化如圖2(b)所示。

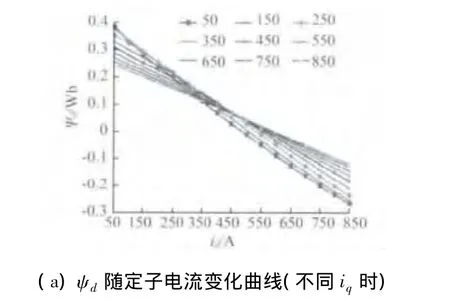
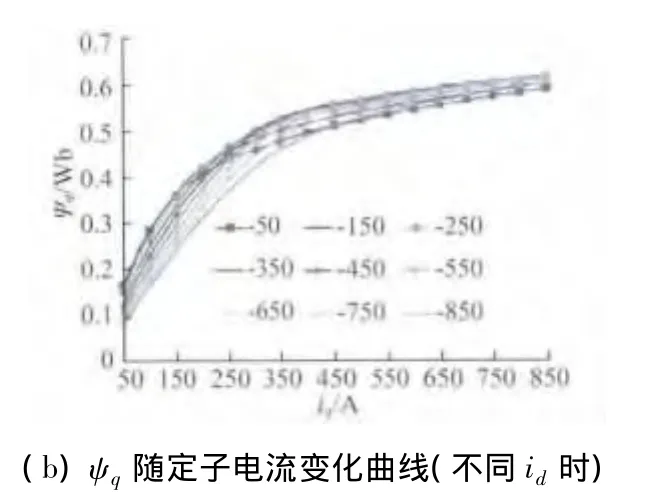
圖2 d軸和q軸磁鏈隨定子電流變化圖

由圖2可以看出，ψd隨iq的不同相對變化較大，而ψq隨id的不同并沒有顯著變化。

在得到d，q軸總磁鏈情況下，保存運行點磁導率不變，從總的磁鏈中分解出id和iq單獨作用產生的磁鏈，根據式(8)計算得出d，q軸各電感參數隨d，q軸電流變化的曲線，如圖3和圖4所示。

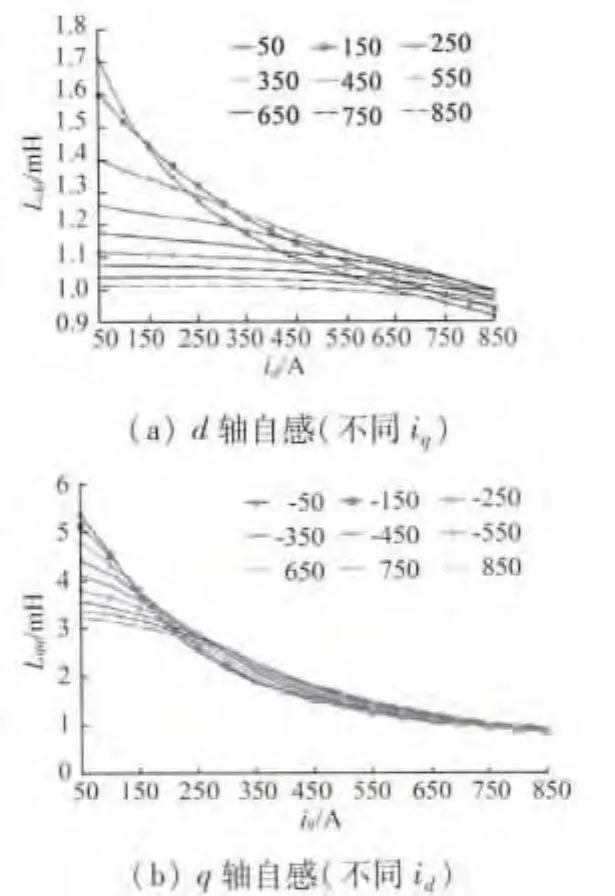
圖3 d，q軸自感參數

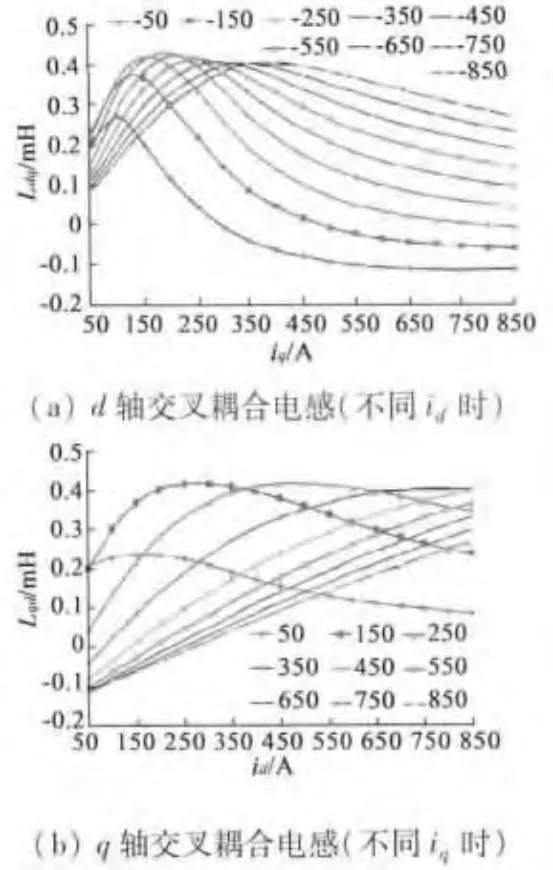
圖4 d，q軸交叉耦合電感參數

圖3(a)給出了對應不同iq時，d軸自感參數Ldd隨弱磁電流id變化的情況;圖3(b)給出了不同id時，q軸自感參數Lqq隨iq變化的情況。當iq較小(iq＜250 A)時，隨著id的逐漸減小，由圖3(a)可以看出，Ldd會逐漸增大;由圖3(b)可以看出，Lqq也逐漸增大。而當iq增加到一定數值時，id的變化對Ldd和Lqq的影響幾乎可以忽略不計，Ldd可看成是常數。而iq增大使Lqq下降較多。由圖3整體上看，iq較小時，Ldd約為 Lqq的1/4 ～1/3，iq較大時，Lqq近似等于Ldd的值。Ldd和Lqq隨電流的變化不相同的原因是因為d軸磁路不易飽和而q軸磁路飽和。

圖4(a)給出了不同d軸弱磁電流時，Ldq隨iq變化的情況。由圖4(a)可看出，iq發生變化時，對Ldq的影響不大，且當去磁電流id較大時，Ldq值較大。圖4(b)給出了不同q軸電流時，q軸交叉耦合自感參數Lqd隨id變化的情況。由圖4(b)可看出，id的變化對Lqd影響較大，當iq數值較大時，隨著去磁id減小，Lqd呈線性減小。總之id和iq對交叉耦合電感都會產生影響，但id影響要大于iq。由圖還可以看出，在磁路沒有達到飽和狀態時，交叉耦合電感數值比較大些，能達到約d軸自感的30%。通過計算表明兩種交叉耦合電感值相等:Ldq=Lqd。原因是兩種交叉耦合磁鏈所通過的路徑是共磁路區域，磁路飽和度是相同的。而同一飽和度的磁路下，單位電流產生的磁鏈相同，所以電感相同。

4 實驗驗證

隨著電機磁路飽和程度的變化，電抗參數也隨之改變，要準確測量其數值不太容易。本文采用一種間接驗證的方法，即應用以下兩種參數對電機空載和負載特性分別進行仿真，一種是通過上述計算得到的電感參數(變參數);另一種是不考慮飽和因數時的固定參數(恒參數)，然后與實測結果進行對比。

4.1 空載特性仿真與實測對比

兩種不同方法的仿真結果與樣機實測的空載特性如圖5所示。

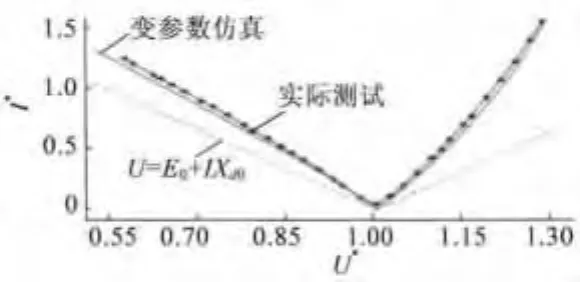
圖5 空載特性仿真與實測對比

從圖5中可以看出，變參數仿真和實際測試結果吻合度很好，而使用恒參數的仿真結果與實測數據差異較大。

4.2 負載特性仿真與實測對比

兩種不同方法的功角特性曲線仿真結果與實測對比如圖6所示。

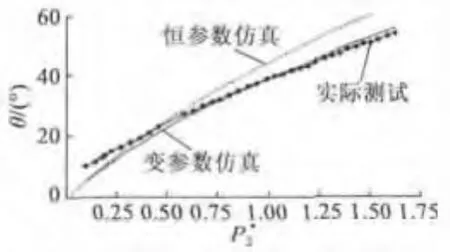
圖6 負載特性仿真與實測對比

從圖6可看出，相同負載率下，在負載較大時，和恒參數仿真比較，變參數仿真結果非常接近實測值。

5 結 語

本文利用Ansoft二維靜態有限元對IPMSM進行電磁場分析的結果顯示:在不同運行點，隨著磁路飽和程度的變化，永磁體、交直軸電流產生磁鏈也會隨之改變。在不同運行點考慮磁路飽和及交叉耦合，運用保存相對磁導率不變的方法，分析計算了d，q軸自感參數和d，q軸交叉耦合電感參數。結果表明:d軸自感參數隨電流變化很小，q軸自感參數由于受到飽和的影響而顯著下降，而且交叉耦合電感Ldq和Lqd既受d軸電流id影響，又受q軸電流iq的影響，但id影響要大于iq。并且 Ldq和Lqd值基本相等，在磁路處于不飽和狀態時數值相對大些，大約是d軸自感參數的30% ，并隨飽和程度逐漸增加而逐漸減小。利用計算得到的電感及永磁磁鏈參數，通過對樣機的空載和負載特性仿真，并與實際測試結果比較，驗證了參數計算方法的合理性。

［1］李景燦，廖勇，姚俊.飽和對埋入式永磁同步電機電感特性的影響［J］.重慶大學學報，2009，32(11):1285－1290.

［2］付強，王艾萌，魏亮.磁路交叉飽和對內置式永磁同步電機寬調速控制性能影響的研究［J］.微電機，2011，44(1):40－45.

［3］LEE Ji－Young，LEE Sang－Ho，LEE Geun－Ho，et al.Determination of parameters considering magnetic nonlinearity in an interior permanent magnet synchronous motor［J］.IEEE Trans.on Magnetic，2006，42(4):1303－1306.

［4］PANDA S K，XU Jianxin，QIAN Weizhe.Review of torque ripple minimization in PM synchronous motor drives［C］//2008 IEEE Power and Energy Society General Meeting－Conversion and Delivery of Electrical Energy in the 21st Century.IEEE，2008:1－6.

［5］PETROVIC V，ORTEGA R，STANKOVIC A M，et al.Design and implementation of an adaptive controller for torque ripple minimization in PM synchronous motors［J］.IEEE Trans.on Power Electronics，2000，15(5):871－880.

［6］CHEDOT L，FRIEDRICH G.A cross saturation model for interior permanent magnet synchronous machine.Application to a startergenerator［C］//Proc.of the 39th IEEE IAS Annual Meeting.IEEE，2004.

［7］MORIMOTO S，SANADA M，TAKEDA Y.Wide－speed operation of interior permanent magnet synchronous motors with high－performance current regulator［J］.IEEE Trans.on Ind.Appl.，1994，30(4):920－926.

［8］EL－RERAFI A M，WU J.Determination of the parameters representing thecross－magnetizing effect in saturated synchronous machines［J］.IEEE Trans.Energy Conv.，1993，8(3):333－342.

［9］QI G，CHEN J T，ZHU Z Q.Influence of skew and cross－coupling on flux－weakening performance of permanent－magnet brushless AC machines［J］.IEEE Transactions on Magnetics，2009，45(5):2110－2117.

［10］WALKER J A，DAVID G D.Flux－linkage calculation in permanent－magnet motors using the frozen permeabilities method［J］.IEEE Trans.on Magnetic，2005，1(10):3946－3948.