基于新型算法的永磁電機齒槽轉矩削弱方法

李曉寧，吳蘇敏，屠新雅，孔德坤

(1.電子科技大學，成都611731;2.南車株洲電機有限公司，株洲412001)

0 引 言

在永磁電機的工作過程中，如果將定子繞組斷路，電樞齒便會與永磁體相互作用，產生磁阻轉矩，此轉矩即為齒槽轉矩。齒槽轉矩是電機工作過程中產生振動和噪聲的主要原因，輕載及低速運行時更為明顯，在高性能永磁同步電機的設計過程中，應盡量削弱它。以往的研究分析了電機極弧系數是影響齒槽轉矩的重要因素［1］，同時證明了磁體偏心距對齒槽轉矩的影響，認為隨著偏心距增加，齒槽轉矩幅值減小［2］。文獻［3］研究了磁鋼徑向尺寸與齒槽轉矩的關系，此外，定轉子斜槽與氣隙長度也與齒槽轉矩有著密不可分的聯系［4－5］。抑制電機齒槽轉矩有磁極偏移、改變極弧系數、改變磁極磁化方向、磁極偏心、磁極削角、斜槽等［6］，由于斜槽方案在初步設計中已經采用，故本文主要研究永磁電機永磁體厚度、極弧系數、偏心距和氣隙長度與齒槽轉矩之間的關系。

電機結構參數影響其性能，但影響的高度非線性使得求取其準確目標函數及約束條件的難度變得很大。同時在電機的優化過程中，電磁場有限元數值計算方法求解過程需要大量迭代計算，因此需要結合一定的優化算法來減小資源消耗和優化時間。本文利用支持向量機算法建立電機參數與性能的數學模型，然后利用粒子群算法對其進行尋優，得到4個參數的最佳取值使得電機得到最小的齒槽轉矩。

1 電機仿真模型

RMxprt是Ansoft自帶的等效磁路法模塊，可向2D有限元計算模塊中直接導入計算結果并自動生成相應的有限元模型，本文采用Ansoft來完成電機的計算與分析過程。

電機4極36槽，部分參數如表1所示，繞組采用雙層Y形接法，長度設為12 cm。為削弱定子繞組諧波，選用短距繞組，第一節距y1=7。同時為減小氣隙磁場波動，采用定子斜槽設計。

表1 電機原始參數

生成的電機模型如圖1所示。

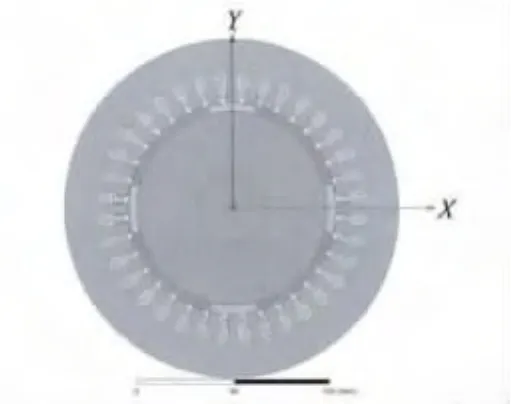
圖1 永磁同步電機模型

齒槽轉矩是定子繞組斷路時產生的，因此需要在建立好的模型中將電源激勵設為0。由于磁場儲能此時集中在氣隙部分，故需要對氣隙部分進行網格加密。電機轉速設為1(°)/s，圖2為生成的齒槽轉矩。

由圖2中可看出，齒槽轉矩與其解析表達式一致，可近似看作正弦波，但此時齒槽轉矩較大，約為3.06 N·m，應通過優化算法加以優化。

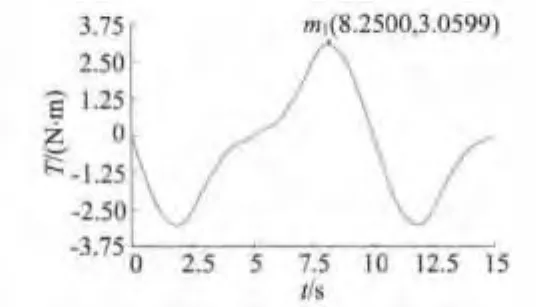
圖2 齒槽轉矩曲線

2 參數優化過程

2.1 支持向量機回歸

支持向量機(SVM)是一種針對有限樣本的模式識別問題進行研究的新型機器學習方法，主要分為兩大類:樣本分類和回歸建模分析。為降低高維問題維數及解決非線性問題，SVM引入了核函數，減小了計算復雜程度受問題維度的影響，而變得只與支持向量的個數相關。統計理論中常用的核函數主要有線性核函數、多項式核函數、高斯徑向基核函數、指數徑向基核函數以及多層感知機核函數5種。由于高斯徑向基核函數具有良好的泛化性，所以本文算法中選擇高斯核函數。

作為一種具有較強魯棒性的非參數估計方法，支持向量機回歸在電機設計優化中已經得到了成功的應用。彭春華等通過支持向量機算法建立風電機出力與運行參數之間的非線性擬合模型，并基于此模型和風速的變化對風力機槳距角進行優化進而實現了風電機出力最大化［7］。王群京等介紹了支持向量機在電機設計中的一些應用，并對其在永磁球形步進電動機中的應用前景進行了展望［8］。支持向量機回歸建模除了核函數的選擇，其內容還包括容量誤差的選擇、損失函數的選擇以及與核有關的參數的選擇等。

2.2 樣本空間建立

參數優化的第一步工作是產生用于非線性電磁建模的輸入輸出樣本數據。本文中，輸入為設計變量:永磁體厚度、偏心距、極弧系數與氣隙長度，輸出為目標函數:電機齒槽轉矩。4個設計變量各有5個取值，總共有625次實驗。為縮短耗時，采用正交實驗設計方法選取實驗數據。

正交實驗利用設計變量各水平之間的互相均勻搭配，使方案產生的數據點在設計變量空間均勻分布，進而較全面地反映設計變量對系統性能特征的影響規律。通過初步的實驗可以確定實驗中各變量合理的取值范圍:極弧系數0.6～0.85(無量綱)，偏心距1 ～5mm，氣隙長度0.6 ～1.2mm，磁極厚度3.5～8mm，依據因數個數和水平個數選擇正交表，將各組方案依次輸入Ansoft，進行電磁場求解，得到的實驗結果即可構成SVM算法的樣本空間。實驗中各變量的取值如表2所示。

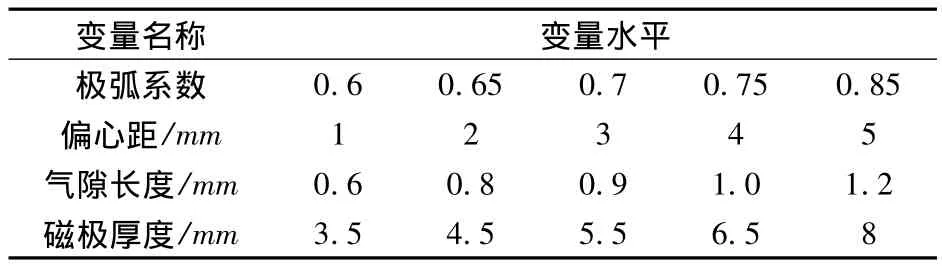
表2 變量水平表

2.3 SVM數學模型建立

最優分類超平面就是SVM算法的數學模型，可以用核函數的代數和表示此超平面:

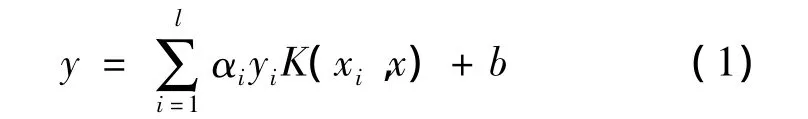
式中:αi為25個樣本點中作為支持向量的樣本點所對應的拉格朗日常數;K(xi，x)為核函數，支持向量個數則由l表示。從式(1)可看出，欲得到擬合超平面的表達式，需要求取相應的支持向量以及αi。安裝libsvm工具箱(林智仁教授等編寫)后可以通過MATLAB對模型進行求解。懲罰參數C和核函數參數g是SVM模型的兩個關鍵參數，其值選取會對支持向量機的預測效果產生影響，為得到某種意義下的最優參數，往往采用交叉驗證的的思想［9］，可以有效地減少過學習和欠學習狀態發生的情況。利用網格搜索算法編寫程序，得到C和g的最佳取值，多次調試后得到該問題中的最優參數為C=318.793 2，g=0.03，進而可以得到目標函數的數學模型。

SVM模型預測值與實際值之間的對比如圖3所示，三角形代表SVM模型預測的數據，圓圈代表原始數據。

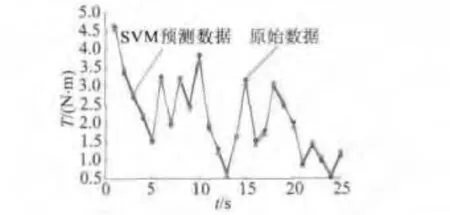
圖3 原始數據曲線與擬合數據曲線

2.4 粒子群算法尋優

1995年，Eberhart和Kennedy提出一種群體智能優化算法——粒子群優化(PSO)算法，它的誕生起源于對鳥類覓食過程的研究［10］。PSO算法中，適應度函數對應鳥群與食物之間的距離，每個粒子對應鳥群中的一只鳥，一旦鳥類完成覓食，就代表粒子通過改變自身空間位置而使適應度函數達到了最小值。粒子具有速度、位置以及適應度值三個特征，每個粒子都對應優化問題的一個潛在最優解。粒子的位置和速度是尋優過程中的兩個決定性因素，其中個體位置通過跟蹤個體極值和群體極值實現更新，而粒子速度則決定了粒子移動的方向和距離，它會隨自身及其他粒子的移動經驗進行動態調整，從而實現個體在可解空間中的尋優。

對于D維全局優化問題，X=(X1，X2，…Xn)是由n個粒子組成的種群，Xi=(xi1，xi2，…xiD)T代表第i個粒子在搜索空間中的位置，也代表問題的一個潛在解，根據目標函數表達式可計算出每個Xi對應的適應度值。Vi=(Vi1，Vi2，…，ViD)T為第 i個粒子的速度，Pi=(Pi1，Pi2，…PiD)T為粒子個體極值，而Pg=(Pg1，Pg2，…，PgD)T為種群的全局極值。

該粒子迭代后位置:

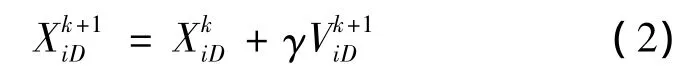
而其迭代后的速度:

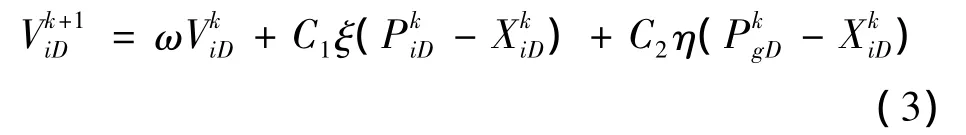
式中:k為迭代數;ω為慣性權重;ξ和η為［0，1］內的隨機數;C1、C2為加速常量，分別代表粒子自我認知系數和社會認知系數;γ為速度更新約束因子。PSO算法尋優過程如圖4所示。

對于本文的優化問題，將每個設計變量的取值范圍作為約束條件，4 個設計變量(x1，x2，x3，x4)作為一個粒子的坐標，SVM預測結果作為適應度函數，利用PSO算法對其進行優化，迭代數為200，種群數量為20，C1和 C2分別設為1.5和1.7，經 PSO尋優后，可得最優點的變量取值:(0.85，4.522 6，0.6，8)。

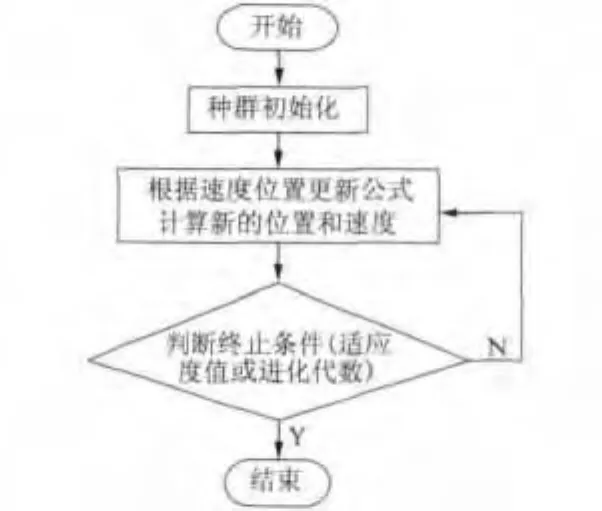
圖4 PSO算法流程圖

將優化后的方案代入Ansoft軟件，仿真出的齒槽轉矩如圖5所示。由圖5可看出，優化后齒槽轉矩為0.314 N·m，相比之前大大減小，仿真結果驗證了模型的準確性。

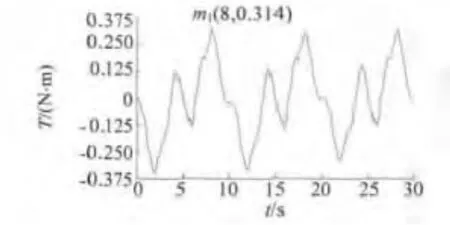
圖5 優化后的齒槽轉矩曲線

3 結 語

本文從影響永磁同步電機齒槽轉矩的因素出發，采用支持向量機方法對其進行回歸建模，在此基礎上利用粒子群算法對電機的極弧系數、偏心距、氣隙長度以及磁極厚度進行優化，通過相對較少的計算，得到了一組使齒槽轉矩最小的參數:極弧系數為0.85，偏心距近似為 4.5mm，氣隙長度為 0.6mm，磁極厚度為8mm。從優化的有限元仿真結果可知，電機的齒槽轉矩由原先的3.06 N·m變為0.314 N·m，大大減小，計算和仿真結果證明了支持向量機在永磁同步電機齒槽轉矩優化中的可行性，為電機其他參數的優化過程提供了有效的參考。

［1］楊玉波，王秀和，丁婷婷，等.極弧系數組合優化的永磁電機齒槽轉矩削弱方法［J］.中國電機工程學報，2007，26(6):8－11.

［2］秦虹.永磁無刷直流電動機齒槽轉矩的削弱［J］.電機技術，2009(12):10－13，18.

［3］周俊杰，范承志，葉云岳.盤式永磁電機齒槽轉矩的分析與抑制［J］.機電工程，2009，26(2):79－81.

［4］鄧秋玲，黃守道，劉婷，等.永磁電機齒槽轉矩的研究分析［J］.湖南大學學報(自然科學版)，2011，38(3):56－59.

［5］王廣生，黃守道，高劍.基于Ansoft軟件設計分析內置式永磁同步電動機［J］.微電機，2011，44(2):70－73.

［6］張曉宇，王曉遠.減少齒槽轉矩的無刷直流電機優化設計［J］.微電機，2013，46(1):24－27，40.

［7］彭春華，相龍陽，劉剛，等.基于支持向量機和微分進化算法的風電機優化運行［J］.電網技術，2012，36(4):57－62.

［8］王群京，鞠魯峰，錢喆，等.支持向量機理論及其在復雜電機設計中的應用［J］.微特電機，2010，(3):67－70.

［9］CAMPBELL C.Algorithmic approaches to training support vector machines:A survey［C］//Proceedings of E－SANN2000.Belgium:D－Facto Publications，2000:27－36.

［10］范堅堅，吳建華，黎憲林，等.永磁同步電動機磁鋼的多目標粒子群算法優化［J］.電機與控制學報，2009，13(2):173－178.