雙三相永磁同步電動機交互磁飽和模型仿真研究

何新薈，辛小南，齊 歌

(鄭州大學，河南鄭州450001)

0 引 言

與傳統三相永磁同步電動機相比，雙三相永磁同步電動機具有以下優點:用低壓器件實現大功率輸出、減少空間諧波磁勢、減少噪聲、提高效率、實現可靠性冗余運行［1］。目前研究較多的雙三相電機，兩套繞組呈30°夾角。但在這種連接方式下，兩套繞組之間存在耦合，對電機的控制性能會產生不利影響。為消除耦合的不利因素，本文采用兩套繞組呈180°夾角的雙三相電機［2］。同時，通常所采用的基于派克變換的d，q軸等效電路模型認為磁路是線性的，即模型中的電感值為常量［1］，從而忽略了電機帶負載時磁場飽和的影響。而實際上，由于磁滯影響，d，q軸均存在磁場飽和現象，兩軸之間還存在交互磁飽和，所以這種不考慮飽和的電機模型是不夠精確的。為改進這種模型，考慮交互磁飽和影響，本文利用MATLAB/Simulink搭建了基于內插外推法的飽和模型，并用仿真實驗來驗證飽和模型的有效性。

1 考慮交互磁飽和電機模型

對于兩套繞組呈180°夾角的雙三相電機，兩套繞組的空間排列關系如圖1所示。采用此繞組分布，可以有效削弱各個相繞組之間的相互影響，增大相繞組自感，減小相繞組之間的互感，尤其是兩套三相繞組之間的互感，有利于雙三相電機的解耦控制［2］。

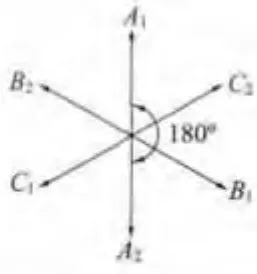
圖1 雙三相永磁同步電動機定子繞組分布

建立在六相靜止坐標系上的數學模型復雜，不利于分析。為簡化電機模型，利用轉換矩陣T［3－4］，得到兩相靜止α－β坐標系下的數學模型，然后通過派克變換，得到兩相旋轉d－q坐標系下的數學模型。

將電機模型從六相靜止坐標系轉換到α－β坐標系的轉換矩陣T為:

d－q坐標系下電壓及磁鏈方程如下:

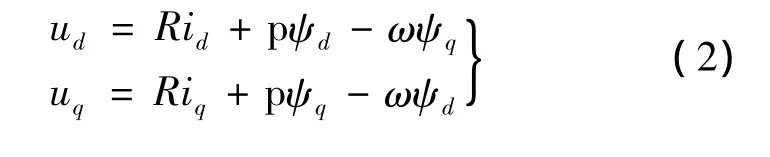
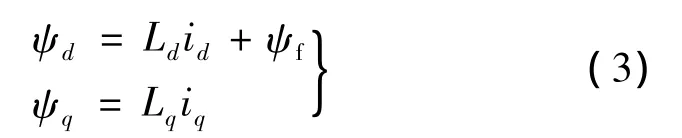
電磁轉矩及運動方程如下:

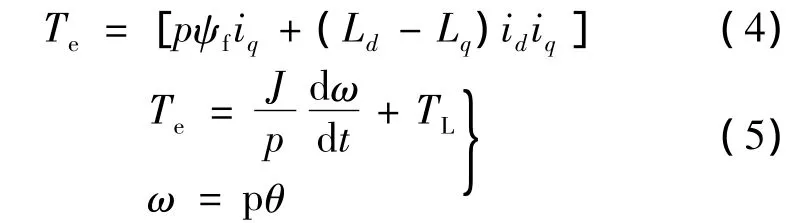
式中:ud，uq為d，q軸定子電壓分量;R為定子電阻;id，iq為 d，q軸電流分量;ψd，ψq為 d，q 軸磁鏈分量;Ld，Lq為 d，q軸電感分量;ψf為永磁體磁鏈;為微分算子;p為極對數;TL為負載轉矩;J為轉動慣量;ω為機械角速度。

1.1 d，q 軸交互磁飽和

考慮交互磁飽和法，是在磁鏈法的基礎上，考慮了id，iq對 Ld，Lq的交互影響。故 ψd不僅與 id有關，還受到iq的影響;ψq也同時受到 id，iq的影響。此時磁鏈方程:

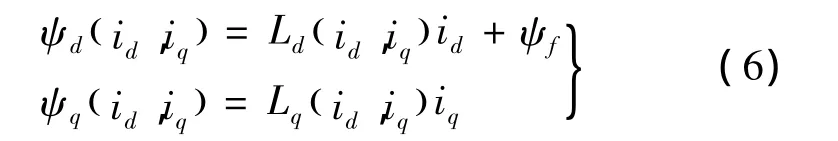
將式(6)代入式(2)、式(4)中，得考慮磁飽和的電壓方程及電磁轉矩方程:

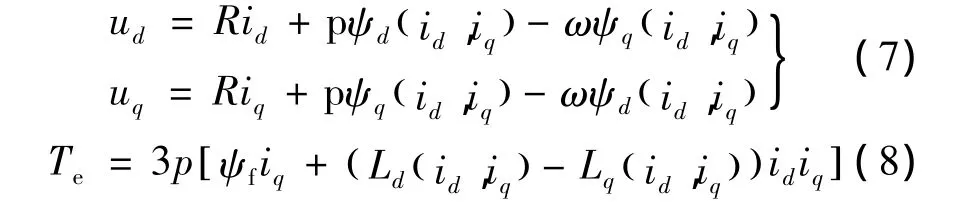
為分析 id，iq對 Ld，Lq的交互影響，文獻［2］利用有限元法得到的Ld，Lq與id，iq的非線性關系，如圖2所示。

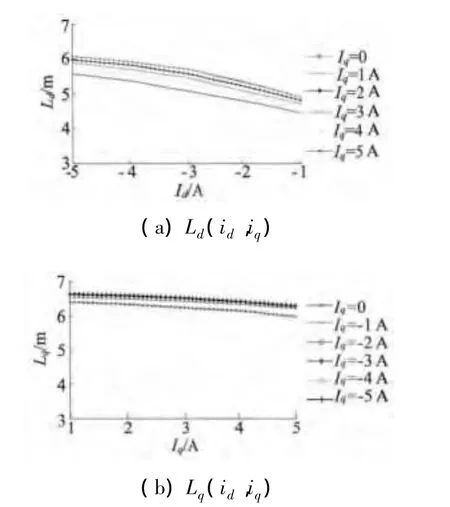
圖2 d，q軸電感

電機空載時，輸入功率全部轉化為電機內部損耗;穩態運行時，電機內部損耗基本不變，故Ld，Lq可近似為常值。當電機負載逐步增大時，輸入功率包含電機內部損耗和輸出功率，由圖可知，id負向增加，去磁作用明顯，磁路飽和程度下降，磁導率變大，故Ld增大。考慮交互磁飽和的影響，iq的增加使得d軸磁路飽和程度稍有增加，故Ld有所下降。同時，Lq隨著iq的變化不明顯，iq增加，Lq略有減小;考慮交互磁飽和的影響，id的負向增加，使得q軸磁路受到影響，飽和程度下降，故Lq隨著id負向增加而增大。

1.2 考慮交互磁飽和仿真模型

為反映圖2中d，q軸交互磁飽和，利用MATLAB/Simulink建立雙三相永磁同步電動機的仿真模型，如圖3所示。模型輸入為滿足圖1相角關系的雙三相電壓、負載轉矩TL和永磁體磁鏈ψf，輸出為雙三相定子電流、電磁轉矩Te和轉速n。

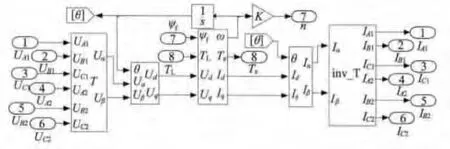
圖3 雙三相永磁同步電動機仿真模型

根據式(6)、式(7)，可得d－q坐標系下電機磁鏈和電壓模塊，模塊中id，iq的計算需要使用Ld，Lq的值，而電機的電機參數Ld，Lq與電機的運行狀態有關:當電機空載時，Ld，Lq值是常量;當電機帶負載運行時，由于磁飽和影響，Ld，Lq由電流 id，iq決定(見圖2)。本文采用Switch模塊以TL為條件來實現這種轉換:當 TL=0 時，Ld=C1，Lq=C2，C1，C2為常量;當 TL＞0 時，Ld=Ld1，Lq=Lq1，而 Ld1，Lq1為滿足圖2 的函數:Ld1=f1(id，iq)，Lq1=f2(id，iq)。

由于d，q軸電感與電流呈非線性關系，難以寫出由 id，iq求解 Ld1，Lq1的解析式 f1，f2。而內插外推法［5］可以通過已觀測點數據來估算區域內或區域外未觀測點的數據，且效率高、估值準確。為計算Ld1，Lq1的值，本文利用 MATLAB/Simulink中 Lookup Table(2－D)模塊，采用兩變量的內插外推法建立了 Ld1，Lq1的計算模塊。

2 仿真驗證

為驗證考慮交互磁飽和仿真模型的有效性，將其與不考慮飽和的電機模型在MATLAB/Simulink環境下進行仿真比較。雙三相繞組均采用Y接法，主要仿真參數:額定電流5 A，額定電壓36 V，額定轉速400 r/min，Ld=4.940 3 mH，Lq=6.400 5 mH，p=5，J=0.001 kg·m2，ψf=0.150 37 Wb，TN=5.5 N·m，R=0.419 Ω。

圖4分別表示雙三相永磁同步電動機不飽和、飽和模型定子電流d，q軸分量在負載轉矩TL躍變時的變化曲線，圖中虛線表示不飽和模型的id_unsat、iq_unsat，實線表示飽和模型的 id_sat，iq_sat。t=0.3 s 時，TL從0躍變為5.5 N·m。此時，定子電流d軸分量負向增大。對于飽和模型，考慮到交互磁飽和作用，d軸去磁作用明顯，磁場飽和程度降低，故飽和模型的id_sat絕對值明顯小于不飽和模型的id_unsat的絕對值。同時，定子電流q軸分量增大，由于受到d軸電流的影響，故飽和模型的iq_sat與不飽和模型的iq_unsat相比，增大不明顯。

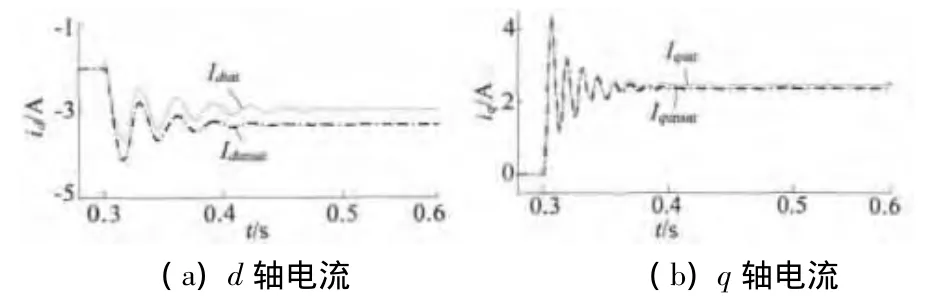
圖4 定子d，q軸電流分量

圖5為負載轉矩躍變時，飽和電機模型的仿真結果。t=0 s時，電機空載，經過0.14 s短時波動達到穩定運行狀態，定子電流幅值為2.04 A，電磁轉矩為0，轉速為額定轉速400 r/min。t=0.3 s時，負載轉矩躍變為5.5 N·m，經過0.14 s短暫波動，定子電流幅值穩定在3.825 A，電磁轉矩達到額定負載轉矩，轉速恢復為額定轉速。

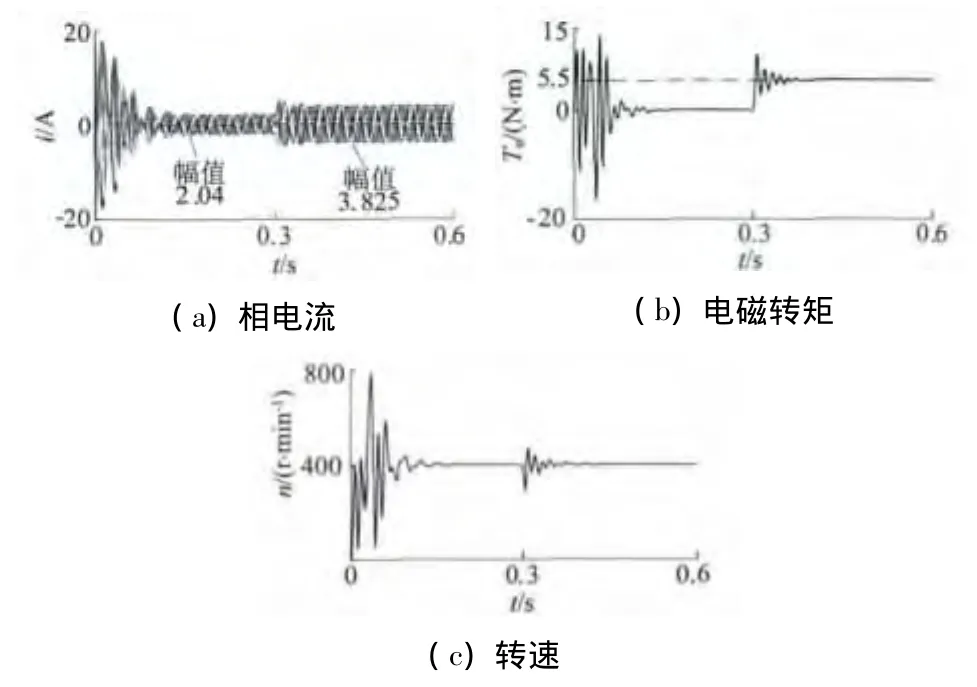
圖5 電機飽和模型相電流、電磁轉矩和轉速

3 結 語

本文通過有限元分析獲得電機d，q軸電感與電流的非線性關系，分析了雙三相永磁同步電動機d，q軸交互磁飽和的機理。考慮交互磁飽和仿真模型，能夠準確反映雙三相永磁同步電動機磁路飽和狀態下的運行特性，彌補了不飽和模型的不足。本文所采用的建模方法簡單直觀，同樣適用于其他非線性模型的建立。

［1］李崇堅.交流同步電機調速系統［M］.北京:科學出版社，2006.

［2］齊歌.雙三相永磁同步電動機交互飽和模型與特性研究［D］.武漢:華中科技大學，2010.

［3］黃進.p對極n相對稱系統的變換理論［J］.電工技術學報，1995，(1):53－57.

［4］ZHAO Yifan，LIPO T A.Space vector PWM control of dual three－phase induction machine using vector space decomposition［J］.IEEE Transactions on industry applications，1995，31(5):1100－1109.

［5］熊鄴，方大綱，劉鐵軍.電磁場數值計算中的內插和外推［J］.電波科學學報，2002，17(4):325－329.

［6］楊金波.雙三相永磁同步電機驅動技術研究［D］.哈爾濱:哈爾濱工業大學，2011.

［7］李景燦，廖勇.考慮飽和及轉子磁場諧波的永磁同步電機模型［J］.中國電機工程學報，2011，31(3):60－66.

［8］景巍，譚國俊，葉宗彬.考慮磁場飽和效應的凸極同步電動機建模［J］.電機與控制學報，2010，14(10):94－99.