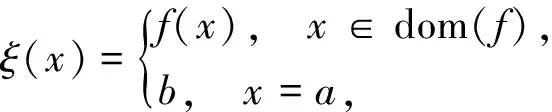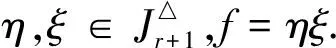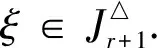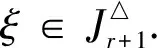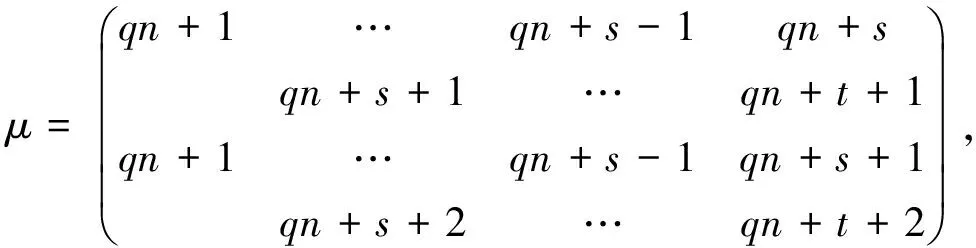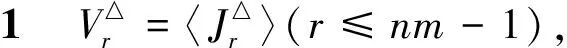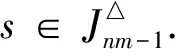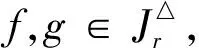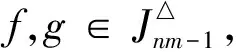保E且嚴(yán)格保序部分一一變換半群的秩

龍偉鋒, 徐 波, 游泰杰, 汪繼秀

(1. 貴州師范大學(xué) 數(shù)學(xué)與計算機科學(xué)學(xué)院, 貴州 貴陽 550001; 2. 湖北文理學(xué)院 數(shù)學(xué)與計算機學(xué)院, 湖北 襄陽 441053)

在半群代數(shù)的研究中,變換半群的秩一直是研究的重要課題之一,關(guān)于它的研究已經(jīng)有了許多成果[1-6].

通常,一個有限變換半群S的秩定義為:rankS={min|A|:A?S,〈A〉=S}.如果S是由冪等元集E生成的,那么S的冪等元秩定義為:irankS={min |A|:A?E,〈A〉=S}.顯然有rankS≤irankS.

設(shè)[n]={1,2,…,n}并賦予自然序,In與Sn分別表示[n]上的對稱逆半群和對稱群.設(shè)α∈In,若?x,y∈dom(α),x≤y蘊含xα≤yα,則稱α為保序部分一一變換.令POIn={α∈InSn:?x,y∈dom(α),x≤y蘊含xα≤yα},則POIn是In的一個逆子半群,稱之為保序部分一一變換半群.文獻[1]刻畫了POIn的秩與表示.

設(shè)X為有限集合,E為X上的等價關(guān)系且IX為X上的對稱逆半群.令

IE*(X)={f∈IX:?x,y∈dom(f),(x,y)∈E

當(dāng)且僅當(dāng)(f(x),f(y))∈E},

則IE*(X)為IX的逆子半群,稱為保E*關(guān)系部分一一變換半群.文獻[2]討論了它的Green關(guān)系與秩.

令X為有限集合,E為X上的等價關(guān)系且IE*(X)為X上的保E*關(guān)系部分一一變換半群.設(shè)f∈IE*(X)且dom(f)={a1,a2,…,ar},其中a1

任取x,y∈X,若x≤y,定義[x,y]={z∈X:x≤z≤y}.對于一般情形,即對任意的有限全序集X和X上的任意等價關(guān)系,很難描述半群SPOIE(X)的秩.因此,先考慮一種特殊情形.本文總是假設(shè)X={1,2,…,nm}(n≥3,m≥2)為全序集,E為X上的等價關(guān)系,滿足

E=(A1×A1)∪(A2×A2)∪…∪(Am×Am),

其中,Ai=[(i-1)n+1,in],i=1,2,…,m.本文在上述全序集與等價關(guān)系下,討論了SPOIE(X)的秩.

1 預(yù)備知識

為了敘述方便,在SPOIE(X)上引入下面的二元關(guān)系,?f,g∈SPOIE(X),定義

(f,g)∈L△當(dāng)且僅當(dāng)im(f)=im(g),

(f,g)∈R△當(dāng)且僅當(dāng)dom(f)=dom(g),

(f,g)∈H△當(dāng)且僅當(dāng)im(f)=im(g)且dom(f)=dom(g),

(f,g)∈J△當(dāng)且僅當(dāng)|im(f)|=|im(g)|,

則H△、L△、R△、J△都是SPOIE(X)上的等價關(guān)系,易見H△?L△?J△,H△?R△?J△.對1≤r≤nm-1,記

文中未說明的符號與概念請參看文獻[9].

2 主要結(jié)果與證明

首先給出本文的主要結(jié)果.

定理1rank SPOIE(X)=nm.為了完成定理1的證明,下面給出若干引理.

情形1|Ap∩dom(f)|=n-1,不妨設(shè)

其中a1

a1

f(a1)

f(aj+1)<…

以下分3種情況討論.

則有

2)i

f∣Ap=ψφ=η∣Aqξ∣Ap=

此外考慮當(dāng)x∈dom(f)Ap時,ηξ(x)=η(f(x))=f(x).故f=ηξ.

3)i>j.證明類似于2)的證明.

情形2|Ap∩dom(f)|≤n-2,設(shè)

其中a1

設(shè)s是在1,2,…,t中使得f(as)≠qn+s的最小整數(shù),則f(as)≥qn+s+1.下面分3種情況一一討論.

1)s

下證f=η2η1ξ.由ξ、η1、η2的定義,易驗證dom(η2η1ξ)=dom(f)且

f∣Ap=νμθ=η2∣Aqη1∣Aqξ∣Ap=

2)s=i+1.令

下證f=η2η1ξ.由ξ、η1、η2的定義,易驗證dom(η2η1ξ)=dom(f)且

f∣Ap=σρθ=η2∣Aqη1∣Aqξ∣Ap=

3)s>i+1,證明類似于2)的證明.

1) 當(dāng)j∈{1,2,…,n-1},

gij:X{in+j}→X{in+j+1},

2) 當(dāng)j=n時

gin:X{(i+1)n}→X{in+1},

由gi1,gi2,…,gin的定義,易驗證對?i∈{1,2,…,m},都有im(gij)=dom(gij+1)(j∈{1,…,n-1}),im(gin)=dom(gi1).

引理2令A(yù)={gij:1≤i≤m,1≤j≤n},則SOPIE(X)=〈A〉.

由引理2及有限半群秩的定義可得如下推論:

推論2rank SOPIE(X)≤nm.

[1] Fernandes V H. The monoid of all injective order preserving partial transformation on a finite chain[J]. Semigroup Forum,2001,62(2):178-204.

[2] 龍偉鋒,游泰杰,龍偉芳,等. 保E*關(guān)系的部分一一變換半群[J]. 西南大學(xué)學(xué)報:自然科學(xué)版,2013,35(4):63-66.

[3] Fernandes V H. The monoid of all injective orientation preserving partial transformations on a finite chain [J]. Commun Algebra,2000,28(7):3401-3426.

[4] 徐波,馮榮權(quán),高榮海. 一類變換半群的秩[J]. 數(shù)學(xué)實踐與認(rèn)識,2010,40(8):222-224.

[5] Zhao P. On the ranks of certain semigroups of orientation preserving transformations[J]. Commun Algebra,2011,39(11):4195-4205.

[6] 高榮海,徐波. 核具有連續(xù)橫截面的保序變換半群的秩[J]. 西南師范大學(xué)學(xué)報:自然科學(xué)版,2013,38(4):18-24.

[7] 高榮海. 具有穩(wěn)定子集的有限奇異變換半群的冪等元生成元[J]. 四川師范大學(xué)學(xué)報:自然科學(xué)版,2010,33(6):778-783.

[8] 蘭丙申,喻秉鈞. 擬純正半群的E-酉擬純正蓋[J]. 四川師范大學(xué)學(xué)報:自然科學(xué)版,2012,35(5):581-584.

[9] Howie J M. An Introduction to Semigpoup Theory [M]. London:London Academic Press,1976.

[10] 高榮海,徐波. 關(guān)于保序壓縮奇異變換半群的秩[J]. 山東大學(xué)學(xué)報:理學(xué)版,2011,46(6):4-7.

[11] 趙平,游泰杰,徐波. 半群CPOn的秩[J]. 西南大學(xué)學(xué)報:自然科學(xué)版,2011,33(6):106-110.

[12] 趙平. 半群PK-(n,r)的冪等元秩[J]. 西南師范大學(xué)學(xué)報:自然科學(xué)版,2008,33(8):9-12.

[13] 高榮海. 關(guān)于一類純正半群的冪等元秩[J]. 華南師范大學(xué)學(xué)報:自然科學(xué)版,2013,45(3):33-35.

[14] 楊秀良. 嚴(yán)格部分變換半群的冪等元秩[J]. 數(shù)學(xué)研究與評論,2000,20(30):441-446.

[15] 高榮海. 單調(diào)壓縮部分變換半群的秩[J]. 常熟理工學(xué)院學(xué)報:自然科學(xué)版,2013,27(2):35-38.

[16] 鄒定宇,裴恵生,王世飛. TE(X)的由冪等元生成的子半群[J]. 信陽師范學(xué)院學(xué)報:自然科學(xué)版,2004,17(2):125-128.