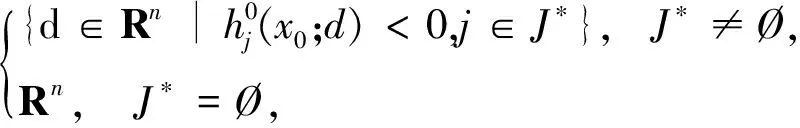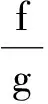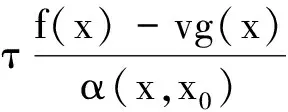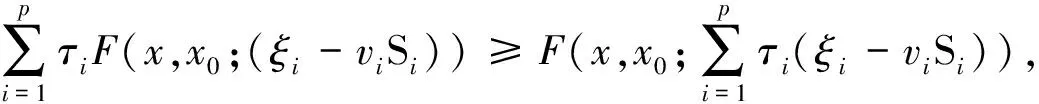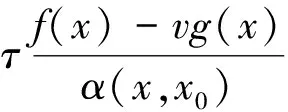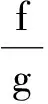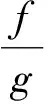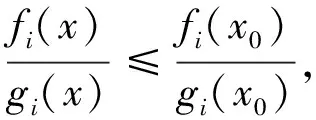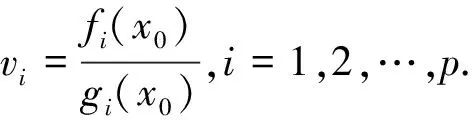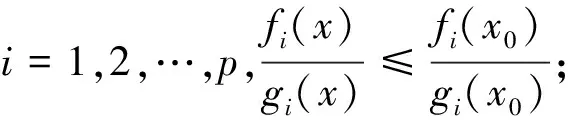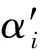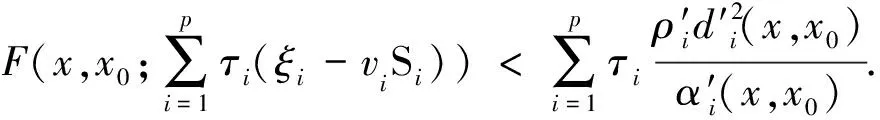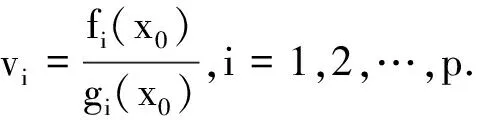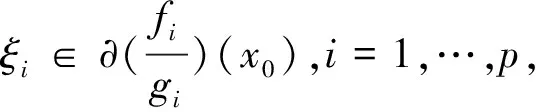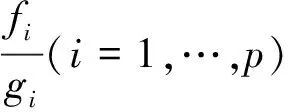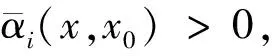一類不可微多目標分式規劃問題的最優性條件
張曉敏, 吳澤忠
(成都信息工程學院 數學學院, 四川 成都 610225)
1 預備知識
在F-凸[1]和ρ-凸[2]的基礎上,V. Preda[3]提出(F,ρ)-凸的概念,并獲得一些結果,是F- 凸和ρ- 凸的擴展;Z. A. Liang等[4]提出(F,α,ρ,d)- 凸的概念,進一步擴展了(F,ρ)-凸;文獻[5]在(F,α,ρ,d)-凸的基礎上,提出了廣義(F,α,ρ,d)- 凸的概念.
在不同的凸性假設下,已得到一些成果[1,3,6-19],但是在微分概念基礎上的非線性規劃理論和算法不再適用于非光滑最優化問題,對于非光滑最優化問題也已得出一些結論[20-31]. 本文在非光滑(F,α,ρ,d)-凸函數的基礎上給出廣義非光滑(F,α,ρ,d)- 凸函數的定義,在這些弱化的凸性的假設下得出一類不可微多目標分式規劃問題的最優性條件.
考慮多目標分式規劃問題(MFP)
其中,fi:Rn→R,gi:Rn→R,i=1,2,…,p,hj:Rn→R,j=1,2,…,m,都是局部Lipschitz函數,并假設在Rn上,fi(x)≥0,gi(x)>0,i=1,2,…,p.稱S={x∈Rn|hj(x)≤0,j=1,2,…,m}為(MFP)的可行集.
本節中約定?x,y∈Rn,x>y?xi>yi,i=1,2,…,n;x≥y?xi≥yi,i=1,2,…,n[13].
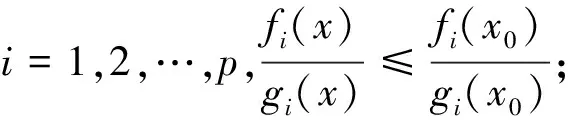
定義3[30]如果f:Rn→R在x∈Rn上是局部Lipschitz函數,則f在x∈Rn沿方向d∈Rn的廣義導數,記為f0(x;d),定義為
定義4[30]設f:Rn→R是局部Lipschitz函數,f在x∈Rn處的廣義Clarke梯度定義為?f(x),記?f(x)={ξ∈Rn:f0(x;d)≥ξTd,?d∈Rn}.
定義5[30-31]設f:Rn→R是Lipschitz的,d∈Rn,稱f在x∈Rn處正則,如果f在x∈Rn處是方向可微的,且f0(x;d)=f′(x;d).
定義6[3]稱函數F:Rn×Rn×Rn→R為次線性函數,如果?x,x0∈X0有
F(x,x0;a1+a2)≤F(x,x0;a1)+
F(x,x0;a2), ?a1,a2∈Rn,
F(x,x0;αa)=αF(x,x0;a),
?α∈R,α≥0, ?a∈Rn.
特別地
F(x,x0;0)=F(x,x0;0a)=0×F(x,x0;a),
0∈R, 0∈Rn, ?a∈Rn.
定義7[29]設F:Rn×Rn×Rn→R是次線性函數,函數f:Rn→R在x0∈Rn是局部Lipschitz的,α:Rn×Rn→R+{0},ρ∈R,d:Rn×Rn→R.稱函數f在x0是非光滑(F,α,ρ,d)-凸函數,如果對?ξ∈?f(x0),對所有的x∈Rn有
f(x)-f(x0)≥F(x,x0;α(x,x0)ξ)+ρd2(x,x0).
如果函數f在Rn上每一點都是非光滑(F,α,ρ,d)-凸函數,則稱f在Rn上是非光滑(F,α,ρ,d)-凸函數.
定義8如果f(x) 定義9如果f(x)≤f(x0)?F(x,x0;α(x,x0)ξ)≤-ρd2(x,x0),則稱f在x0∈X是非光滑強(F,α,ρ,d)-偽凸函數. 定義10如果f(x)≤f(x0)?F(x,x0;α(x,x0)ξ)<-ρd2(x,x0),則稱f在x0∈X是非光滑弱嚴格(F,α,ρ,d)-偽凸函數. 在點x0∈Rn定義集合J*={j∈J∣hj(x0=0)},J={1,2,…,m}. 約束規格在點x0,Ω0≠?. 引理1[30]設f1,f2:Rn→R在x處是Lipschitz的,如果f1(x)≥0,f2(x)>0,f1-f2在x處正則,則 證明由f-vge:=(f1-v1g1,…,fp-vpgp)在x0∈X是非光滑(F,α,ρ,d)-偽凸函數得 fi(x)-vigi(x) 又由τ>0,αi(x,x0)>0, ? ? 定理2設(x0,τ,λ)∈Rn×Rp×Rm滿足 λjhj(x0)=0,j=1,2,…,m, (2) τ>0,λ≥0, (3) 對所有的i=1,2,…,p,fi(x)-vigi(x)≤fi(x0)-vigi(x0); 對其中某些k,fi(x)-vigi(x) (5) 又h在x0∈X是非光滑(F,α″,ρ″,d″)-凸函數,有 (6) 所以 (7) (7)+(8)式得 即 那么x0是(MFP)的有效解. 證明只需改變定理2的證明中的關于函數h的部分. 由h在x0∈X是非光滑(F,α″,ρ″,d″)-偽凸函數(或非光滑弱嚴格(F,α″,ρ″,d″)-偽凸函數),及hj(x)≤0,hj(x0)=0得hj(x)≤hj(x0),故 即(6)式,余下證明與定理2相同. (9) 如果fi、-gi(i=1,…,p)在x0是非光滑(F,α1i,ρ1i,d1i)-凸函數,hj(j=1,…,m)在x0是非光滑強(F,α2j,ρ2j,d2j)-偽凸函數,且 (11) 假設x0不是(MFP)的有效解,則存在(MFP)的有效解x使得 至少有一個不等式嚴格成立. 至少有一個不等式嚴格成立. 又τ>0,所以 由F的次線性性得 由hj(j=1,…,m)在x0是非光滑強(F,α2j,ρ2j,d2j)-偽凸函數,及hj(x)≤0,hj(x0)=0,有hj(x)≤hj(x0),故 又λj≥0,α2j(x,x0)>0及F的次線性性可得 即 (12)+(13)式得 顯然與(10)式矛盾. 證明只需改變定理4證明中的關于函數h的部分. 由hj(j=1,…,m)在x0是非光滑弱嚴格(F,α2j,ρ2j,d2j)-偽凸函數,及hj(x)≤0,hj(x0)=0,有hj(x)≤hj(x0),故 又λj≥0,α2j(x,x0)>0及F的次線性性可得 即得(13)式,其余部分的證明與定理4相同. 致謝成都信息工程學院引進人才項目(KYTZ201203)和成都信息工程學院中青年學術帶頭人科研基金(J201218)對本文給予了資助,謹致謝意. [1] Gulati T R, Islam M A. Sufficiency and duality in multi-objective programming problems involving generalizedF-convex functions[J]. J Math Anal Appl,1994,183:181-195. [2] Vial J P. Strong and weak convexity set and functions[J]. Math Oper Res,1983,8:231-259. [3] Preda V. On efficiency and duality for multi-objective programs[J]. JMAA,1992,166:365-377. [4] Liang Z A, Huang H X, Pardalos P M. Optimality conditions and duality for a class of nonlinear fractional programming problems[J].J Opt Theory Appl,2001,110:611-619. [5] 吳澤忠,李澤民. 廣義(F,α,ρ,d)-凸條件下多目標規劃問題的最優性充分條件[J]. 經濟數學,2002,19(4):90-94. [6] Weir T , Mond B. Generalized convexity and duality in multi-objective programming[J]. Bull Austral Math Soc,1989,39:287-299. [7] Egudo R. Efficiency and generalized convex duality for multi-objective programs [J]. J Math Anal Appl,1989,138:84-94. [8] 曾德勝,吳澤忠. 一類多目標分式規劃問題的最優性條件[J]. 四川大學學報:自然科學版,2006,43(4):751-756. [9] 吳澤忠,鄭豐華. 一類非線性分式規劃問題的最優性條件和對偶[J]. 四川師范大學學報:自然科學版,2007,30(5):594-597. [10] 吳傳平. 多目標數學規劃解的一些新的充要條件[J]. 重慶文理學院學報:自然科學版,2011,30(4):9-11. [11] 李瑞華,主雪梅. 廣義凸規劃問題的最優性條件[J]. 綿陽師范學院學報:自然科學版,2010,2(29):15-18. [12] 李動鋒,邱根勝. 一種新廣義凸多目標分式規劃的最優性充分條件[J]. 純粹數學與應用數學,2009,25(4):807-815. [13] 彭再云,雷鳴,劉亞威,等. 一類可微凸多目標分式規劃的最優性條件[J]. 重慶交通大學學報:自然科學版,2009,28(1):156-158. [14] 吳澤忠. (F,α,ρ,d)-凸性下一類多目標分式規劃問題的最優性條件和對偶[J]. 四川大學學報:自然科學版,2009,46(6):1623-1627. [15] 江維瓊,吳春. 廣義(F,α,ρ,d)-凸性條件下多目標分式規劃問題的K-T條件及對偶[J]. 黃岡師范學院學報,2006,26(3):11-27. [16] Cambini A, Martein L. Generalized Convexity and Optimization[M]. Berlin,Heideberg:Spriner-Verlag,2008:78-81. [17] 林銼云,董加禮. 多目標優化的方法與理論[M]. 長春:吉林教育出版社,1992:1-449. [18] 曾德勝,吳澤忠. (F,α,ρ,d)-凸和廣義(F,α,ρ,d)-凸性下一類多目標規劃問題的對偶[J]. 四川師范大學學報:自然科學版,2006,29(1):63-66. [19] 張曉敏,吳澤忠. (F,α,ρ,d)-凸和廣義(F,α,ρ,d)-凸條件下一類多目標規劃問題的對偶[J]. 成都信息工程學院學報,2012,27(3):318-325. [20] Liu J C. Optimality and duality for generalized fractional programming involving nonsmooth (F,P)-convex functions[J]. Comput Math Appl,1996,32:91-102. [21] 羅勇,姚元金. 一類非凸非光滑多目標分式規劃的最優性條件[J]. 湖北民族學院學報:自然科學版,2009,27(4):398-402. [22] 顏麗佳. 非光滑(F,α,ρ,d)-凸函數的多目標分式規劃最優性條件[J]. 西華師范大學學報:自然科學版,2006,27(4):361-364. [23] 顏麗佳. 關于非光滑(F,α,ρ,d)-凸函數的多目標分式規劃的對偶性[J]. 西華師范大學學報:自然科學版,2008,29(1):24-28. [24] Zhao K Q, Tang L P, Yang X M. Optimality and duality for a class of non-smooth optimization problems[J]. OR Transactions,2010,14(2):45-54. [25] 趙克全,唐莉萍. 一類不可微多目標分式規劃問題的最優性條件[J]. 重慶師范大學學報:自然科學版,2010,27(4):1-4. [26] 唐莉萍,蔣華, 趙克全,等. 一類非光滑規劃問題的混合對偶[J]. 四川師范大學學報:自然科學版,2011,34(1):34-37. [27] Zheng X J, Cheng L. Minimax fractional programming under non-smooth generalized (s,ρ,θ) -d-univexity[J]. J Math Anal Appl,2007,328:676-689. [28] 姜艷,張慶祥. 一類不可微凸多目標規劃解的最優性充分條件[J]. 延安大學學報:自然科學版,2010,29(1):17-21. [29] Liu S M, Feng E M. Optimality conditions and duality for a class of nondifferentiable multi-objective fractional programming problems[J]. J Glob Optim,2007,38:653-666. [30] Clarke F H. Optimization and Nonsmooth Analysis[M]. New York:Wiley-Interscience,1983. [31] 趙克全,羅杰,唐莉萍. 一類非光滑規劃問題的最優性條件[J]. 重慶師范大學學報:自然科學版,2010,27(2):1-3.2 最優性條件