基于屬性掌握概率的認知診斷模型

毛秀珍

(四川師范大學 教育科學學院, 四川 成都 610066)

1 預備知識

認知診斷理論是基于項目反應理論的新一代測量理論.它通過分析學生的作答反應獲得學生知識結構中優勢與不足的診斷信息,在教育實踐中發揮著重要作用.一方面,根據認知診斷理論分析的屬性層級關系編制測驗能大大提高測驗的信度和效度；另一方面,根據屬性層級關系分析的學習之路能為選取快速有效的學習方法和教學策略提供指導.因此,認知診斷理論得到了大量的研究與實踐[1-4].一般而言,認知診斷評估包含以下2個步驟.第一,從認知心理學角度分析學生作答項目時采用的知識和技能.第二,根據心理計量學模型擬合測驗反應,據此推論被試的知識狀態和項目特征.由此可見,認知診斷模型是認知診斷研究與應用的基礎.

到目前為止,研究者提出了大量認知診斷模型.D. Bolt[5]將認知診斷方法劃分為4個廣義的類別：潛在類別模型、連續潛在特質模型、基于貝葉斯網絡的認知診斷模型、規則空間方法及其變式:屬性層級方法.特別地,“確定性輸入,噪音‘與’門”模型(DINA)模型和“噪音輸入,確定性‘與’門”模型(NIDA)模型屬于潛在類別模型[6].首先,DINA模型假設測驗要求的屬性之間不具有補償關系,并用猜測和失誤參數模擬作答過程的隨機因素,即si表示當被試掌握項目i考查的所有屬性時錯誤作答項目的概率;表示當被試至少有一個項目i考查的屬性沒有掌握時正確作答項目i的概率.于是,其項目反應函數表示為

P(Xij=1|αj,si,gi)=

(1)

(1)式中αj=(αj1,αj2,…,αjK)為被試j的知識狀態或稱為屬性掌握模式.如果他(她)掌握屬性i,則αji=1,否則αji=0.另外

qik(i=1,2,….N,k=1,2,…,K)為QN×K矩陣的元素,N為測驗包含的項目個數,K等于測驗考查的屬性個數.qik只取1或0,如果項目i考查屬性k,則qik=1,否則qik=0.DINA模型可以區分同一被試在包含相同屬性的不同項目上的反應.然而對每個項目,它只能將所有被試的作答情況分為兩類.當被試掌握項目i考查的所有屬性時ηij=1,其正確作答項目的概率為1-si;如果被試j至少有一個項目i考查的屬性沒有掌握,則其正確作答項目i的概率為gi.因而,DINA模型不能精細地區分不同屬性掌握模式的被試正確作答同一項目的概率,降低了項目的區分度[7].

其次,NIDA模型通過對每一屬性k分別定義猜測參數gk和失誤參數sk,并假設屬性運用滿足局部獨立性,建立項目反應函數如下

P(Xij=1|αj,sk,gk)=

(2)

于是,NIDA模型能區分不同屬性掌握模式的被試對同一項目的作答概率,提高了項目的區分能力.但是,NIDA模型假設項目特征完全決定于其所考察的屬性,忽視了包含相同屬性的不同項目之間的差異[7],從而使得同一被試正確作答包含相同屬性的不同項目的概率相等.

另外,文獻[8]介紹了規則空間方法(RSM).該方法分為特征提取和統計分類2個階段[8].第一階段包括以下5個步驟：首先,領域專家通過分析解題過程中的認知結構形成關于屬性的假設；其次,根據屬性的定義對題目考查的屬性進行編碼,建立屬性與題目之間對應關系的Q矩陣；再次,運用Q矩陣分析鄰接矩陣A、可達矩陣R和理想知識狀態矩陣E；第四,根據矩陣E和Q計算理想作答反應模式；最后,建立規則空間并將理想作答反應和實際作答反應映射為規則空間的點.第二階段借助多元統計或貝葉斯方法實現被試知識狀態的診斷分類.該方法有嚴密的理論基礎,涉及項目反應理論(IRT)和多元統計理論.但它需要多個步驟才能完成對屬性掌握概率的分析,同時每一步的結果都會影響下一步運算和最終結果,從而增加診斷誤差.

鑒于上述常用認知診斷方法的不足,本文將在模型擴展、模型求解和模型效能3個方面做一些探索.

2 屬性掌握概率認知診斷模型的建立和參數估計方法

2.1屬性掌握概率認知診斷模型(AMPM) 本文定義屬性掌握概率為：對考察屬性k的N個項目,假設被試正確作答項目中該屬性部分的項目個數為n,則他正確作答屬性k的頻率為n/N.當項目個數N趨于無限大時,頻率的穩定值定義為屬性k的掌握概率,它在測驗中體現為正確作答屬性k的概率.

假設測驗一共考察K個屬性,則被試j的屬性掌握概率模式表示為K維向量

MPj=(MPj1,MPj2,…,MPjk,…MPjK),

其中MPjk(k=1,2,…,K)取值于[0,1],表示被試j掌握第k個屬性的概率.在Q矩陣前提下,定義失誤參數si表示被試因失誤錯誤作答項目i的概率,即

猜測參數gi為被試因猜測等因素正確作答項目i的概率,即

si和gi不隨被試的不同而發生變化.假設屬性運用滿足局部獨立性,AMPM模型表示為

(3)

該模型綜合了被試的知識結構、項目特征和作答過程等信息擬合項目反應.當屬性掌握概率取1或0時,AMPM和DINA模型一致.與DINA、NIDA和RSM相比,AMPM具有以下幾個優點：1) 它能區別考察相同屬性的不同項目的特征；2) 它能區分不同屬性水平的被試對同一項目的作答概率；3) 屬性掌握概率取值于區間[0,1],能恰當表征應用知識的能力；4) 它以DINA模型為基礎,不增加模型參數的情況下,直接分析屬性掌握概率,為分析被試的知識狀態提供了一種新的視角和方法；5) 參數估計方法簡單,具有實踐可行性.

2.2參數估計

2.2.1方法和工具 馬爾科夫鏈蒙特卡洛(MCMC)算法簡單,不僅能描述具有隨機性質事物的特點,而且收斂速度與問題的維數無關,從而在估計心理計量模型參數中得到了廣泛運用[9-10].于是,本文運用MCMC方法并采用M-H吉布斯算法[9]模擬抽樣,以MATLAB為工具,自編程序進行參數估計.

2.2.2模型參數的先驗分布 文獻[10]在估計模型參數時均假設項目參數服從貝塔分布[11].另外,當樣本量很大時,先驗分布的選擇不會對結果產生很大影響.于是,本文假設項目參數的先驗分布服從4-Beta(γ,η,a,b)分布,即si～4-Beta(γs,ηs,as,bs)和gi～4-Beta(γg,ηg,ag,bg).

借鑒文獻[12-13],本文假設屬性掌握概率向量服從多變量廣義貝塔(MGB)分布.假設X0,X1,…,XΓ是獨立取自伽馬分布的隨機變量,即

Xi～Γ(αi,βi),i=0,1,2,…Γ.

通過變換Y0=X0,

Yi=Xi/(X0+Xi),i=0,1,2,…,Γ,

得到一組隨機變量Y0,Y1,…,YΓ.文獻[12]證明,隨機變量(Y0,Y1,…,YΓ)服從參數為α0,α1,λ1,…,αi,λi,…,αΓ,λΓ的MGB分布,即

(Y0,Y1,…,YΓ)～

其中λi=βi/β0,i=1,2,…,Γ.(Y0,Y1,…,YΓ)的聯合概率密度函數為

0≤yi≤1.

(4)

2.2.3MCMC算法 將各被試參數和項目參數分別組塊,按(MP1,MP2,…,MPJ,s1,g1,s2,g2,…,sI,gI)順序抽取參數.具體地,第t次迭代的MCMC算法如下.

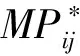
(5)

以及

去的路上，四個人說說笑笑，回來的路上，四個人都有點沉默。之前，只是對未來很茫然，這一刻，卻切切實實全轉化成了壓力。

項目參數的接受概率為

(6)

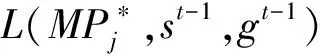
3 模擬研究

模擬研究的目的是驗證MCMC方法估計模型參數的準確性和穩定性.

3.1方法

3.1.1反應數據的產生 首先,根據文獻[4]中20個包含8個屬性的分數減法項目,確定模擬研究的Q矩陣,見表1.其次,根據文獻[10],確定項目參數服從4-Beta(1,2,0,0.25)分布.相應地,產生20組隨機數作為項目參數,見表2中s和g對應的列.

然后,隨機確定MGB(2,7.5,1,5,1,8,1,7,1,5.5,1,6,1,13,1,9,1)作為屬性掌握概率向量的分布,產生1 000個被試的屬性掌握概率向量.

最后,固定Q矩陣、項目參數以及被試參數的分布,一共模擬生成26個數據集.每個數據集包含1 000名被試在考察8個屬性的20個項目上的反應.

3.1.2參數估計 隨機產生均勻分布的隨機數作為模型參數的初始值.每次估計迭代5 000次,采用M-H吉布斯算法模擬抽樣,計算最后3 500次抽樣的平均數作為參數的估計值.

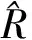
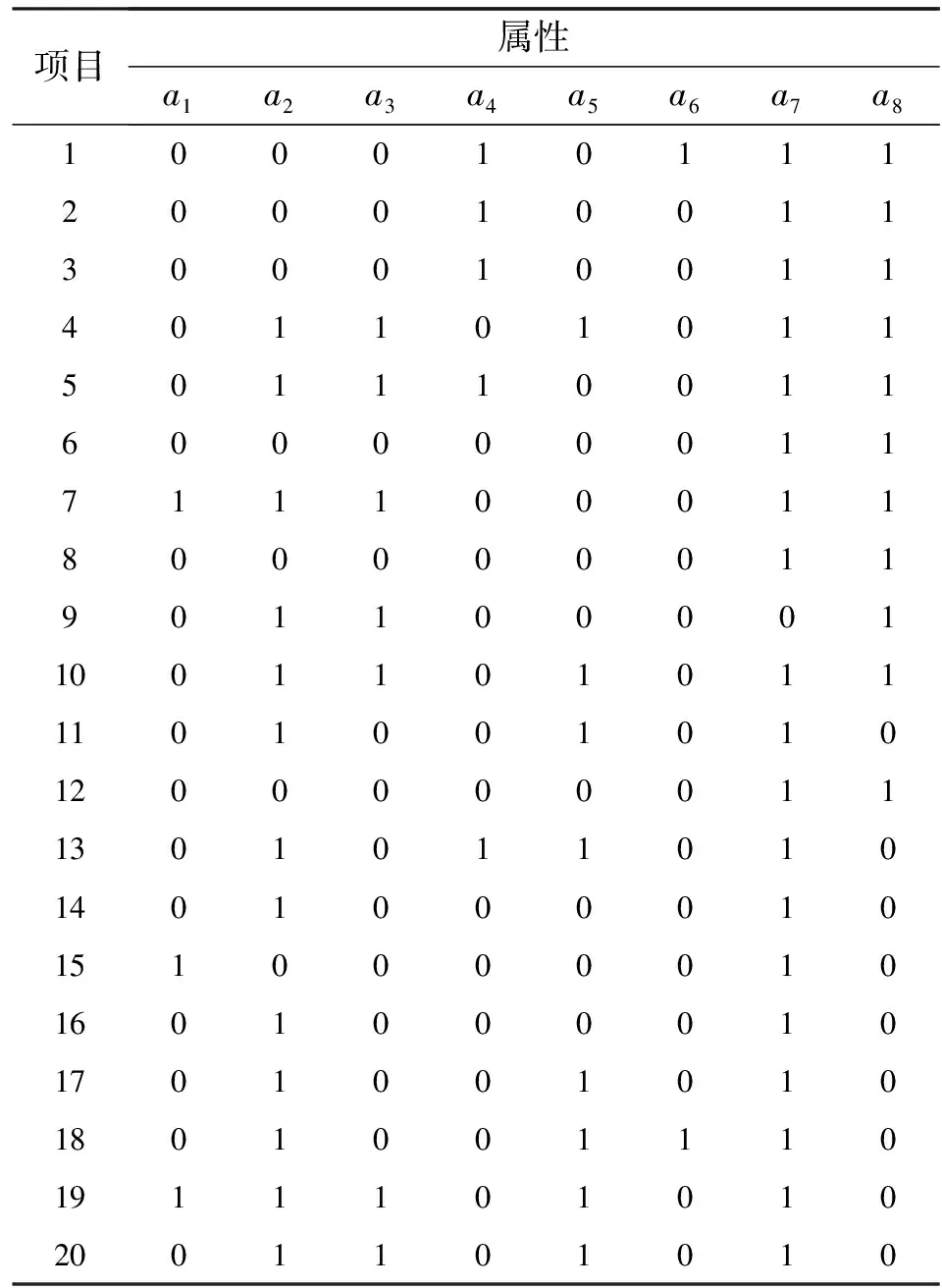
表 1 模擬研究的項目結構Q矩陣

3.2結果

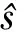
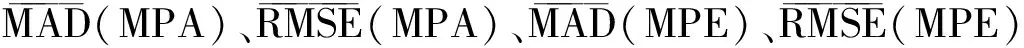
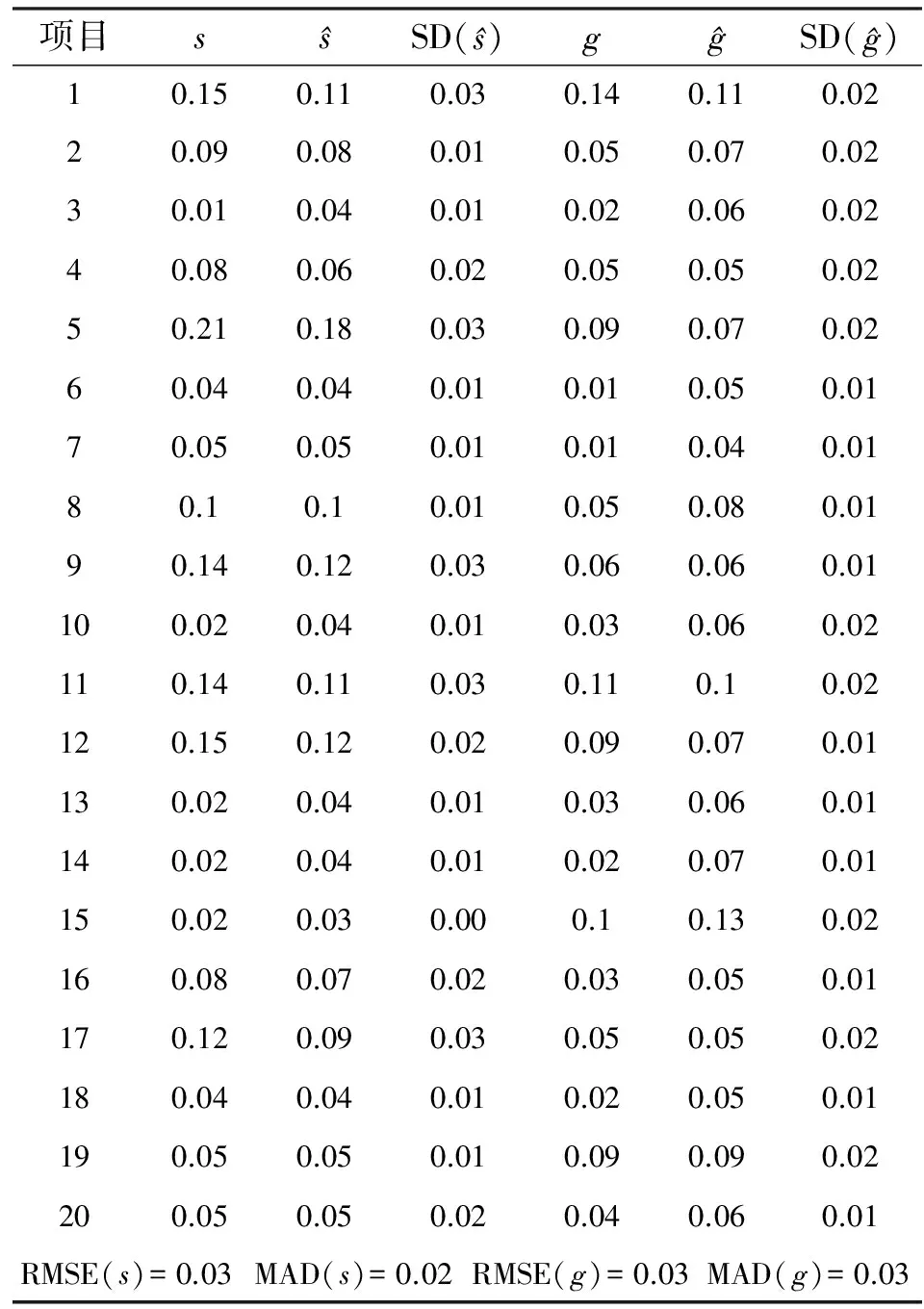
表 2 模擬研究中項目參數的結果

當參數取值于[0,1]且MAD小于0.1時,估計結果較好[15].因此,從表3可知,被試能力估計的準確性和穩定性較好.另外,被試參數中估計最好的是屬性a7,較差的是屬性a6、a2和a5.分析Q矩陣,發現考察屬性a7的項目最多,并且有2個項目只考察屬性a7.考察屬性a6的項目最少,涉及屬性a6的2個項目分別考察了3個和4個屬性,且包含了屬性a2、a5和a4.可見,項目考察的屬性個數和考察每個屬性的項目個數會影響屬性估計的準確性.

4 實證研究

4.1數據描述實證研究采用文獻[16]中40個分數減法項目的反應數據,Q矩陣見表4.他們將40個項目對等地分成2組平行測驗,各有536名學生參加測驗.然后,他們根據A、B的2種解題策略,分別對2組學生的反應做了分析.根據方法B,文獻[16]表明2組中分別有20名和14名學生沒有被分類到任何一個理想屬性掌握模式.因此2個數據集分別包含516名和522名學生的屬性掌握概率.

表 3 模擬研究中被試參數的結果

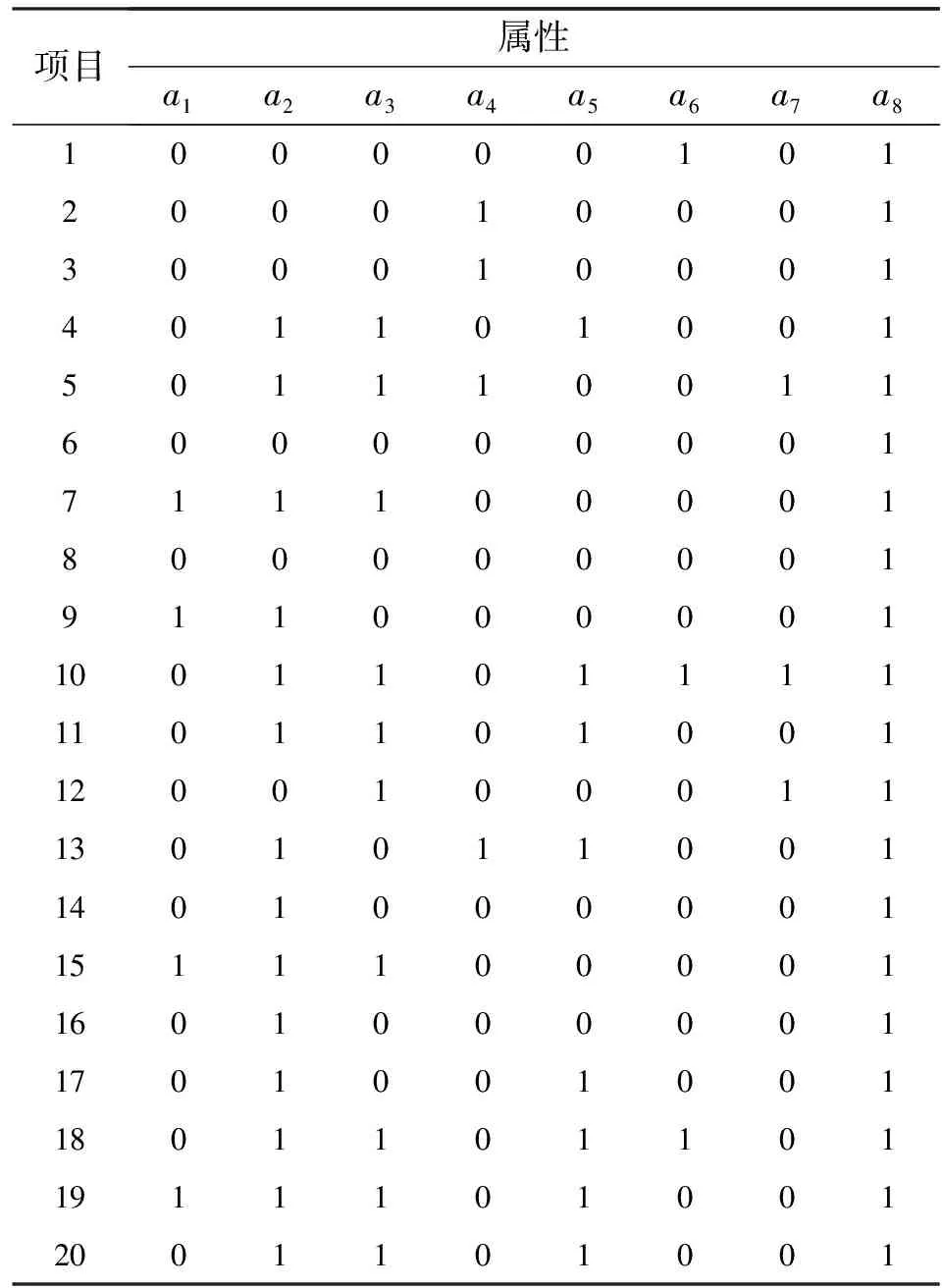
表 4 20個分數減法項目的Q矩陣

本文利用AMPM分析其中516名學生的屬性掌握概率.

4.2參數估計除了屬性掌握概率分布的超參數外,參數估計的方法和步驟與模擬研究一致.根據多變量廣義貝塔分布的特點和數學教師對這8個知識屬性的先驗判斷假設屬性掌握概率的先驗分布為MP～MGB(0.5,0.6,0.9,1.5,1.3,1.1,0.8,0.6,0.2,1,0.7,1.1,0.6,0.9,1.4,1.7).

4.3結果10次獨立估計的項目參數的平均值和標準差,見表5.項目參數取值都小于或等于0.23,模型擬合較好.參數估計與文獻[10]的結果一致.幾乎所有的標準差都小于0.01,結構參數的估計穩定.

對被試參數,采用2個指標考察AMPM與文獻[16]中運用RSM方法所得結果的一致性,見表6.第一,對每個屬性掌握概率,計算AMPM和RSM分析結果的相關系數r.第二,根據AMPM的估計結果,以0.5作為臨界值將被試屬性掌握概率劃分為掌握和未掌握.計算AMPM與RSM在每個屬性上的分類一致比率p,即對所有被試在各個屬性上同時被判斷為掌握和未掌握的人數比率.

實證分析表明,AMPM和RSM有關屬性掌握概率和屬性掌握與否的結果都具有較高的一致性.對每個屬性,屬性掌握概率的相關系數和屬性分類一致比率都大于0.82,其中,屬性a6和a7的分類一致性稍低于其它屬性.根據項目Q矩陣,平均每個項目考察3.25個屬性.分別有3個項目考察屬性a6和a7,并且這些項目都考察了3個以上的屬性.而考察其它屬性的項目都多于3個.可見,項目考察屬性的個數與考察各屬性的項目個數都會影響2種方法分析結果的一致性.這與模擬研究結論一致.

5 結論與討論

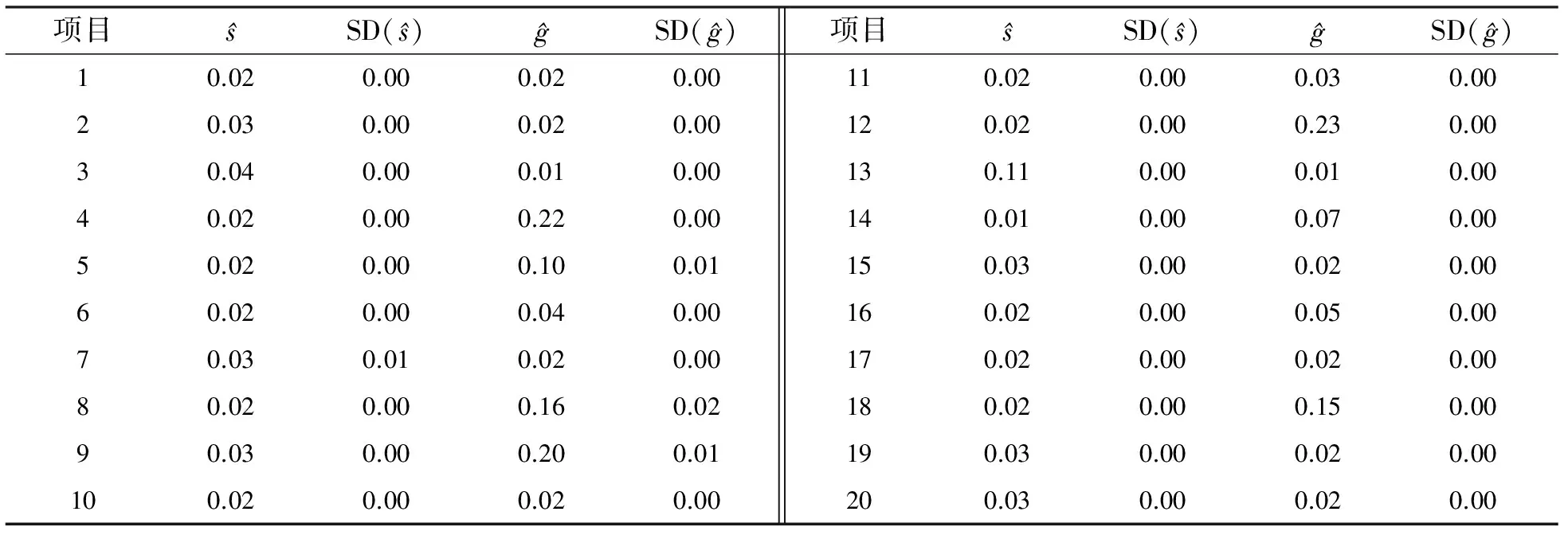
表 5 分數減法數據中項目參數的估計值和標準差

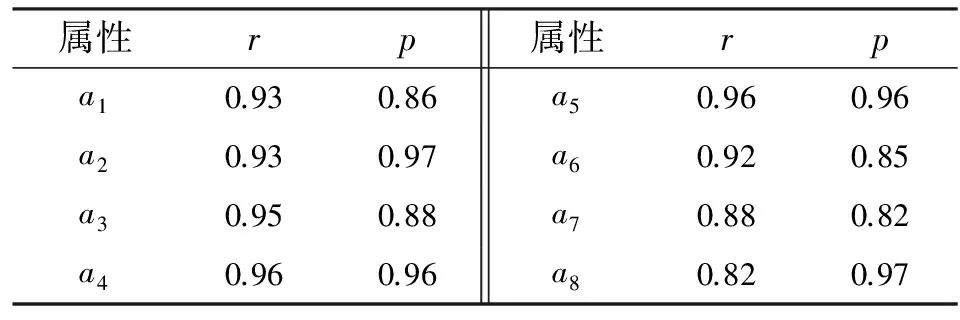
表 6 AMPM和RSM在各屬性上的相關和分類一致性

5.1研究結論已有診斷方法大都假設知識的掌握和應用之間是確定性關系,即一旦掌握某知識,就能正確作答該知識.實際上,掌握一個知識點比正確應用該知識點更容易.正確應用知識與掌握知識的熟練程度相關.因此,本文從分析屬性掌握概率出發,擴展了診斷模型的研究.

首先,基于RSM和DINA模型,建構了屬性掌握概率的認知診斷模型.該模型形式簡潔,符合實際.它不僅能區別考察相同屬性的不同項目的特征,還能區分所有被試對同一項目的作答概率,克服了已有模型的不足.另外,根據屬性掌握概率,依據一定標準還能獲得被試的知識結構.但該模型還存在一些不足之處,例如,作答概率的估計容易受到結構參數的影響；當項目包含的屬性過多時,模型擬合度降低.其次,模擬研究表明,MCMC方法估計項目參數的準確性和穩定性較好.最后,實證研究表明AMPM與RSM的結論比較一致,從而為模型的信度和效度提供了依據.

5.2討論

5.2.1模型比較 認知診斷通過對測驗結構和作答反應的分析,不僅獲得每個學生整體能力的高低,而且能把握他們具備的知識結構和能力水平,并建構知識獲得的最佳途徑.隨著認知診斷理論的興起,以模型為基礎的認知診斷方法層出不窮.診斷模型在追求形式簡潔和高診斷性能的平衡中得到豐富和發展.實際上,模型與數據的擬合程度是選擇與應用模型的關鍵問題.因此,不同模型的比較是今后研究的一個方向.

5.2.2探索多級計分項目的認知診斷模型 目前大部分診斷模型均基于二級計分項目,適用于多級計分項目的認知診斷模型還比較少.實際上,各類型考試均基于多種形式的項目并且大部分屬于多級計分項目.因此,探索適用于多級計分項目的認知診斷模型或在已有模型的基礎上擴展適合多級計分項目的認知診斷模型具有重要意義.

5.2.3認知診斷模型的實踐應用 目前已發展了多種認知診斷方法,國外還開展了廣泛的實踐研究.針對國內壞境,大部分研究都將規則空間方法用于分析實際問題并得到比較滿意的結果.因此,未來研究有必要檢驗其它認知診斷模型的實踐效應.

[1] Embretson S E. A multidimensional latent trait model for measuring learning and change[J]. Psychometrika,1991,56(3):495-515.

[2] Gierl M J, Zheng Y, Cui Y. Using the attribute hierarchy method to identify and interpret cognitive skills that produce group differences[J]. J Educational Measurement,2008,45(1):65-89.

[3] Henson R, Roussos L, Douglas J, et al. Cognitive diagnostic attribute-level discrimination indices[J]. Applied Psychological Measurement,2008,32(4):275-288.

[4] Tatsuoka K K. Cognitive Assessment: an Introduction to the Rule Space Method[M]. New York:Taylor & Francis Group,2009.

[5] Bolt D. The present and future of IRT-based cognitive diagnostic models (ICDMs) and related methods[J]. J Educational Measurement,2007,44(4):377-383.

[6] Junker B W, Sijtsma K. Cognitive assessment models with few assumptions, and connections with nonparametric item response theory[J]. Applied Psychological Measurement,2001,25(3):258-272.

[7] Templin J L, Henson R A, Templin S E. Robustness of hierarchical modeling of skill association in cognitive diagnosis models[J]. Applied Psychological Measurement,2008,32(7):559-574.

[8] 余娜,辛濤. 規則空間模型的簡介與述評[J]. 考試研究,2007(9):14-19.

[9] Patz R J, Junker B W. A straightforward approach to Markov Chain Monte Carlo methods for item response models[J]. J Educational and Behavioral Statistics,1999,24(2):146-178.

[10] de la Torre J, Douglas J. Higher-order latent trait models for cognitive diagnosis[J]. Psychometrika,2004,69(3):333-353.

[11] 張普能,李亮. 多線性分數次積分算子在Herz型Hardy空間中的有界性[J]. 四川師范大學學報:自然科學版,2013,36(5):721-725.

[12] 任靜靜,徐艷艷,陳廣貴. 學習理論中的MLP方法[J]. 四川師范大學學報:自然科學版,2013,36(2):247-251.

[13] Tatsuoka C. Data analytic methods for latent partially ordered classification models[J]. J Royal Statistical Society,2002,C51(3):337-350.

[14] Gleman A, Rubin D B. Inference from iterative simulation using multiple sequences[J]. Statistical Science,1992,7(4) 457-511.

[15] 李峰. 無錨題測驗的鏈接-規則空間模型的途徑[D]. 北京:北京師范大學,2009.

[16] Tatsuoka K K. Architecture of knowledge structures and cognitive diagnosis: a statistical pattern recognition and classification approach[C]//Nichols P D, Chipman S F, Brennan R L. Cognitively Diagnostic Assessment. Hillsdale:Erlbaum,1995:327-359.