時間序列自回歸模型在土壤水分預測中的應用研究

白冬妹，郭滿才，郭忠升，陳亞楠

(1．西北農林科技大學 理學院，陜西 楊凌712100;2．西北農林科技大學 水土保持研究所，陜西 楊凌712100;3．中國科學院/水利部 水土保持研究所，陜西 楊凌712100)

(責任編輯 徐素霞)

黃土高原大部分地區水資源缺乏，土壤水分是限制植被建設的重要因素，一直受到人們的高度關注與重視。土壤水分含量受到很多因素的影響，如氣候條件、土壤、前期土壤水分存儲、土壤水分補給和消耗等［1］，具有很大的隨機性。在黃土丘陵半干旱區，多年生檸條林地土壤旱化嚴重，為了實現土壤水資源可持續利用，需要依據土壤水分狀況，調控檸條生長與土壤水關系［2］，因此監測和預報土壤水分是防旱抗旱、調控檸條生長與土壤水關系的基礎。

時間序列分析主要是采用參數模型對所觀測到的有序隨機數據進行分析和處理的一種方法［3］，這種方法不僅可以分析因果關系，而且能根據時間序列過去的變化規律推斷以后的趨勢［4］。目前時間序列分析廣泛應用于工農業生產、自然科學、社會科學、醫學、金融及各種工程領域［4］。在土壤水分動態模擬方面，劉洪斌等［5］采用時間序列自回歸建模方法對紫色土丘陵旱坡地土壤水分動態進行了模擬和預測，取得了較好的成效;楊紹輝等［3］應用ARIMA 時間序列模型對北京市大興區蘆城的土壤墑情建立模型并預測，認為ARIMA時間序列模型能很好地預測土壤墑情的變化趨勢，有實際的應用價值;張和喜等［6］在干旱地區土壤墑情研究中用到了時間序列自回歸模型，認為該模型可以為干旱研究及治理提供依據。本文在研究黃土丘陵半干旱地區檸條林地土壤含水量動態變化方面運用時間序列自回歸模型，試圖建立合理的模型并預測土壤含水量，為黃土丘陵區植物與土壤水分關系調控和植被建設提供技術支撐。

1 時間序列分析基本原理

1．1 自回歸模型

自回歸模型就是用自身做回歸變量，q 階自回歸過程{Xt}滿足以下方程［7］:

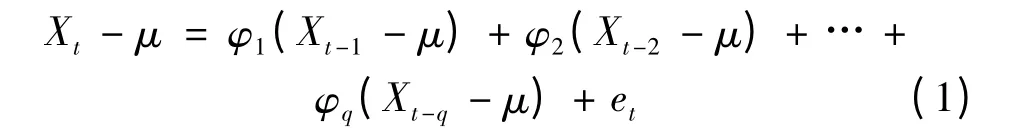
式中:μ 為時間序列的均值;φ1，φ2，…，φq為系數;時間序列{Xt}的當期值是自身最近q 階滯后項和et的線性組合，其中et包括了序列在t 期無法用過去值來解釋的所有新信息。

1．2 相關分析

在時間序列分析中常用自相關系數反映不同時期觀測值之間的相互關系，t 時刻的觀測值與滯后k 時刻的觀測值之間的相關程度稱為時間延遲k 的自相關系數，記為rk，即

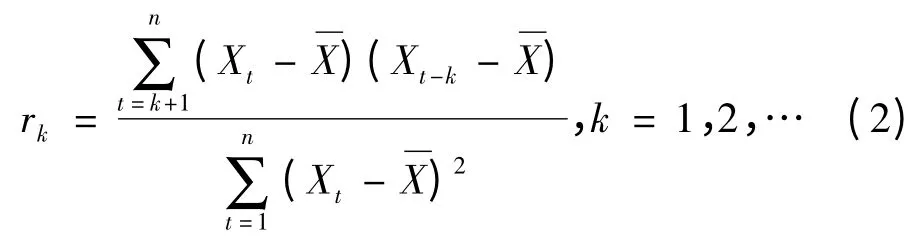
一般情況下計算n/5 個自相關系數［8］，即k =1，2，…，［n/5］。

1．3 定階及模型確定

模型定階的準則主要有自相關函數、偏自相關函數、AIC 和BIC［7］。本文選用研究最多的赤池信息量準則(Akaike’s Information Criterion，AIC)確定自回歸模型的階數，計算公式為

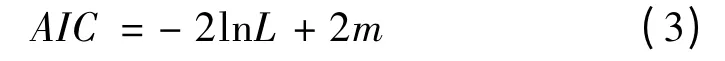
式中:L 為似然函數;m 為參數的數量，如果模型包含截距項或常數項，則m=q+1，否則m=q。

根據土壤含水量時間序列的自相關分析，確定模型的可能最高階，用最大似然估計法估計各階模型的參數，取AIC 最小值對應的階數作為模型的最佳階數，最后確定AR 模型。

1．4 模型診斷

如果模型被正確識別，并且參數估計充分接近真值，那么擬合的殘差應該是獨立同分布的具有零均值和相同標準差的白噪聲序列。擬合模型的適合性檢驗就是檢驗殘差是否是白噪聲序列，文中采用卡方檢驗法驗證白噪聲序列。

設{εt}為選定AR 模型估計出的殘差序列，由式(2)得到殘差序列樣本自相關函數為

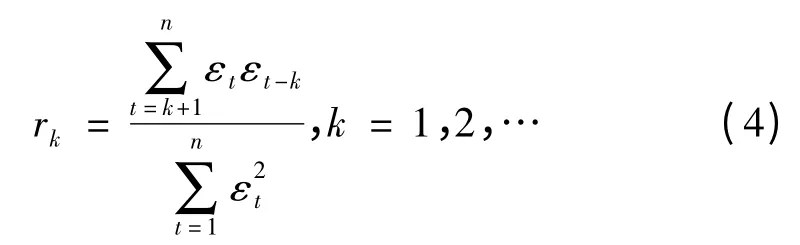
Ljung-Box 統計量［7］計算式為

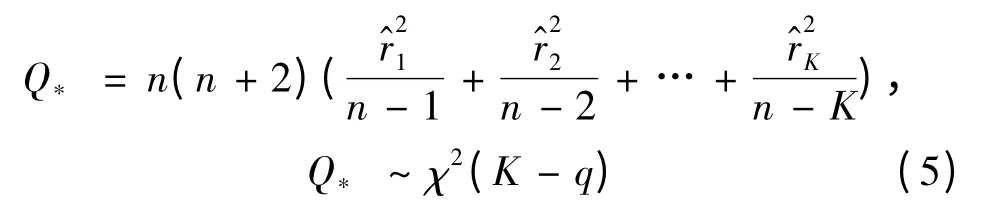
2 研究區概況及土壤水分測定

2．1 試驗區概況

試驗區位于黃土丘陵半干旱區的上黃生態試驗站(寧夏固原)，該站地理位置為北緯35°59'—36°02'、東經106°26'—106°30'。試驗地坡度為0 ～15°，海拔約為1 650 m。該地區年內降水量分配不均，主要集中在6—9月，占年降水量的70%以上，年際降水量變化在634．7(1984年)～259．9 mm(1991年)之間，無霜期152 d，土壤為黃綿土，植被類型為灌叢草原。試驗區主要植物有長芒草(Stipa bungeana Trin．)、阿爾泰狗娃花(Heteropappus altaicus)、茭蒿(Artemisia giraldii Pamp．)、百里香(Thymus mongolicus Ronn．)等。

2．2 土壤水分測定

試驗小區為5 個立地條件基本相同的標準徑流小區，每個小區長20 m、寬5 m，檸條林為2002年播種，各小區播種量分別為2．0、1．5、1．0、0．5、0 kg(對照)。在每個徑流小區中部安置兩個相距2 m 的PVD 套管，管長8 m，用CNC503A(DR)型智能中子水分儀測定土壤水分。測定前對中子儀進行標定，標定方程為y =55．76x+1．89，式中y 為容積含水量，x 為中子儀讀數［10］。土壤水分測定深度為5—780 cm，每20 cm 測定并記錄一次數據。用環刀取樣，測定5 和20 cm 深處土壤水分，對表層土壤水分資料進行驗證和校正。除表層5 cm 測點數值代表0—10 cm 平均值外，其他測點土壤水分值代表測點高度±10 cm 范圍內土壤水分［10］。受當地氣候影響，檸條4月中旬開始生長，10月份之后停止生長，直到第二年4月中旬繼續生長，因此土壤含水量測定時間為:每年4月中旬到10月底每隔15 d 測定一次，11月到次年3月每月測定一次。本文選取2011年4月至2013年2月的土壤水分資料作為研究對象，對檸條林地土壤含水量動態變化進行分析及預測。

3 數據處理及結果分析

3．1 數據預處理

運用MATLAB 及R 軟件處理數據。

3．1．1 數據標準化

通過計算各層土壤含水量的變異系數，發現各土層土壤變異系數存在以下規律:5、20、40 cm 土層土壤水分的變異系數范圍為20% ～30%，屬于比較劇烈的變異;60—120 cm 土層土壤水分的變異系數在10% ～20%之間，屬于中等程度的變異;而140 cm 以下土層土壤水分的變異系數均小于10%，屬于弱變異。這說明表層的土壤水分值變化較快，不穩定，而深層土壤水分值變化緩慢，比較穩定。考慮到各變異程度的土層土壤含水量變化，本研究選取20、80、160 cm 深處土層的土壤水分數據為例進行分析，建立時間序列模型。

為了滿足數據分析的需要，同時提高運算精度，首先應對原始數據進行標準化處理。標準化公式為

式中:Yt為標準化后的時間序列;Xt為原始時間序列;X 是時間序列{Xt}的均值;σ 是時間序列{Xt}的標準差。以20 cm 深處土層土壤含水量序列為例，標準化后如圖1。

3．1．2 平穩性

時間序列模型的分析都是建立在序列平穩的基礎上的，一個平穩的隨機過程有以下要求:均值不隨時間變化;自相關系數只與時間間隔有關，而與所處的時間無關。實際上，自然界大多數時間序列都是不平穩的［11］，由圖1 可以看出，20 cm 深處土層土壤含水量序列是非平穩的。本研究對各土層含水量序列進行了Dickey-Fuller 單位根檢驗，結果見表1。20、80 和160 cm 深處土層的含水量序列經Dickey-Fuller 檢驗后p值依次為0．504 9、0．399 5、0．551 1，均大于0．1，序列存在單位根，所以原始序列為不平穩的。通常經過差分使得序列變得平穩，差分公式為Wt=Yt-Yt-1。經過一階差分之后，檢驗得到的p 值分別為0．035 8、0．014 3、0．051 0，均小于0．1，據此可以認為經過一階差分之后的時間序列為平穩序列。

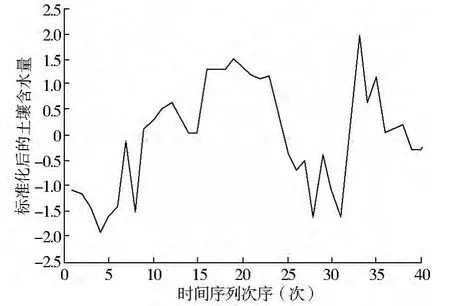
圖1 標準化后的20 cm 深土層土壤含水量序列

表1 各土層含水量時間序列的平穩性檢驗

以20 cm 深處土層土壤含水量為例，差分后序列如圖2，可以看出差分后的序列沒有明顯的時間趨勢;有些時間點上序列波動較劇烈，這是由于20 cm 土層土壤含水量受降雨量影響較大，Dickey-Fuller 檢驗結果認為差分后的20 cm 土層土壤含水量序列為平穩序列，符合時間序列的建模要求。

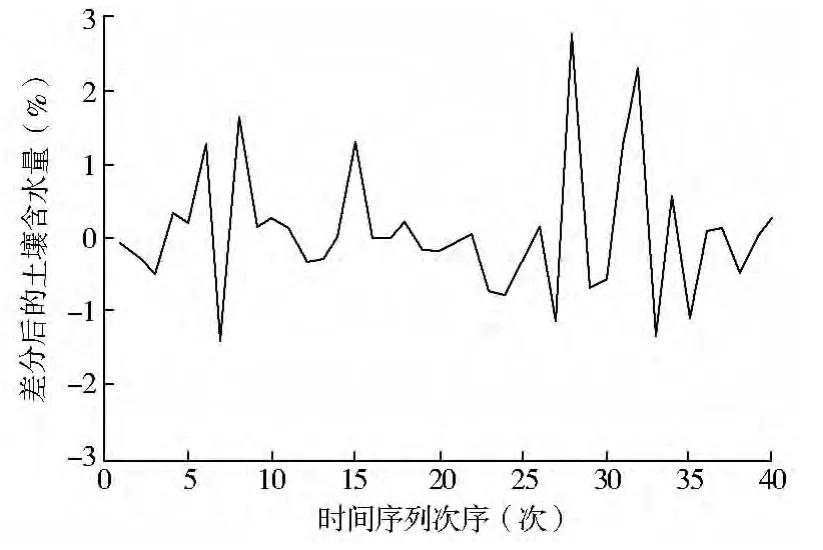
圖2 差分后的20 cm 土層土壤含水量序列

3．2 建立模型

3．2．1 模型的定階及參數估計

應用2011年4月到2012年11月的39 組土壤含水量序列數據進行自相關分析，分析39/5≈8 個自相關系數，結果見表2。rk為滯后階數k 時的自相關系數，當k 值取4 的時候，表2 中20、80、160 cm 三個土層的rk值都比較接近于0，故可以將模型參數估計時的最高階數定為4。

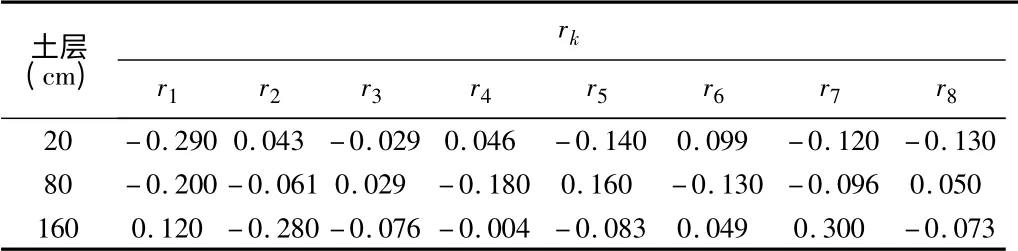
表2 土壤含水量時間序列自相關系數

確定階數后，運用最大似然估計法估計模型的參數，并用式(4)計算各階次的AIC 值，結果見表3。選取AIC 最小值對應的階次為模型的滯后階數，可以看出20 cm 土層AIC 最小值為113．69，說明20 cm 土層含水量序列的模型為AR(1);80 cm 土層AIC 最小值為112．25，確定模型為AR(1);160 cm 土層AIC 最小值為77．35，確定模型為AR(2)。各層土壤含水量擬合模型見表4，Wt為差分后的土壤含水量時間序列。

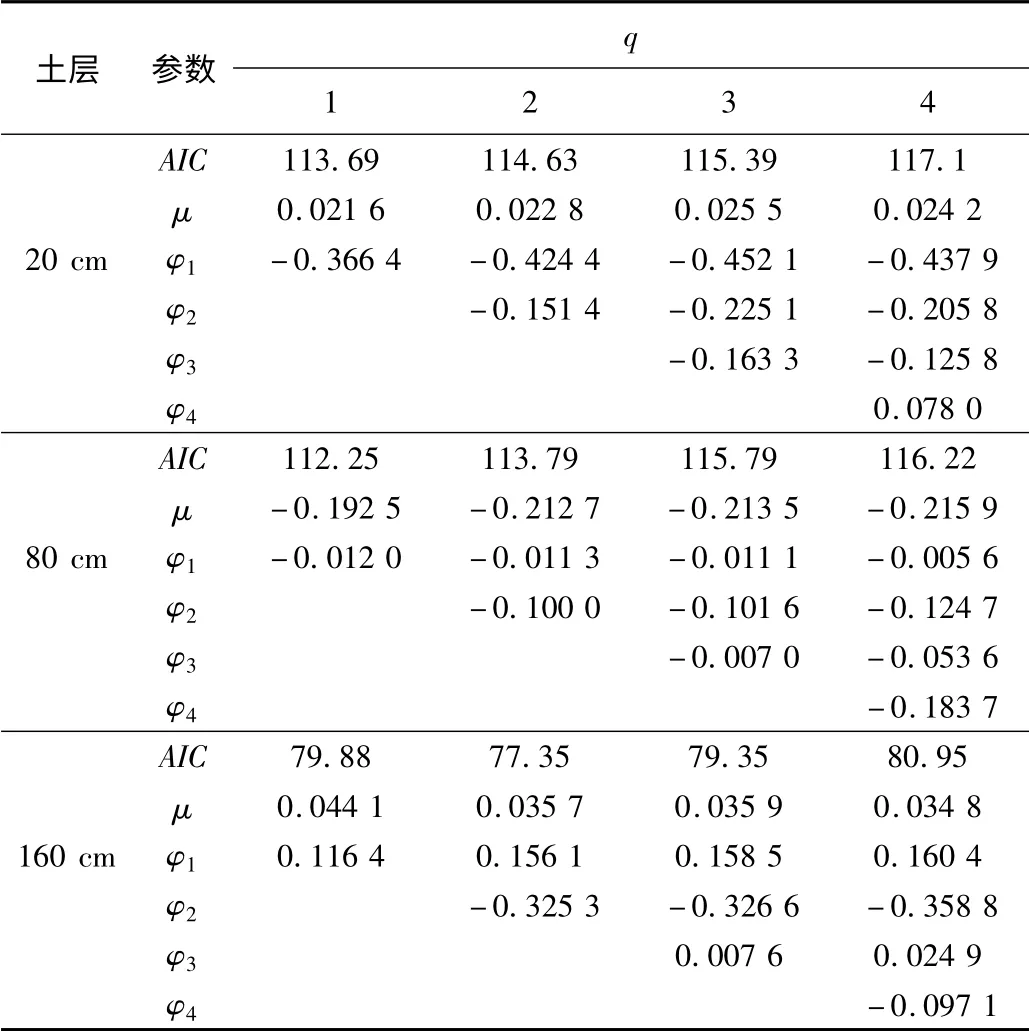
表3 各土層含水量時間序列模型的參數估計結果

表4 各層土壤含水量時間序列模型的擬合結果

3．2．2 模型診斷

由式(1)可知AR 模型的殘差為

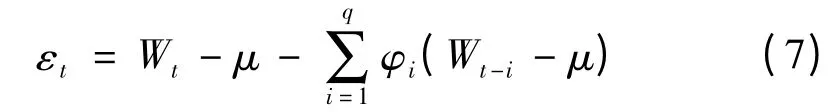
結合式(6)對20、80、160 cm 三個土層土壤含水量序列所對應的模型殘差序列進行白噪聲檢驗，評價模型的擬合優度，模型診斷結果見表5。

表5 各層土壤含水量序列模型的診斷結果

從表5 可以看出，這3 個模型都通過了檢驗，可以認為構建時間序列自回歸模型預測黃土丘陵區半干旱地區檸條林地土壤含水量是合理的。

3．3 模型驗證

一個模型的擬合程度較好不僅在于模型診斷結果，還在于模型的實際驗證。本研究選取2011年4月至2012年11月的39 組數據進行模型擬合，經模型診斷認為擬合較好，為了進一步檢驗模型的實用性，我們運用建立的模型預測2012年12月至2013年2月的6組土壤含水量數據。用Yt-Yt-1替換表4 中的Wt，得到預測模型，將式(6)變為Xt=σYt+X 得到原始時間序列{Xt}，20、80、160 cm 土層土壤含水量實測值與預測值及相對誤差見表6。

由表6 可以看出，未來3 個月的預測數據與實測數據相對誤差較小，20 cm 土層土壤含水量預測值與實測值的相對誤差變化范圍為-5．76% ～5．92%，80 cm 土層實測值與預測值的相對誤差變化范圍為0．05% ～5．28%，160 cm 土層預測值與實測值之間的相對誤差范圍為-5．71% ～2．66%，均小于10%，所以認為本研究建立的自回歸時間序列模型能夠有效地預測土壤含水量，對不同變異程度的土層土壤含水量預測效果也較好，可為黃土丘陵區土壤水分與植物關系調控和植被建設提供技術支撐。

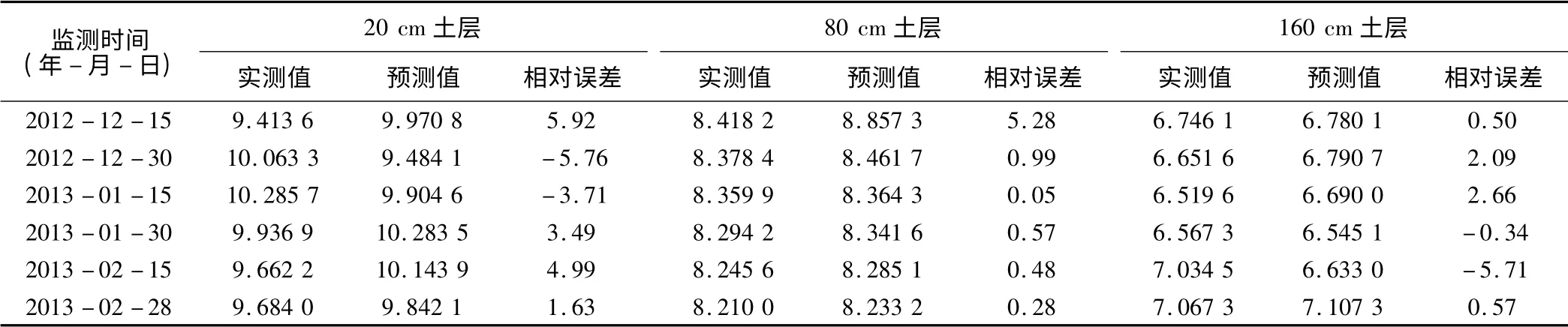
表6 各層土壤含水量序列模型的驗證結果 %

4 結 論

文中將3 個土層土壤含水量序列進行標準化及差分處理后，用Dickey-Fuller 單位根檢驗得出差分后的土壤含水量時間序列為平穩序列，符合時間序列的建模要求。對于時間序列自回歸模型的階數問題，本研究選用AIC 準則確定了3 個土層的階數并建立模型，由卡方檢驗結果認為模型擬合得較好。最后用2012年12月至2013年2月的數據驗證模型，3 個土層預測值與實測值的相對誤差均小于10%，說明該模型對各變異系數的土層土壤含水量預測精度高，更進一步說明了時間序列自回歸模型能夠較好地預測黃土丘陵半干旱地區檸條林地土壤含水量，為該地區植物與土壤水關系的調控及植被建設提供技術支撐。

［1］尚松浩．土壤水分模擬與墑情預報模型研究進展［J］．沈陽農業大學學報，2004，35(5-6):455-458．

［2］郭忠升，李耀林．植物生長與土壤水關系調控起始期［J］．生態學報，2009，29(10):5721-5729．

［3］楊紹輝，王一鳴，郭正琴，等．ARIMA 模型預測土壤墑情研究［J］．干旱地區農業研究，2006，24(2):114-118．

［4］祖元剛，趙則海，于景華，等．非線性生態模型［M］．北京:科學出版社，2004．

［5］劉洪斌，武偉，魏朝富，等．AR 模型在土壤水分動態模擬中的應用［J］．山地學報，2003，22(1):121-125．

［6］張和喜，楊靜，方小宇，等．時間序列分析在土壤墑情預測中的應用研究［J］．水土保持研究，2008，15(4):82-84．

［7］Cryer Jonathan D，Chan Kung-Sik．時間序列分析及應用:R語言［M］．第2 版．潘紅宇，譯．北京:機械工業出版社，2011:1．

［8］秦華光，李家才，穆丹，等．時間序列自回歸模型預測茶園小綠葉蟬種群動態的探討［J］．安徽農業大學學報，2008，35(4):564-570．

［9］于寧莉，易冬云，涂先勤．時間序列中自相關與偏自相關函數分析［J］．數學理論與應用，2007，27(1):54-57．

［10］郭忠升，邵明安．人工檸條林地土壤水分補給和消耗動態變化規律［J］．水土保持學報，2007，21(2):119-123．

［11］李慶雷，馬楠，付遵濤．時間序列非平穩檢測方法的對比分析［J］．北京大學學報:自然科學版，2013，49(2):252-260．