盾構通用管片排版與糾偏控制的簡化解算*

潘國榮 榮一夫

(同濟大學測繪與地理信息學院，上海 200092)

1 引言

通用管片又稱“通用楔形管片”，隧道全部采用楔形管片。通過管片的旋轉組合可以擬合隧道軸線的變化，而使用通用管片的盾構掘進時能通過選擇不同的拼裝點位來擬合設計軸線，因此近年來通用管片的使用越來越受到重視。

本文通過對管片選型的現狀分析，建立了一種結合隧道設計軸線、盾構機軸線、管片成型軸線的簡化管片選型方法，并將該方法用于某地鐵區間的施工過程，結果證明該方法可以有效的提高排版效率并簡化計算過程，同時偏差控制在允許范圍內。

2 通用管片的排版和糾偏

2.1 三軸線簡化解算

將三維空間簡化為平面和垂直兩個獨立的平面，用當前盾構機的姿態，管片姿態和設計軸線數據進行管片選型［1］。管片選型前，需要考慮盾尾間隙、已施工隧道中心線與設計中心線等基本參數，這些參數主要有:管片設計軸線與設計軸線夾角α，α=arctan［(B2－B1)/h］;設計軸線與盾構機軸線夾角β，β=arcsin［(A1－A2)/L］;設計軸線與管片成型軸線的夾角θ，θ=α+β。

在施工中，糾偏情況一般分為三種［2］:偏差小于5 cm、偏差在5 ～10 cm、偏差大于10 cm。本文針對偏差在5 ～10 cm 的情形，在施工中通過設計糾偏線路來擬合設計軸線。

2.2 糾偏線路設計簡化模型

實際施工路線及設計軸線都是在三維的坐標系統中，如果在三維情況下考慮曲線糾偏將加大糾偏難度。本文利用管片成型軸線和隧道設計軸線的夾角進行糾偏曲線的設計，得到一種簡化模型［3］。該簡化方式是將設計軸線簡化為一直線，根據成形管片的夾角趨勢進行線路的設計。然后根據該曲線段是處于直線段，還是緩和曲線段或圓曲線段進行進一步判斷，得到實際的管片超前量和糾偏環數。

該糾偏曲線設計的簡化方法為兩種:一是利用投影曲線將設計軸線拆分為平面線形和縱面線形，獨立考慮糾偏方式，此種方法在施工中得到有效應用;二是通過計算得到的糾偏曲線半徑，可以得到管片的超前量設計值，然后根據該超前量選擇合適的拼裝點位，在排除施工誤差的情況下，可以在較短距離內完成曲線糾偏的任務，保證施工效率［4－6］。

兩種糾偏線路簡化模型為:

1)管片成型軸線和設計軸線成小夾角(0 ＜θ ＜90°)

如圖1 所示，此時盾構機的推進姿態朝向設計軸線，此時只需設計一圓曲線的糾偏曲線對軸線進行糾正，糾偏曲線的終點即為圓曲線的切點，取δ 為設計軸線與管片成型軸線的偏差，即5 cm ＜δ ＜10 cm，L'為糾偏的范圍，由于δ 偏差較小，相對于L'小的多，近似有L'=L，于是可以得到糾偏曲線的半徑為:

以偏差為50 mm 為例，每環糾偏量控制在5 mm/環。則最少需要糾偏環數為10 環，此時糾偏范圍為12 m，通過式(1)可以得到糾偏半徑R=12/2sinarctan(0.05/12)=1 440 m。則平均每環的超前量為

式中r 為管片的環半徑，W 為管片環寬。計算得:Δ=6.2 ×1 200/1 440=5.17 mm。

通過式(2)可以計算出在不同的半徑曲線下，平均每環管片所需的超前量，再根據所需的設計軸線的超前量之和，求出所需的管片組合。同時根據糾偏緩和平穩的原則，每環的糾偏控制在2 ～5 mm，則對于5 ～10 cm 的偏差，其所需的糾偏環數最少為10 ～20 環。

對于小半徑圓曲線設計軸線，應對原有的超前量進行疊加，如本區間的設計曲線半徑為330 m，每環的超前量為Δ=2rW/R=6.2 ×1 200/330=22.7 mm，在偏差為50 mm 的情況下，修正后的超前量為22.7 +5.17=27.87 mm。將設計軸線拆分為直線段，利用弧形糾偏曲線進行擬合，并計算糾偏曲線的長度和所需的每環超前量，然后根據設計的超前量選擇合適的拼裝點位。

2)成型軸線與設計軸線為大夾角(90° ＜θ ＜180°)

根據三軸線關系，糾偏曲線需要設計兩段連續圓弧:第一段是緩和管片成型曲線與設計軸線之間的夾角，使管片成型曲線趨向設計軸線;第二段圓弧類似于1)，即成型軸線通過第一段的糾偏曲線與設計軸線成小夾角，此時通過設計第二段圓弧，使偏向設計軸線的管片成型曲線逐漸緩和過渡，相切于設計軸線，達到糾偏目的。第一段的圓曲線半徑R1可自行設定，但應該大于管片能夠擬合的最小半徑，同時該曲率半徑也要大于盾構機的最小轉彎半徑。圖2 中的夾角θ 計算方法同上。第二段的糾偏方法類似于1)，可計算得到圓曲線的半徑R2。該糾偏曲線的起始于管片成型的當前點，糾偏的終點是與設計軸線相切的某點，該糾偏曲線是一條連續的曲線，是光滑的，所以斜率相同。

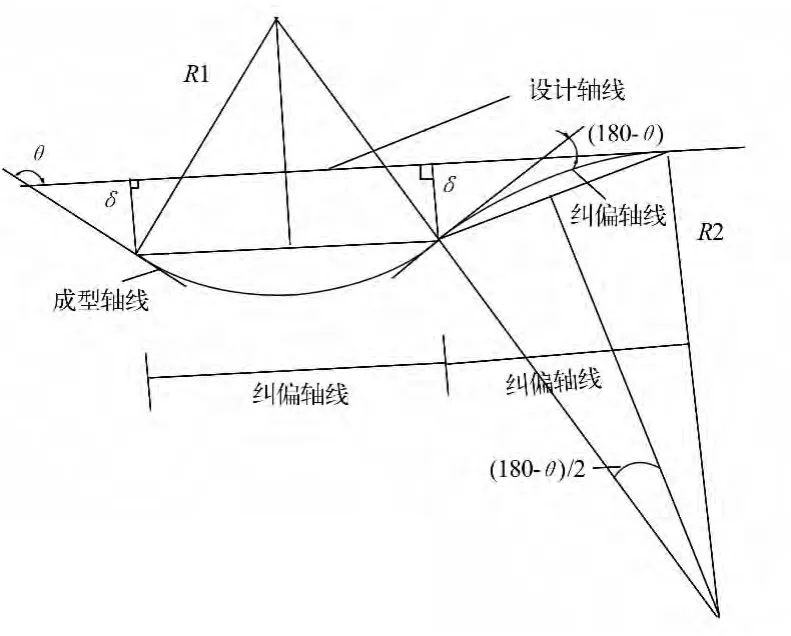
圖2 成型軸線與設計軸線成大夾角Fig.2 Big angle between molding axis and design axis

施工中，管片成型曲線與隧道設計軸線的夾角很小，故此處選取夾角θ 為179°，偏差50 mm，本工程最小曲線半徑為330 m，于是根據需要取第一段糾偏曲線a 的半徑R1為330 m，在第一段糾偏曲線終點處的偏差同取為50 mm，此時管片成型軸線與設計軸線的夾角為1°，計算得到第一段糾偏曲線的弧長為:=11.52 m，對應于環寬為1.2 m 的管片環，需要的管片環數為:11.52/1.2=9.59，取整為10 環。

對于第二段糾偏曲線則計算方式同1)，表1 取第一段糾偏曲線的半徑為330 m，第二段的糾偏曲線的偏差仍為δ，即第一段糾偏曲線和第二段糾偏曲線的偏差相同，便于比較。在實際施工中，應根據此時的偏差重新計算，以得到精確的結果。

表1 成型軸線與設計軸線成大夾角糾偏情況(第一段糾偏半徑為330 m)Tab.1 Correction of the big angle between molding axis and design axis

通過表1 數據可以得到微小的角度變化，也會在糾偏線路中有一定的差異，在設計中必須加入1～2 環的糾偏環，才能保證順利過渡，使管片成型曲線趨向于設計軸線，所以要保證對于角度的精確解算，避免偏差累積造成其他影響。該角度是通過分析盾構機和管片的幾何關系，利用千斤頂行程差、盾尾和切口偏差以及盾構機的參數來進行解算，所以對于這些數據應盡可能地高精度獲取。

方法2)是對糾偏路線進行了簡化。當盾構機偏離設計軸線，即盾構機主體趨勢向外，即可使用該種方式計算，而且只要設計兩段連續的弧形糾偏曲線就可以成功糾正管片成型的偏差。同時，可以根據實際情況進行半徑選取，根據施工情況進行糾偏環數的調整，因此可以減少緩和曲線的應用。

以上兩種簡化方式，基本可以滿足實際施工中發生的情況，當糾偏方向或者起始糾偏位置發生改變時，此方式依然有效。因為是在短距離內緩和平穩的糾偏，施工中可以將設計軸線看成是一直線，通過這種簡化計算，可以根據糾偏的程度選擇不同環數來進行糾偏，以及對糾偏距離做出調整。相對于傳統的窮舉法來進行糾偏設計，本模型適用于短距離的糾偏，不需考慮多種情況，就可以得到有利于施工的糾偏設計，這種簡化方式針對5 ～10 cm 的偏差情況，可以得到很好的結果。但為了保證得到最優的糾偏路線，施工中還應該綜合考慮盾尾間隙、盾構首尾差、油缸行程差等因素。

4 工程分析

以某地鐵區間上行線為例，該區間從里程SK18+422.939 至SK18 +849.420 為一段緩和曲線和圓曲線線路，該段利用上述的方法進行了管片排版和糾偏設計，得到了排版方案，經量測得到偏差結果。

表2 為通過該方式得到的管片排版結果，通過計算糾偏路線和超前量，列出了80 環的管片選型結果，從250 環到330 環，為圓曲線的一段選型排版封頂塊的設計。該設計路線為小半徑圓曲線，相比于窮舉法的五環或者十環糾偏的方法，計算簡便，只需通過計算超前量就可以得到拼裝點位，更有利于實際施工。

表2 250 ～330 環轉彎環的管片排版Tab.2 Segment layout of the turning ring from 250 to 330

統計可得，通過這種設計只要在某些特殊環段改變拼裝點位就可以很好地完成軸線的擬合，而且拼裝方式簡單，基本只在K5、K13、K7 三個拼裝點位進行轉換，并且能保證錯縫拼裝，通縫不超過兩條。通過實際驗證，該方式的偏差都達到了正常狀態的要求，能極大的提高施工效率。

按照該拼裝方式得到的偏差，分別得到了盾構機與設計軸線的偏差結果和管片成型軸線與設計軸線的偏差結果(圖3、4)。

圖3 盾構機與設計軸線偏差Fig.3 Deviation of shield and design axis

圖4 管片成型軸線與設計軸線偏差Fig.4 Deviation of molding segment axis and design axis

圖3、4 顯示，管片成型軸線的偏差絕大多數控制在50 mm 以下，盾構機的姿態偏差也在40 mm 以下，滿足該工程中偏差－100 ～100 mm 的要求。小于50 mm 的姿態一般只需調整盾構機的姿態就可以擬合設計軸線。可見在盾構施工中，通過實時的獲得盾構機推進的千斤頂行程，以及盾構機的姿態差值，判斷盾構機推進軸線、管片成型軸線和設計軸線三者之間的關系，預測管片環的拼裝趨勢，在盾構機出現偏離設計軸線5 ～10 cm 的情況中，可以合理地分析糾偏路線，保證緩和平穩的糾偏推進。這種簡化的計算方式對于管片排版和糾偏有指向作用。

5 結語

通過分析設計軸線、盾構推進軸線、管片成型軸線之間的關系，根據當前管片與軸線的角度情況以及偏差情況，分析得到糾偏路線和長度、糾偏所需的管片超前量，進而得到管片的排版設計。這種方法可以快速地接近設計軸線，計算簡便，可保證施工順利進行。

1 楊群，謝立廣.關于盾構隧道楔形管片環的思考［J］.現代隧道技術，2010，47(3):56－59.(Yang Qun and Xie Liguang.On rings of wedge of shield tunnel segment［J］.Modern Tunnel Technology，2010，47(3):56－59)

2 沈碧輝.盾構通用管片擬合排版技術應用［J］.西部探礦工程，2010(3):177－179.(Shen Bihui.Application of the shield segment fitting typesetting technique［J］.West-China Exploration Engineering，2010，(3):177－179)

3 朱繼文，屠傳豹，賴華輝.通用管片精細化施工研究思路探討［J］.低溫建筑技術，2012，(11):92－94(Zhu Jiwen，Tu Chuanbao and Lai Huahui.Study on the fine construction of general segment［J］.Low Temperature Architecture Technology，2012，(11):92－94)

4 劉鳳華.盾構隧道通用管片擬合排版與管片選型技術研究［D］.同濟大學，2007.(Liu Fenghua.Study on the composition and ring selection technique of general segments for shield driven tunnels［D］.Tongji University，2007)

5 李偉平，鄭國平.盾構隧道通用楔形管片排版系統的核心算法研究［J］.現代隧道技術，2008，(5):34－37.(Li Weiping and Zheng Guoping.Study on core algorithm of the general wedge of shield tunnel segment typesetting system［J］.Modern Tunnel Technology，2008，(5):34－37)

6 劉春，等.長距離隧道盾構管片選型模型與系統實現［J］.大地測量與地球動力學，2008，(6):112－116.(Liu Chun，et al.Rings prediction model in construction of long distance tunnel shield and its computing system［J］.Journal of Geodesy and Geodynamics，2008，(6):112－116)