衛星鐘差超短期預報模型分析*

于合理 郝金明 劉偉平 田英國 張 鶴

1)信息工程大學導航與空天目標工程學院，鄭州 450052

2)96633 部隊，北京100096

1 引言

精密單點定位技術(PPP)由于受制于衛星鐘差產品的實時性和精度，其應用主要停留在事后處理模式上。但實時應用才是PPP 的真正優勢，如何實時獲取高精度的衛星鐘差產品是實現該技術的關鍵［1］。目前，國際地球動力學服務組織(International GNNS Service，IGS)提供的事后精密鐘差產品要延遲12 ～18天才能獲取，即便是超快速精密鐘差也有3 小時的延遲，無法滿足實時精密單點定位的需要。IGS 的預報星歷產品和廣播星歷可以滿足實時要求，但其納秒級的精度不能夠滿足實時要求。

目前美國噴氣推進實驗室(Jet Propulsion Laboratory，JPL)已經能夠以互聯網數據流的形式提供時延幾秒的精密衛星鐘差產品。近幾年我國也開始了廣域實時精密定位原型系統的研究與建設，高精度衛星鐘差的實時獲取是該技術實現的關鍵［2］。但在鐘差獲取過程中，由于數據解算和網絡傳輸都需要一定的時間，解算的精密鐘差產品到達用戶時會產生幾秒至幾十秒的延遲，導致用戶并不能真正實時獲得當前的精密衛星鐘差。因此，對鐘差進行超短期的高精度預報對精密單點定位技術的應用有著非常重要的意義。

雖然已經有大量文獻探討過衛星鐘差的預報［2－7］，但主要都是中長期預報，即使所謂的短期預報也是研究預報一天左右的鐘差，鐘差預報精度一般為幾個到幾十個納秒，而廣域實時精密單點定位系統中所需要的是幾十秒內的超短期預報［2］。因此，目前關于鐘差預報的研究成果還無法直接應用于實時精密單點定位。為此，本文對超短期高精度鐘差預報進行了研究。

2 鐘差預報模型

2.1 二次多項式模型

二次多項式模型為:

其中，Δt=ts－t0，Δtsv為ts時刻衛星鐘差，a0、a1、a2為二次多項式待估參數，t0表示鐘差預報的參考時刻。

當觀測數據多于3 個時，利用最小二乘方法建立模型，求解得到模型參數。考慮到模型求解過程中經常會造成法方程矩陣奇異，進而影響衛星鐘差預報的可靠性和穩定性，本文采用Givens 變換解最小二乘的方法來估計多項式系數［8］，這種解法無需組成法方程，而是直接通過變換觀測方程進行解算，計算效率高且節省內存，在解的精度和數值穩定性都優于通過組法方程的解算方法。

當公式(1)右邊后兩項為零時則變為

2.2 灰色模型

設原始鐘差數據為:

對原始數據x0做一次累加，得對應的新數列為:

其中x1(k)表示一次累加得到新數列x1的第k 個元素，即

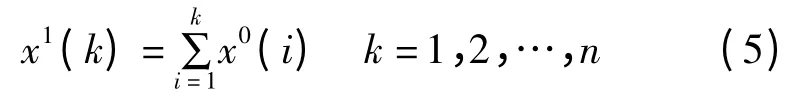
對新生成的數列建立微分方程:

建立關于a 和u 的方程為:

a 和u 根據式(7)利用Givens 變換解最小二乘估計求得。將a 和u 代入微分方程(6)，得

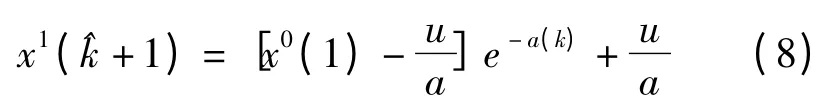
由于x1是x0的一次累加序列，灰色模型預報鐘差可表述為:

2.3 基于歷元間差的二次多項式模型

對原始鐘差數據x0作一次差，得

其中，Δx0(k)，k=1，2，…，n表示歷元k+1 時刻衛星鐘差歷元間差值，

再將歷元間作差得到新數列用二次多項式模型預報后續的鐘差歷元間差，得到鐘差歷元間差數列:

最后再將預報的鐘差歷元間差結果還原為預報鐘差:

3 實驗分析

文獻［9，10］指出，衛星鐘差的預報結果與衛星鐘的類型有很大關系。為使實驗更具代表性和一般性，根據衛星原子鐘類型和衛星編號對照表(表1)，選擇不同類型的1、14、17、25 四顆衛星作為實驗星進行數據分析。

表1 GPS 衛星原子鐘類型和衛星號對照表Tab.1 Atomic clock types of several GPS satellites

研究所采用的試驗數據是歐洲定軌中心(The Center for Orbit Determination in Europe，CODE)發布的2012年1月27日cod05 s 的鐘差，因為本文所討論的是衛星鐘超短期預報，應當先利用拉格朗日方法內插得到每秒一個歷元的鐘差數據。實驗從當天0 時開始，采用前600 s 的數據求解模型參數預報后續300 s 的數據。

32、28、7、1 四顆衛星運用四種方法預報鐘差精度的殘差分析圖如圖1 ～4 所示。縱軸LM、QP、GM、ED 分別表示采用線性模型、二次多項式模式、灰色模型和基于歷元間差的二次多項式模型預報結果事后精密鐘差的殘差曲線。

由圖1 ～4 可知，四種方法對不同類型衛星的鐘差預報精度大致相同。在5 分鐘的預報時間內，32號 衛星誤差為－0.06 ～0.3ns，28號衛星誤差為－0.20 ～0.15 ns，7 號衛星誤差為－0.35 ～0.10 ns，1 號衛星誤差為－0.10 ～0.02 ns。

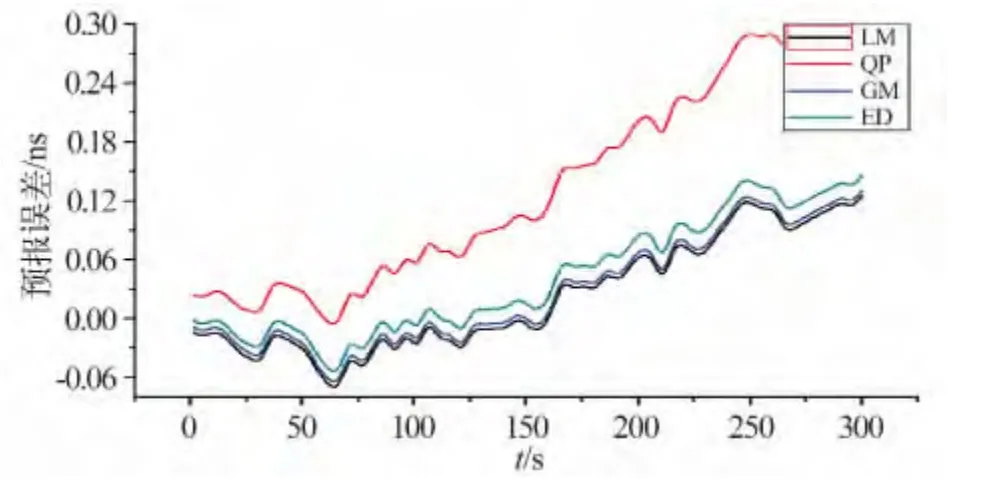
圖1 32 號衛星鐘差預報殘差Fig.1 Residuals of clock error prediction of Sat.32

圖2 28 號衛星鐘差預報殘差Fig.2 Residuals of clock error prediction of Sat.28

采用四種模型預報鐘差的精度基本相當，且誤差殘差變化趨勢基本一致，證明了四種預報方法的正確性。雖然四種預報方法在長期預報中各有局限性，但對超短期預報而言，四種方法都能達到較高的精度水平。四種方法對不同種類衛星5 分鐘的預報精度都能控制在0.36 ns 以內。在更短時間內，衛星鐘差幾秒、幾十秒的預報精度將會更高，能夠滿足實時精密單點定位的需要。

圖3 7 號衛星鐘差預報殘差Fig.3 Residuals of clock error prediction of Sat.7

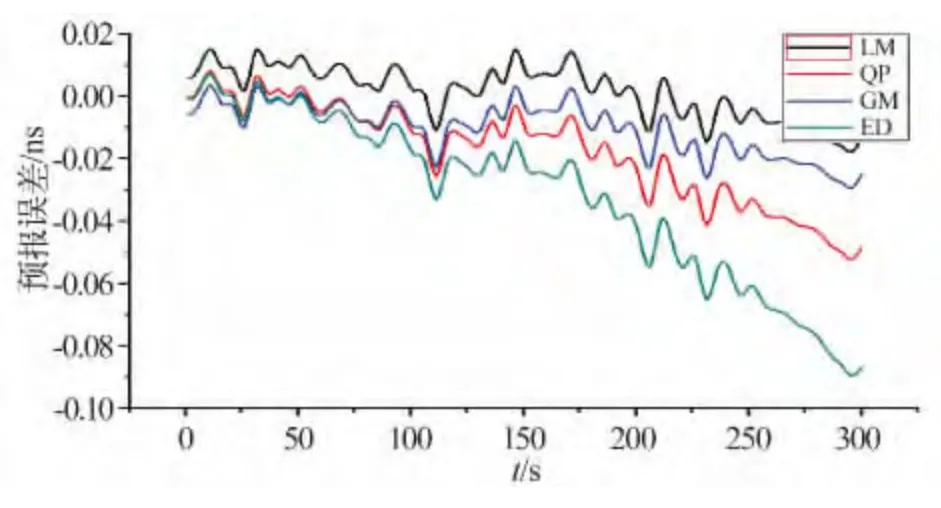
圖4 1 號衛星鐘差預報殘差Fig.4 Residuals of clock error prediction of Sat.1

銣鐘較銫鐘穩定，在衛星鐘差的長期預報或短期預報中一般認為銫鐘的預報精度要低于銣鐘。但對比圖4 和圖1、圖2、圖3 可知，1 號衛星雖為銫鐘但預報精度并不比其他衛星鐘的預報結果差，在這種小樣本的超短期鐘差預報中，預報鐘差精度與衛星和衛星鐘的類型的相關性并不是很大，可能是由于鐘差不同時段內的小尺度變化所引起的。為此本文對同一衛星不同時段的結果進行了分析，以1 號衛星為例，采用同一天數據從第5 個小時開始，取前600 s 的數據求解模型參數預報后續300 s 的數據，預報殘差結果如圖5。

圖5 1 號衛星(5 小時)鐘差預報殘差Fig.5 Residuals of clock error prediction of Sat.1(5 hours)

對比圖4、5 可知，同為1 號星同樣采用600 s 的數據求解模型參數預報后續300 s 的數據，0 時開始預報的殘差為0.1 ns，而5 時開始預報的殘差最大值還不到0.04 ns，因此，同一衛星的預報精度與所選取的時段有重要關系。衛星在某一時段的預報精度主要取決于各衛星鐘鐘差在不同時段內的小尺度變化以及所預報時間的長短。

4 結論

雖然線性模型、二次多項式模型、灰色模型和基于歷元間差的二次多項式模型四種衛星鐘差預報方法在長期預報鐘都存在各自的缺點和局限性，但在超短期預報中精度都很高，都能滿足實時精密單點定位的要求，該文也從側面證明了廣域實時精密單點定位系統的可行性。不同種類的衛星，不同的預報方法的預報精度各有不同，但四種方法在超短期預報中整體上精度相當，其預報誤差變化趨勢也基本一致，并沒有哪種方法明顯優于其他方法。

在這種小樣本的超短期鐘差預報中，預報鐘差精度與衛星和衛星鐘的類型的相關性很小。衛星在某時段的預報精度主要取決于衛星鐘鐘差在該時段內的小尺度變化以及所預報時間的長短。

致謝感謝全球連續監測評估系統( IGMAS)信息工程大學分析中心對本文工作的支持。

1 阮仁桂.GPS 非差相位精密單點定位研究［D］.信息工程大學測繪學院，2009.(Ruan Rengui.Study on GPS precise point positioning using un-differenced carrier phase［D］.Information Engineering University，2009)

2 宋偉偉.導航衛星實時精密鐘差確定及實時精密單點定位理論方法研究［D］.武漢大學，2011.(Song Weiwei.Study on real-time clock offset determination and real-time precise point positioning［D］.WuhanUniversity，2011)

3 劉曉剛，等.幾種時間預報模型的鐘差長期預報效果分析［J］.測繪通報，2011，1:15－17.(Liu Xiaogang，et al.Analysis of long-term clock bias forecast effects of several time prediction model［J］.Bulletin of Surveying and Mapping，2011，1:15－17)

4 王繼剛，等.組合模型預報導航衛星鐘差［J］.大地測量與地球動力學，2012，(1):84－88.(Wang Jigang，et al.Combination models of clock error prediction for navigation satellite［J］.Journal of Geodesy and Geodynamics，2012，(1):84－88)

5 Yuan Haibo，et a1.Dynamic grey-autoregressive model of an atomic clock［J］.Metrologia，2008，(6):1－5.

6 李瑋，等.灰色系統模型在衛星鐘差短期預報中的應用［J］.測繪通報，2009，6:32－35.(Li Wei，et al.Application of grey system model to short-time prediction for satellite clock error［J］.Bulletin of Surveying and Mapping，2008，6:32－35)

7 黃觀文，等.GPS 衛星鐘差的估計與預報研究［J］.大地測量與地球動力學，2009，(6):118－122.(Huang Guanwen，et al.Study on estimation and prediction of GPS satellite clock error［J］.Journal of Geodesy and Geodynamics，2009，(6):118－122)

8 巍子卿.用Givens 變換解最小二乘問題［J］.測繪工程，1996，5(2):1－7.(Wei Ziqing.Solving the least squares problem with Givens transformation［J］.Engineering of Surveying and Mapping，1996，5(2):1－7)

9 王潛心，等.GPS 衛星鐘的特性與預報研究［J］.測繪科學，2010，35(2):36－39.(Wang Qianxin ，et al.Study on GPS satellite clock’s behaviors and prediction［J］.Science of Surveying and Mapping，2010，35(2):36－39)

10 郭海榮.導航衛星原子鐘時頻特性分析理論與方法研究［D］.信息工程大學，2006.(Guo Hairong.Study on the analysis theories and algorithms of the time and frequency characterization for atomic clocks in navigation satellite［D］.Information Engineering University，2006)