雙動力源驅(qū)動下的熱連軋機振動特征＊

凌啟輝， 閆曉強， 張清東， 張義方，2

（1.北京科技大學(xué)機械工程學(xué)院 北京，100083） （2.馬鞍山鋼鐵股份有限公司 馬鞍山，243003）

引 言

連軋機振動在軋制領(lǐng)域一直備受關(guān)注［1］。振動發(fā)生時，不僅導(dǎo)致帶鋼表面和軋輥表面出現(xiàn)振痕，嚴重影響產(chǎn)品表面質(zhì)量和降低軋輥在線使用壽命［2］，而且降低了零件的疲勞壽命，惡化了操作環(huán)境，甚至造成堆鋼、爆輥等事故［3］，威脅軋機的安全生產(chǎn)；同時，也降低了高端產(chǎn)品的開發(fā)和生產(chǎn)產(chǎn)量，給企業(yè)帶來經(jīng)濟損失［4］。連軋機振動研究不僅要求研究者具有較深的理論水平和高精的振動在線監(jiān)測裝置及多功能振動信號分析技術(shù)，而且要求提出的抑振措施在現(xiàn)場能夠容易實現(xiàn)，故使軋機振動研究和抑制變得異常復(fù)雜［5-6］。許多學(xué)者重點研究冷連軋機、平整機組、熱連軋機和中板軋機等出現(xiàn)的振動現(xiàn)象［7-10］，具體研究內(nèi)容為軋機固有動力學(xué)特性、軋機振動傳遞過程、軋機振動現(xiàn)象捕捉、軋機振動產(chǎn)生機理和抑制軋機振動措施等，取得了一些成果［11-13］。

近年來，隨著軋鋼裝備水平不斷提高，熱連軋機呈現(xiàn)出越來越復(fù)雜的多種現(xiàn)象并存的振動，表現(xiàn)為“幽靈”式振動，成為世界范圍內(nèi)軋制領(lǐng)域亟待解決的一個技術(shù)難題。熱連軋機由主傳動系統(tǒng)變頻電機和液壓壓下液壓缸同時對軋機輥系提供工作所需能量，因此，軋制帶鋼時輥系的動力學(xué)特性，應(yīng)同時考慮主傳動系統(tǒng)扭振和液壓壓下系統(tǒng)垂振的影響。

1 現(xiàn)場測試分析

以通鋼熱連軋機振動最為強烈的F3軋機為例，主電機扭矩可用一個恒定扭矩M0和一個波動扭矩Ms之和來表示，電機輸出軸波動扭矩波形及其頻譜如圖1所示，信號采樣時間為0.001s。恒定扭矩為外擾力時，系統(tǒng)最終會趨于穩(wěn)定，因此，只需考慮波動扭矩對振動的影響，可表示為

其中：ω′1為扭矩波動主頻；Ms1為波動扭矩幅值。

液壓缸缸體傳給支承輥軸承座的軋制力可以看成一個恒定軋制力Fs0和一個波動的軋制力Fs的合成，圖2為該機架傳動側(cè)液壓缸無桿腔波動壓力的時域波形及頻譜圖，采樣時間為0.003s。同理，波動軋制力可表示為

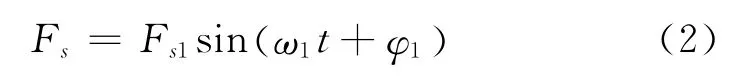
其中：ω1為軋制力波動主頻；Fs1為波動幅值；φ1為扭矩波動量和軋制力波動量之間的相位角。

圖2 波動軋制力波形及頻譜圖Fig.2 Fluctuation rolling force waveform and frequency spectrum diagram

實測工作輥軸承座水平和垂直振動信號如圖3所示，圖3（a，b）分別為工作輥水平方向振動波形及其頻譜，圖3（c，d）分別為工作輥垂直方向振動波形及其頻譜。從圖中可以看出，在軋制薄板時，水平振動比垂直振動更明顯，軋輥水平、垂直方向振動出現(xiàn)了42.75Hz的主頻及不明顯的倍頻，說明此時系統(tǒng)伴有主共振等組合共振現(xiàn)象發(fā)生。

由圖1～圖3發(fā)現(xiàn)，工作輥軸承座振動加速度信號、軋制力信號和電機扭矩信號有相近的主頻，表明在實測信號中發(fā)現(xiàn)了扭振和垂振的耦合現(xiàn)象，熱連軋機振動受雙動力源驅(qū)動的影響。

2 工作輥動力學(xué)模型

以F3軋機上工作輥及軸承座為研究對象，同時受到附加力（扭振通過傾斜萬向接軸傳遞到工作輥上）、軋制力和摩擦力作用，其力學(xué)模型如圖4所示。其中：O1，O2為工作輥支承輥圓心初始位置；kwr1，kwr2分別為帶鋼和工作輥之間在水平方向和垂直方向的等效剛度；cwr1，cwr2分別為帶鋼和工作輥之間在水平方向和垂直方向的等效阻尼；kwr3為工作輥和支承輥之間的等效剛度；cwr3為工作輥和支承輥之間的等效阻尼；khar為牌坊立柱橫向剛度；FS為液壓壓下系統(tǒng)通過上支承輥給工作輥的軋制力波動；FωS為萬向接軸對工作輥的附加水平力；FωV為萬向軸對工作輥的附加垂直力；Fc為工作輥軸承座與牌坊立柱間的摩擦力；FfS為軋制界面摩擦在水平方向的分量；ω0為工作輥轉(zhuǎn)頻；ΔX為工作輥軸承座與牌坊立柱襯板間隙；e為軋機輥系偏移距；θ0為支承輥圓心與工作輥圓心垂直方向存在的初始夾角；θ為支承輥圓心在工作輥圓心垂直方向存在的夾角；d為圓心O1，O2之間的距離；x為工作輥水平振動位移；y為工作輥垂直振動位移。

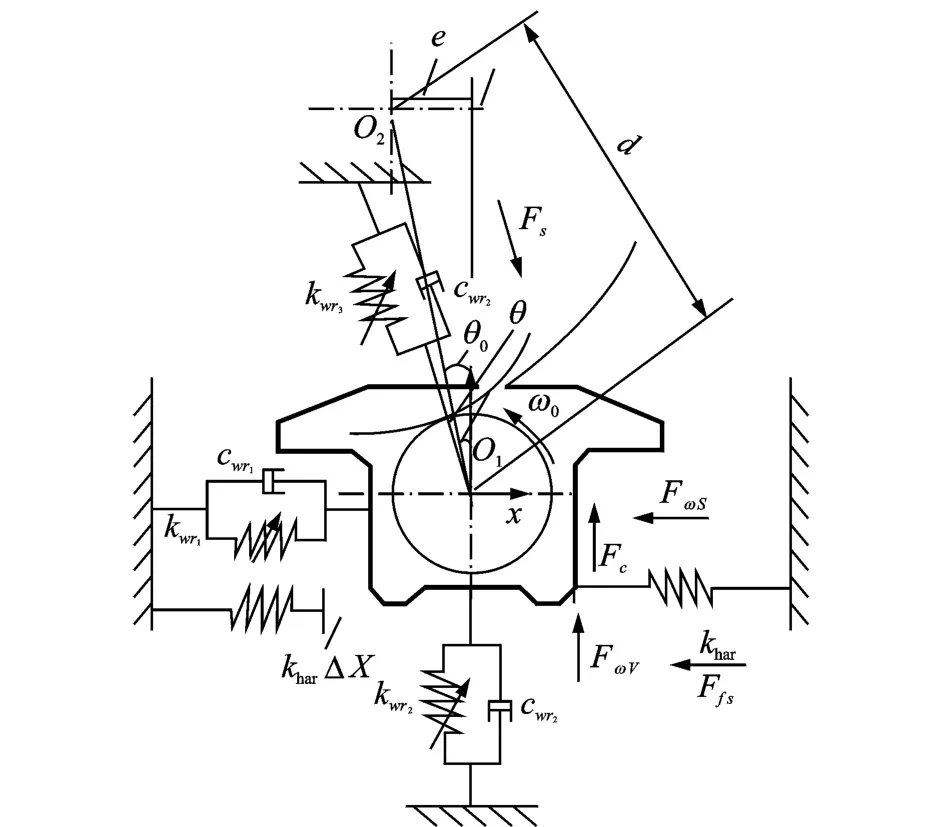
圖4 上工作輥非線性動力學(xué)模型Fig.4 Up work roll nonlinear dynamics model

附加水平力和附加垂直力可參閱文獻［14］來求解。

工作輥軸承座和牌坊立柱間存在間隙ΔX，水平方向的剛度和阻尼是分段的，有力函數(shù)f（x）

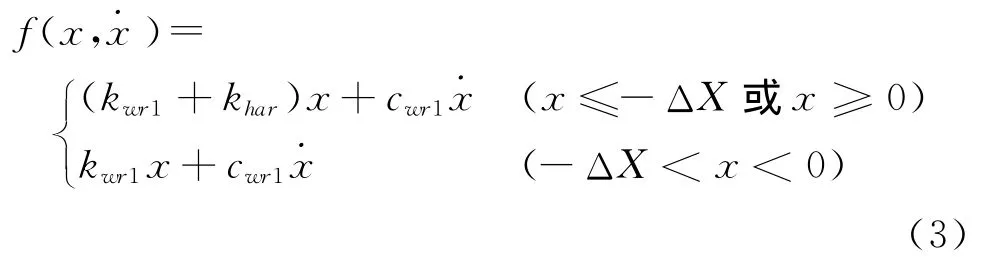
工作輥軸承座與牌坊立柱之間產(chǎn)生的摩擦力Fc屬干摩擦潤滑［15］，其大小與接觸壓力和摩擦系數(shù)μ1有關(guān)，有

其中：μ1為工作輥軸承座與牌坊立柱之間的干摩擦因數(shù)（取0.2）；FNc為工作輥軸承座與牌坊立柱之間的正壓力。

這里只考慮軋制力和扭矩的波動對振動的影響，認為軋輥與帶鋼之間的動摩擦因數(shù)μ完全服從庫倫阻力定律時，即動摩擦因數(shù)與軋制速度的大小無關(guān)，摩擦力只與帶鋼和軋輥之間的正壓力有關(guān)［16-17］。軋制界面水平方向摩擦力僅與軋制力波動量有關(guān)，動摩擦因數(shù)取0.1，有

由工作輥動力學(xué)模型，建立振動微分方程如下。

水平方向

垂直方向

其中：m為上工作輥及其軸承座的集中質(zhì)量。

運用數(shù)學(xué)幾何的知識可求得支承輥圓心在工作輥圓心垂直方向的偏角θ與振動位移x，y的關(guān)系

軋鋼時，主電機和液壓壓下系統(tǒng)同時給軋機輥系提供動力，屬于雙動力源驅(qū)動，從振動微分方程可看出，雙動力源對工作輥提供了振動所需的能量，存在垂直振動和水平振動的耦合。

3 仿真研究

3.1 動態(tài)響應(yīng)研究

根據(jù)上面建立的振動微分方程，取軋制力波動幅值Fs1＝4.5×105N，電機扭矩波動量幅值Ms1＝1.268×105N·m，分別代入式（1）和式（2），按照軋機參數(shù)計算出其他參數(shù)，用Matlab編程并進行數(shù)值仿真求解［18］。圖5相圖為閉合軌跡，說明系統(tǒng)運動是周期的。圖6為龐加萊（Poincare）截面圖，此時龐加萊截面圖為少數(shù)零散的幾個點，未出現(xiàn)擬周期吸引子和混沌吸引子，說明系統(tǒng)運動是周期的。

圖5 系統(tǒng)響應(yīng)的相圖Fig.5 Phase diagram of system response

圖6 龐加萊截面圖Fig.6 Poincare diagram

對系統(tǒng)速度響應(yīng)進行求導(dǎo)可得系統(tǒng)的加速度響應(yīng)。圖7（a，c）為加速度響應(yīng)時域波形，可以看出水平方向振動較垂直方向振動厲害，隨著時間的變化，水平加速度響應(yīng)和垂直加速度響應(yīng)振幅基本保持不變。對加速度時域信號作傅里葉變換可得加速度頻域波形。圖7（b，d）為加速度響應(yīng)對應(yīng)的頻譜，水平方向和垂直方向主要以主頻振動，倍頻不明顯，這與實測工作輥軸承座振動信號、軋制力和主電機輸出扭矩主頻相吻合，說明了雙動力源對輥系振動的影響。

圖7 加速度響應(yīng)波形圖及其頻譜圖Fig.7 Acceleration response waveform diagram and spectrum diagram

改變扭矩波動量和軋制力波動量之間的相位角時，上工作輥水平振動與垂直振動大小對比如圖8所示，相位角每20°計算1次。從圖中可看出，當扭矩波動量和軋制力波動量之間的相位角為180°左右時水平振動最弱，當相位角為200°左右時垂直振動最弱，說明改變扭矩波動量和軋制力波動量間相位角能緩解振動。

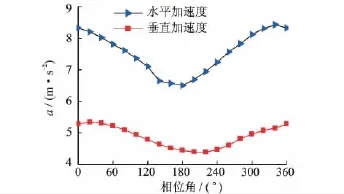
圖8 振動強度隨扭振和垂振之間相位角的變化Fig.8 Vibration intensity with torsional vibration and vertical vibration phase angle changed

3.2 系統(tǒng)分岔特性研究

為進一步研究電機扭矩和軋制力對輥系振動的影響，分別以軋制力波動量幅值和扭矩波動量幅值為分岔參數(shù)的振幅分岔圖［19］來描述輥系振動特性。繪制以扭矩波動量幅值為分岔參數(shù)的振幅局部分岔圖如圖9所示，可以看出，系統(tǒng)隨著扭矩激勵的增大表現(xiàn)出復(fù)雜的分岔現(xiàn)象，水平方向位移響應(yīng)的分岔行為較垂直方向位移響應(yīng)的分岔行為明顯。繪制以軋制力波動量幅值為分岔參數(shù)的振幅分岔圖如圖10所示，隨著軋制力波動幅值的增加，在軋制力波動幅值達到1.5×105N時水平方向位移響應(yīng)由周期1分岔進入周期2的運動；在軋制力波動量幅值達到2.05×105N時，水平方向位移響應(yīng)進入混沌運動；在軋制力波動量幅值達到2.6×105N時，發(fā)生周期1運動離開混沌區(qū)，而垂直方向位移響應(yīng)一直以周期1運動。由圖9和圖10可以看出，電機扭矩、軋制力波動量幅值主要影響水平方向振動。

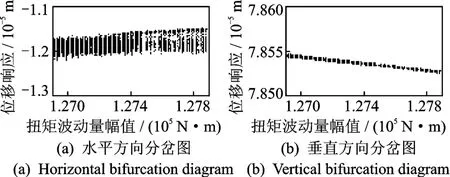
圖9 扭矩波動量為分岔參數(shù)的局部分岔圖Fig.9 The part of the bifurcation diagram，bifurcation parameter with torque fluctuation

圖10 軋制力波動量為分岔參數(shù)的分岔圖Fig.10 The bifurcation diagram，bifurcation parameter with rolling force fluctuation

4 結(jié) 論

1）在軋制過程中，主傳動系統(tǒng)扭振和液壓壓下系統(tǒng)垂振同時作用于軋機系統(tǒng)，兩者能分別并相互影響軋機系統(tǒng)工作輥水平振動和垂直振動，軋機振動屬雙動力源耦合振動。

2）改變扭矩波動量和軋制力波動量之間的相位角可影響輥系振動強度，當相位角為180°左右時水平振動最弱，相位角為200°左右時垂直振動最弱。因此，可通過控制軋制力波動量與扭矩波動量之間的相位差來緩解軋機振動，提出了一條抑制軋機振動的新思路。

3）軋制力、電機扭矩波動量幅值的變化會導(dǎo)致工作輥位移響應(yīng)發(fā)生分岔和混沌等行為，體現(xiàn)了輥系在軋制過程中的非平穩(wěn)特征。

4）對仿真與現(xiàn)場測試進行對比，其結(jié)果驗證了熱連軋機雙動力源驅(qū)動下工作輥分段非線性動力學(xué)模型的正確性。

［1］ Eugenio B，Luca L.Numerical and experimental analysis of the dynamic effects in compact cluster mills for cold rolling［J］.Journal of Materials Processing Technology，2009，209（5）：2436－2445.

［2］ Paul A，Han W.Modeling and simulation of vibration phenomena in rolling mills［C］∥ 7th International Steel Rolling Conference.Japan：Chiba，1998：166－171.

［3］ Hu P.Stability and chatter in rolling ［D］.Evanston：Northwestern University，1998.

［4］ Efrain U.Identification and countermeasures to resolve hot strip mill chatter［J］.AISE Steel Technology，2001，78（6）：48－52.

［5］ 閆曉強，史燦，曹曦，等.CSP軋機扭振與垂振耦合研究［J］.振動、測試與診斷，2008，28（4）：377－381.

Yan Xiaoqiang，Shi Chan，Cao Xi，et al.Research on CSP rolling mill coupling of torsional vibration and vertical vibration［J］.Journal of Vibration，Measurement ＆ Diagnosis，2008，28（4）：377－381.（in Chinese）

［6］ 閆曉強，崔秀波.基于NRF9E5的軋機扭矩遙測系統(tǒng)［J］.微計算機信息，2007，23（25）：113－114.

Yan Xiaoqiang，Cui Xiubo.Torque telemetering system of main drive system for rolling mill based on NRF9E5［J］.Microcomputer Information，2007，23（25）：113－114.（in Chinese）

［7］ Hu Peihua，Zhao Huyue，Ehmann K F.Third－octavemode chatter in rolling，part 1：chatter model［J］.Proceedings of the Institution of Mechanical Engineers，Part B：Journal of Engineering Manufacture，2006，220：1267－1277.

［8］ 楊旭，李江昀，童朝南.冷軋機傳動系統(tǒng)振動測試與控制策略［J］.振動、測試與診斷，2013，33（1）：99－105.

Yang Xu，Li Jiangyun，Tong Chaonan.Cold rolling mill drive system vibration test and control strategy［J］.Journal of Vibration，Measurement ＆ Diagnosis，2013，33（1）：99－105.（in Chinese）

［9］ Mashayekhi M，Torabian N，Poursina M.Continuum damage mechanics analysis of strip tearing in a tandem cold rolling process［J］.Simulation Modeling Practice and Theory，2011，19（2）：612－625.

［10］趙麗娟，徐濤，劉杰.基于ADAMS／Vibration的軋機垂直振動模型的研究［J］.系統(tǒng)仿真學(xué)報，2006，18（6）：1566－1569.

Zhao Lijuan，Xu Tao，Liu Jie.Modeling and analysis on vertical vibration of mill using ADAMS／Vibration［J］.Journal of System Simulation，2006，18（6）：1566－1569.（in Chinese）

［11］Bontcheva N，Petzov G.Total simulation model of the thermo－mechanical process in shape rolling of steel rods ［J］.Computational Materials Science，2005，34（4）：377－388.

［12］馬維金，李鳳蘭，熊詩波，等.熱連軋機自激振動診斷與振動機理分析［J］.振動、測試與診斷，2006，26（4）：261－264.

Ma Weijin，Li Fenglan，Xiong Shibo，et al.Analysis and diagnosis of self－excitation－vibration of hot rolling mill［J］.Journal of Vibration，Measurement ＆ Diagnosis，2006，26（4）：261－264.（in Chinese）

［13］鐘掘，唐華平.高速軋機若干振動問題——復(fù)雜機電系統(tǒng)耦合動力學(xué)研究［J］.振動、測試與診斷，2002，22（1）：1－8.

Zhong Jue，Tang Huaping.Vibration problems of high speed rolling mill—study of dynamics of complex electromechanically coupled system［J］.Journal of Vibration，Measurement ＆ Diagnosis，2002，22（1）：1－8.（in Chinese）

［14］閆曉強.四輥中板軋機鋼板波浪生成與抑制之五——工作輥附加水平力的確定［J］.北京科技大學(xué)學(xué)報，1999，21（3）：288－291.

Yan Xiaoqiang.Forming and curbing of jobbing sheet waviness on four high jobbing sheet mill（5）—Setting up the model of additional horizontal force［J］.Journal of University of Science and Technology Beijing，1999，21（3）：288－291.（in Chinese）

［15］王永濤.CSP軋機軋輥振紋對振動的強化機理研究［D］.北京：北京科技大學(xué)，2007.

［16］張瑞成，陳至坤，王福斌.單輥驅(qū)動軋機水平非線性參激振動機理研究［J］.振動與沖擊，2010，29（6）：112－115.

Zhang Ruicheng，Chen Zhikun，Wang Fubin.Research on param ethically excited horizontal nonlinear vibration in single－roll driving mill system［J］.Journal of Vibration and Shock，2010，29（6）：112－115.（in Chinese）［17］Thomsen J J，F(xiàn)id L A.Analytical approximations for stick slip vibration amplitudes［J］.International Journal of Non－Linear Mechanics，2003，38：389－403.

［18］周品.MATLAB數(shù)學(xué)計算與仿真應(yīng)用［M］.北京：電子工業(yè)出版社，2013：194－268.

［19］顧致平.非線性振動 ［M］.北京：中國電力出版社，2012：212－256.