數列在日常理財生活中的應用

趙曼淇

（北京海淀區中央民族大學附屬中學，北京 100081）

一、在銀行理財品種中，數列的應用及數學模型的建立

1.等差數列在零存整取（整存零取）中的應用

什么是零存整取？在銀行存款理財中，有一種零存整取的儲蓄項目，它是每月某日間隔一定時間存入一筆相同的金額，這是零存；到一定時間段后，可以取出全部本金及利息，這是整取。

舉例：我們若從年初開始，每3個月初存入1 000元，3個月零存整取利率為a‰，到第12月底的本息和是多少？

分析：若每3個月初存入1 000元，12個月一共存入4期，合計本金4 000元。我們分別計算每期到12月底的本息和：

第一次存1 000元，到12月底的本息和：A1=本金+利息=1 000+1 000×4×a‰；第二次存1 000元，到12月底的本息和：A2=本金+利息=1 000 +1 000×3×a‰；第三次存1 000元，到12月底的本息和：A3=本金+利息=1 000+1 000×2×a‰；第四次存1 000元，到12月底的本息和：A4=本金+利息=1 000+1 000×1×a‰。

通過觀察不難發現A1、A2、A3、A4構成一個等差數列，公差是1 000a‰，計算到12月份本息和，就是數列A1、A2、A3、A4的四項和，其本息和是：A=1 000×4+1 000×（4+3+2+1）×a‰=4 000+1 000× 10×a‰；我們按照等差數列求和公式，求得本息和A=1 000×4+1 000×［4×（4+1）×（1/2）］×a‰=4 000+1 000×10×a‰。我們可以比較一下，發現兩次計算結果完全相同。

依據以上分析計算，我們得出零存整取或整存零取（單利計息）的存款儲蓄品種，它的本息計算可以按照等差數列求和公式，構建起零存整取（整存零取）的本息和的數學計算模型是：本息和=每期存入金額×［存期數+存期數×（存期數+1）×（1/2）×利率］。（以下記做公式1。）

2.等比數列，在銀行存款中定期轉存的應用

什么是定期轉存？在銀行存款理財中，有一種儲蓄項目，它是從某日存入一定金額的固定存期儲蓄，并約定每次到期存款均自動轉為下一個存期的定期存款，這就是定期轉存。

舉例：我們若從年初開始存入1 000元的3個月定期轉存儲蓄，3個月利率為a‰，到第12月底的本息和是多少？

分析：年初存入的1 000元，3個月到期后，自動轉存時，第一個存期的利息，加入的1 000元本金里，作為新的“本金”開始記取利息（這叫“復利”），到12月底時，一共轉存了3次，記取了3次復利，正好取出本息。

現在我們分別計算每期結束的本息和：

第一次存期到期的本息和：A1=本金+利息=1 000+1 000×a‰=1 000（1+a‰）；

第二次存期到期的本息和：A2=本金+利息=1 000×（1+a‰）+1 000×a‰×（1+a‰）=1 000×（1+a‰）2；

以此類推，第三次存期到期的本息和：A3=本金+利息=1 000×（1+a‰）3；

第四次存期到期的本息和：A4=本金+利息=1 000×（1+a‰）4；

通過觀察，發現A1、A2、A3、A4，構成一個等比數列，它的公比是（1+a‰）。我們可以按照等比數列，已知A1，和公比（1+a‰），運用數列的知識求數列的第4項的值，到期的本息和A=A1×（1+a‰）［4-1］= 1 000×（1+a‰）4，A和上述分析得出的A4相等，也就是兩次計算結果完全相同。

依據以上分析計算，我們得出定期轉存（復利計息）儲蓄，它的本息計算可以按照等比數列的通項公式，構建起這種銀行存款品種的本息和的數學計算模型是：本息和=每期存入金額×（1+利率）存期。（以下記做公式2。）

通過對以上兩個代表性的銀行存款儲蓄品種的分析，可以類推出這樣的結論，如果是單利計算的儲蓄品種，一般都可以應用等差數列建立數學模型，計算利息；如果按照復利支付利息的儲蓄品種，一般都可以通過等比數列建立數學模型，計算本息和，算出利息。

二、運用數列知識，分析日常理財收益，規劃科學的理財方案

以一個雙工薪（一個企業，一個老師）的家庭的薪金收入為例，做好理財方案的分析和規劃。收入來源一是工資收入，一人3 000元，一人4 000元；二是前三個季度績效考核工資3 000元；三是年末的績效收入10 000元。我們假設以每月4 000元為生活費，年末的10 000元作為全年花銷的備用金，其余家庭收入參與理財規劃，做一年的理財方案如下：

1.方案一：粗放的活期理財模式

現在的薪金發放，都是打在折（卡）上，粗心的家庭會積攢一年，到年底盤點后，再考慮提取資金，轉成高息理財產品。按照這個活期方案，我假定工資都是月初發放，工資收入每月存入3 000元，到12月末收益記作A1，季度績效月初發放，一共發放3次，每次3 000元，到12月末收益記作A2，年末獎金10 000元次年1月初發放，留做全年備用，收益記作A3。

按照中國銀行2014年公布的年利率值：活期0.35%，3個月定期2.6%，零存整取（整存零取）1.71%，半年定期2.8%，一年的定期3.25%。

計算家庭一年薪金理財收益：按照活期月利率=0.35%/12=0.029167%，計算的利息和是：A=A1+A2+A3，其中工資收入的活期利息按照公式（1）進行計算，A1=3 000×12×（12+1）×（1/2）× 0.029167%=60.25元；季度績效獎金的活期利息按照公式（1）進行計算，A2=3 000×3×（3+1）×（1/2）×（3×0.029167）%=15.75元；10 000元備用金的收益，相當于5 000元存6個月的活期利息，其計算模型：利息=存入金額×存期×月利率（推導過程略去），A3=5 000×6×0.029167%=8.75元。

通過以上計算出理財方案一，每年薪金收入產生的利息之和是：A=60.25+15.75+8.75=84.75元。

2.方案二：“工資零存整取+績效定期轉存+備用金整存零取”的理財模式

我們假定月初發放的工資，每月零存整取的方式存入3 000元，到12月末的收益記作A1，每季度初的3 000元績效獎，按照3個月的定期轉存，到12月末的收益記作A2，上年度的年末獎金10 000元，按照一年4次的整存零取，有計劃的季度資金備用方式，到12月末的收益記作A3。

計算家庭一年薪金理財收益的利息和是：A=A1+A2+A3，其中A1，工資的零存整取存款方式，利用（公式1）利息=每期存入金額×存期數×（存期數+1）×（1/2）×月利率］。月利率=1.71%/12=0. 1425%%。計算出A1=3000×12×（12+1）×（1/2）× 0.1425%=333.45元；

A2，績效獎金按照三個月的定期轉存的存款方式，到12月末，一季度的3 000元獎金經歷了3個存期，二季度的獎金經歷2個存期，三季度的獎金經歷1個存期，是復利計息，符合等比數列，按照通項公式建模。直接利用公式（2），本息和=每期存入金額*（1+利率）存期，三個月定期利率=2.6%/4=0.65%。計算的利息A2=3000×（1+0.65%）1+3000×（1+0.65%）2 +3 000×（1+0.65%）-9 000=117.5元。

A3，1 000元備用金年初整存，按照每季度末存款支取2 500元，支取4次，是單利計息。其符合等差數列關系，直接利用數學模型公式（1），計算其本息和=每期消費金額×消費期×（消費期+1）×（1/2）×利率，利率1.71%/4=0.4275%。計算出到期的利息A3=2 500×4×（4+1）×（1/2）×0.4275%=106.87元

通過以上計算出的理財方案二，一年薪金產生的利息是A=A1+A2+A3=333.45+117.5+106.87= 557.82元。

3.理財方案收益效果比較

一個家庭的一年薪金，如果按照方案一粗放的在銀行的工資卡上，算作存活期，方便取用，但只能達到錢在銀行的“保值”目的，利息收益太低了。方案二采取分類選擇相應的理財品種，通過運用數列方法分析計算的資金收益結果看，在既達到資金保值目的同時，又平均提高了家庭理財收益558%，經濟效益可觀。現做兩種理財方案的收益比較表如下：

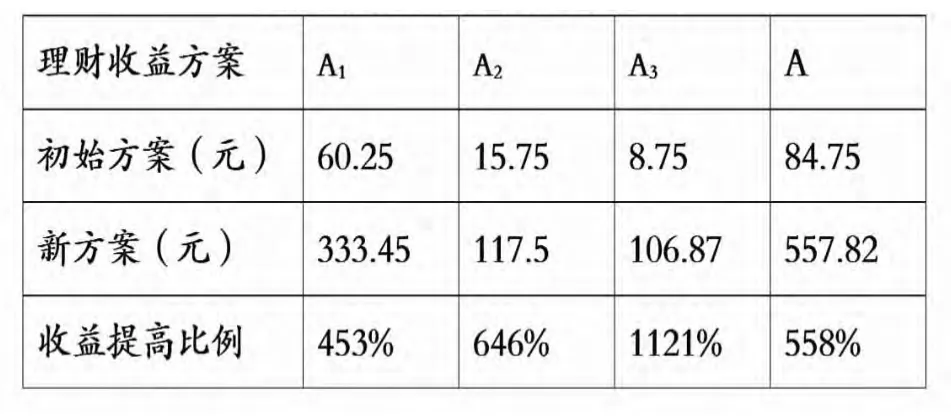
兩種理財方案的收益比較表（一）

通過這次對數列在家庭日常理財中應用的探究，既了解不同儲蓄品種的分類及利息計算方式的原理，更主要的是運用數列的公式，建立了利息計算的數學模型，運用這些方法分析論證了薪金的不同，理財方案的效益，這是數學知識解決實際生活問題的一個很好應用。