現金管理中的Baumol模型和Miller-Orr模型
吳松華
現金管理中的Baumol模型和Miller-Orr模型
吳松華
企業財務管理是對企業資金籌集和運用的管理,其重點是現金管理。現金資產是企業中流動性最強的資產,又是企業中盈利性最低的資產。因此,現金管理除做好日常現金流轉控制外,還需要控制好現金持有規模,確定最佳現金持有量。本文將介紹確定最佳現金持有量的兩種模型即Baumol模型和Mill-Orr模型,以供企業管理人員參考借鑒。
財務管理;現金管理;Baumol模型;Miller-Orr模型
現金是企業資產中流動性最強的,它具有普遍的可接受性,隨時可以有效地進行交易。財務管理上所講的現金指的使企業的貨幣資金,因此企業的庫存現金、銀行存款、見票即付的銀行票據等都屬于現金的內容。企業為滿足日常生產經營,需要持有一定數量的現金,但是現金資產又是企業中盈利性最低的資產,持有現金過多,就會降低企業盈利水平。因此,企業如有多余現金,則常用來購買為有價證券。以控制好現金持有規模,做到最佳現金持有量。有價證券變現能力強,當現金不足需要補充時,就出售有價證券取得現金。這樣有價證券就成為了現金的替代品。
下面本文將介紹確定最佳現金持有量的兩種模型——Baumol模型和Miller-Orr模型,供企業管理人員參考。
一、Baumol模型
1952年美國經濟學家William·Baumol提出了用以確定最佳現金持有量的Baumol模型。
利用Baumol模型確定最佳現金持有量,必須假定以下基本前提:(1)企業的現金流入量是穩定并可預測的。(2)企業的現金流出量是穩定并可預測的。(3)在預測期內,企業不會發生現金短缺,并可以通過出售有價證券來補充現金。在符合以上基本前提下,企業的現金流量可用圖1來表示。
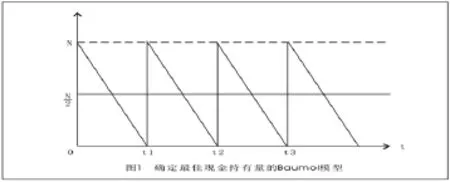
在圖1中,企業現金需求總量在一定時期內是確定的,企業的最佳現金持有量是N元,在一個周期t內均勻地耗用完,然后出售數量為N元的有價證券來補充現金,以后各個周期不斷重復。
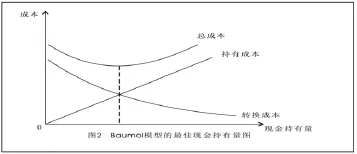
現金的持有成本與現金的持有量成正比,現金持有量越大,現金的持有成本就越高。而現金的轉換成本則和現金與有價證券的轉換次數密切相關,在全年現金需求總量一定情況下,現金持有量越大,現金與有價證券轉換次數就越少,所以,現金的轉換成本與轉換次數成正比,與現金持有量成反比。這樣,現金的持有成本與轉換成本就呈反方向變化。在現金需求總量一定的情況下,現金持有量越高,其持有成本就越大,而轉換成本則越小。因此,兩種成本之和最低時的現金持有量就是企業的最佳現金持有量。Baumol模型的最佳現金持有量可用圖2表示。
假設:C為現金的總成本;b為現金與有價證券的轉換成本;T為一定時期的現金需求總量;N為最佳現金持有量;i為有價證券的利息率。則持有現金的總成本可用如下公式來表示:
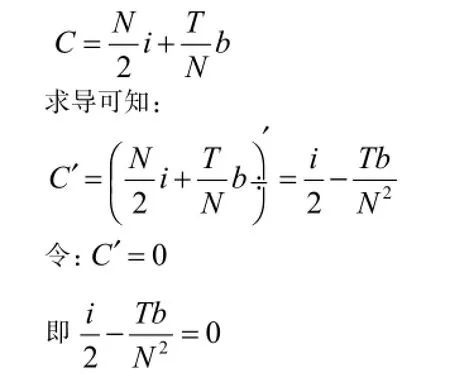
求得最佳現金持有量為:
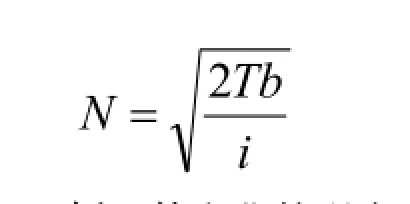
例1.某企業的現金流量穩定,預計全年的現金需求總量為200000元,每次出售有價證券的轉換成本為400元,有價證券的年利率為10%。采用Baumol模型確定該企業的最佳現金持有量。
根據Baumol模型的公式,可計算出該企業最佳現金持有量N為:
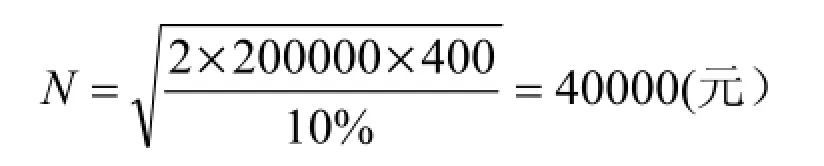
所以,該企業最佳現金持有量為400000元。
Baumol模型用來確定最佳現金持有量比較簡單明了,但是由于其假定現金的流出量穩定不變,實際當中這樣的情況很少有。
二、Miller-Orr模型
1966年美國經濟學家Merton Miller和Daniel Orr首次創建了一種能在現金流入量和流出量隨機波動情況下確定最佳現金持有量的Miller-Orr模型。對企業來講,現金實際的需求量往往波動大且難以預知,但企業可以依據歷史數據和現實情況,測算出一個現金持有量的合理范圍,即制定出現金持有量的上、下限,將現金持有量控制在合理范圍之內。當現金持有量達到范圍上限時,就用現金購買有價證券,使持有量下降;當持有量下降到范圍下限時,則將有價證券兌回現金,使現金持有量上升。若現金持有量在上下限合理范圍之內,則不必進行相互的轉換。這種對現金持有量的控制,可用圖3表示:
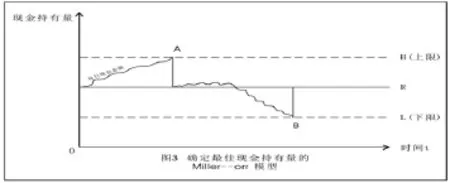
圖3中,虛線H為持有量的上限,虛線為L為持有量的下限,實線R為最優現金返回線。從圖中可以發現,企業的現金持有量是隨機波動起伏的,當其到A點時,即達到控制持有量的上限,此時企業應該購入有價證券,讓持有量下降到R線,即現金返回線;當持有量下降至B點時,即達到控制持有量的下限,此時應該出售有價證券取得現金,使其持有量回升至R線的水平。現金持有量在合理控制范圍內的上下限之間的波動變化,不需要進行轉換。圖中的上限H,現金返回線R,可按下
列公式計算:
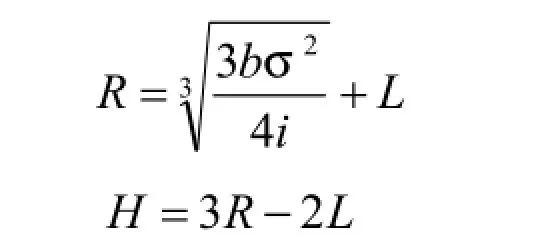
公式中:b—每次出售有價證券的轉換成本;
i—有價證券的月利息率;
σ—預期每日現金余額變化的標準差(可根據歷史數據測算)
而下限L則需要根據企業每日的最低現金需要,企業管理者愿意冒缺少現金風險的程度等因素的影響來確定。
例2.假定某企業持有的有價證券為9%的年利率,固定轉換成本為每次60元,企業認為在任何時候其銀行活期存款及庫存現金均不能低于1000元,又根據以往資料測算出現金余額波動的標準差為800元。最優現金返回線R,現金控制上限H的計算如下:
有價證券日利率=9%÷360=0.025%
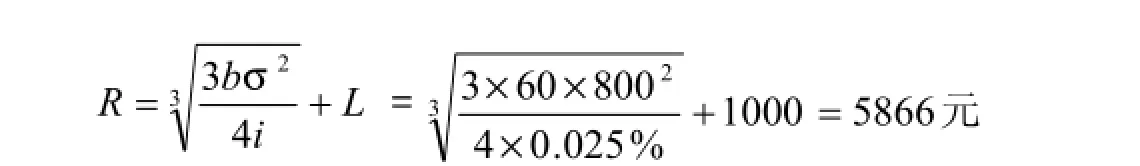
H=3R-2L=3×5866-2×1000=15598
這樣,當企業的現金持有量達到15598元時,即應以9732元(15598-5866)的現金去購買有價證券,使持有量下降到5866元;當企業的持有量降至1000元時,則應兌換4866元(5866-1000)的有價證券,使持有量回升到5866元。
Miller-Orr模型建立在企業的現金未來需求總量和收支不可預測的前提下,因此計算出來的現金持有量相對比較保守。
三、結語
以上介紹了Baumol模型和Miller-Orr模型的應用前提、計算公式、計算方法以及優缺點等,隨著我國證券市場不斷的完善,上述兩種模型在企業管理特別是現金管理中將發揮重要作用。
[1](美)詹姆斯·范霍思,約翰·瓦霍維奇.《現代企業財務管理》[M].經濟科學出版社.1988年版.
[2](美)斯蒂芬·羅斯,倫道夫·威期特菲爾德.《公司理財》[M].機械工業出版社.2004年版.
[3]湯谷良,王化成主編.《企業財務管理學》[M].經濟科學出版社.2000年版.
[4]2012年度注冊會計師全國統一考試輔導教材.《財務成本管理》[M].中國財政經濟出版社.2012年版.
(作者單位:咸寧職業技術學院)

