兩類3正則圖中的完美匹配數*

唐保祥，任 韓

(1.天水師范學院數學與統計學院,甘肅 天水 741001；2.華東師范大學數學系,上海 200062)

圖的完美匹配的理論在很多領域有廣泛應用，例如:積和式在計算機科學，特別是計算復雜性理論中有重要的地位，二分圖的完美匹配的數目可以方便地表示為計算積和式的值；共軛分子圖是否具有完美匹配對芳香族系統的穩定性是極其重要的；圖的完美匹配數也是估計共振能量和π—電子能量，計算鮑林鍵級的重要指標等[1-5]。遺憾的是，1979年Valiant證明了，一個圖(即使是偶圖)的完美匹配計數是NP-難問題[6]，若NP≠P，即這個問題不存在多項式解法獲得最優解。Lovász和Plummer曾提出關于完美匹配計數的一個猜想：任意2邊連通3正則圖都有指數多個完美匹配[7]。文獻[8]中給出了3類2邊連通3正則的圖，它們都有指數多個不同的完美匹配。本文給出了2類2邊連通3正則圖美匹配數目的計算公式,驗證了Lovász 和Plummer 猜想在這2類圖上的正確性。

1 相關概念

定義1 若圖G的兩個完美匹配M1和M2中有一條邊不同，則稱M1和M2是G的兩個不同的完美匹配。

圖1 3-nC6圖

設2n個長是4的圈為Ci1:ui1ui2ui3ui4ui1，Ci2:vi1vi2vi3vi4vi1(i=1,2,…,n)。連接圈Ci1和Ci2的頂點ui1與vi1，ui3與vi3；連接Ci1，Ci2與Ci+1,1，Ci+1,2的頂點ui2與ui+1,4，與(i=1,2,…,n-1)；再連接圈C11和C12的頂點u14與v14，圈Cn1和Cn2的頂點un2與vn2。這樣所得的圖記為2-2nC4，如圖2所示。

圖2 2-2nC4圖

2 主要結果及其證明

定理1σ(n)表示圖3-nC6的完美匹配的數目，則

證明圖3-nC6是3正則3連通圖，顯然存在完美匹配。σ(n)表示圖3-nC6的完美匹配數。設圖G，S?V(G)，記G′=G-S為圖G刪除S中的頂點所得到的圖。設S1={u11,u15,u16,v11,v15,v16},S2={u11,u14,u15,u16,v11,v14,v15,v16},S3={u11,u12,u15,u16,v11,v12,v15,v16},G1=3-(n+1)C6-S1，G2=3-(n+1)C6-S2，G3=3-(n+1)C6-S3，G4=3-(n+1)C6-{u16,v16}，G5=3-nC6-{u15,u16}，G6=3-nC6-{u11,u16}，圖G1,G2,…,G6如圖3-8所示。

圖3 G1圖

圖4 G2圖

圖5 G3圖

圖6 G4圖

圖7 G5圖

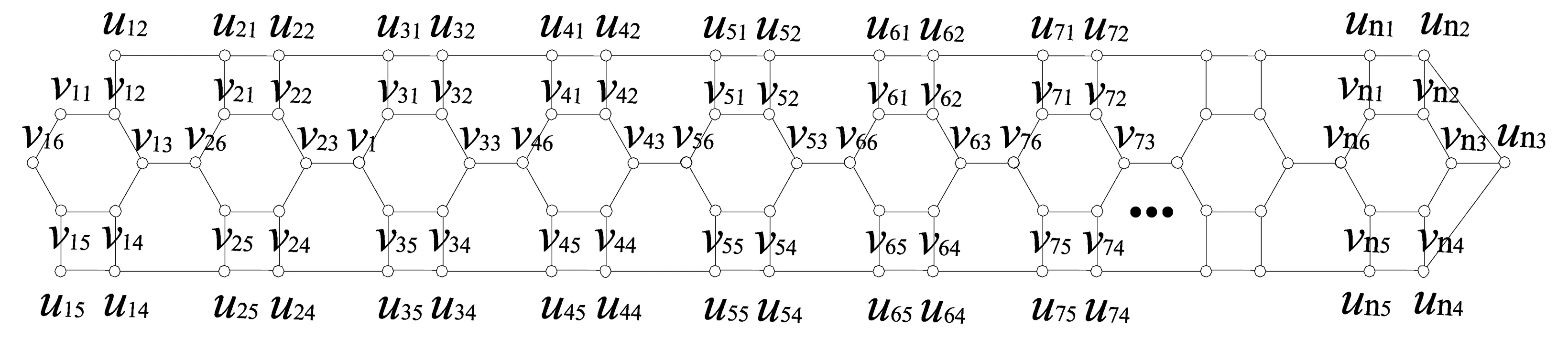
圖8 G6圖

圖G1,G2,…,G6均含n個6圈，顯然都有完美匹配，G2?G3，G5?G6。設圖G1，G2,…,G6的完美匹配數分別為g(n)，h(n)，δ(n)，α(n)，β(n)，γ(n)，則h(n)=δ(n)，β(n)=γ(n)。

由β(n)的定義，圖G1含邊u12u21,v12v13,u14v14的完美匹配數為β(n)，由δ(n)的定義圖G1含邊u12u21的完美匹配數為δ(n),δ(n)=h(n)，所以

g(n)=β(n)+h(n)

(1)

由β(n)的定義，圖G2含邊u12u21,v12v13的完美匹配數為β(n)，由α(n)的定義圖G2含邊u12v12,v13v16的完美匹配數為α(n-1)，所以

h(n)=α(n-1)+β(n)

(2)

由h(n)的定義，圖G3含邊u11u12,v11v12,u15v15的完美匹配數為h(n)，由α(n)的定義圖G3含邊u11u12,v11v12,v13v26,v15v14,u15u14的完美匹配數為α(n-1)，由g(n)的定義圖G3含邊u11v11,v15u15的完美匹配數為g(n)，由h(n)的定義圖G3含邊u11v11,v15v14,u15u14的完美匹配數為h(n)，所以

α(n)=2h(n)+g(n)+α(n-1)

(3)

由β(n)的定義，圖G5含邊u11u12,v11v16,v12v13,v15v14,u14u25的完美匹配數為β(n-1)；由h(n)的定義，圖G5含邊u11u12,v11v12,v16v15的完美匹配數為h(n-1)；由g(n)的定義，圖G5含邊u11v11,v16v15的完美匹配數為g(n-1)。所以

β(n)=g(n-1)+h(n-1)+β(n-1)

(4)

由γ(n)的定義，圖3-nC6含邊u11u16的完美匹配數為γ(n)；由α(n)的定義圖3-nC6含邊u16v16的完美匹配數為α(n-1)，由β(n)的定義，圖3-nC6含邊u15u16的完美匹配數為β(n)，β(n)=γ(n)。所以

σ(n)=2β(n)+α(n-1)

(5)

由(1)-(5)式得

σ(n)=2g(n-1)+2h(n-1)+

2β(n-1)+α(n-1)

(6)

σ(n)=8β(n-1)+4α(n-2)+α(n-1)

(7)

由(4)和(6)式得

2β(n)=σ(n)-α(n-1)

(8)

由(7)和(8)式得

σ(n)=4σ(n-1)+α(n-1)

(9)

由(1)，(2)，(3)和(8)式得

α(n)=2σ(n)+2α(n-1)

(10)

由(9)和(10)式得

σ(n)=6σ(n-1)+2α(n-2)

(11)

σ(n-1)=4σ(n-2)+α(n-2)

(12)

(11)-2×(12)式得

σ(n)=8σ(n-1)-8σ(n-2)

(13)

圖9 3-1×C6圖

如圖9所示，圖3-1×C6含邊u11u16,v11v16的完美匹配有5個，含邊u11u16,v11v12,u12u13,v13v14,u14u15,v15v16完美匹配有1個，含邊u16v16的完美匹配有8個，含邊u16u15,v16v15的完美匹配有5個，含邊u16u16,v15v14,u14u13,v13v12,u11u12,v11v16的完美匹配有1個，所以σ(1)=20。

圖10 G7圖

如圖10所示，圖G7含邊u11u12,v11v12,v13v26,v15v14,u15u14的完美匹配有8個， 含邊u11u12,v11v12,v13v26,v15u15,v14u14的完美匹配有8個，含邊u11u12,v11v12,v13v14,v15u15,u14u25,v21v26,u21u22,v22v23,u23u24,v24v25的完美匹配有1個，含邊u11u12,v11v12,v13v14,v15u15,u14u25,v25v26的完美匹配有5個，含邊u11v11,u12v12,v13v26,u14v14,u15v15的完美匹配有8個， 含邊u11v11,u12v12,v13v14,v15u15,u14u25,v21v26,u21u22,v22v23,u23u24,v24v25的完美匹配有1個，含邊u11v11,u12v12,v13v14,v15u15,u14u25,v25v26的完美匹配有5個，含邊u11v11,u12v12,v13v26,v15v14,u15u14的完美匹配有8個，含邊u11v11,u12u21,v12v13,v15u15,v14u14,v21v26的完美匹配有5個，含邊u11v11,u12u21,v12v13,v15u15,v14u14,v25v26,u25u24,v24v23,u23u22,v22v21的完美匹配有1個，含邊u11v11,u12u21,v12v13,v15v14,u15u14,v26v21的完美匹配有5個，含邊u11v11,u12u21,v12v13,v15v14,u15u14,v25v26,u25u24,v24v23,u23u22,v22v21的完美匹配有1個， 所以，α(1)=56。因此，由(9)式得σ(2)=136。

線性遞推式(13)滿足α(1)=56，σ(2)=136的解為

定理2ψ(n)表示圖2-2nC4的完美匹配的數目，則ψ(n)=9·5n-1。

證明圖2-2nC4是3正則2連通圖，顯然存在完美匹配。ψ(n)表示圖2-2nC4的完美匹配數。為了求ψ(n)，先定義一個圖G8和G9，并求其完美匹配的數目。刪除圖2-2nC4的邊u14v14都得到的圖記為G8；將長為6的圈u1v1w1w2v2u2u1的頂點v1,v2與圈C11和C12的頂點u14,v14分別連接一條邊得到的圖記為G9，如圖11-12所示。

圖11 G8圖

圖12 G9圖

顯然圖G8和G9均有完美匹配，圖G8和G9的完美匹配數分別記為λ(n)和π(n)。

圖2-2nC4的完美匹配按飽和頂點u14的情況可劃分為如下7種情形。

情形1：由λ(n)的定義，圖2-2nC4含邊u11u14,v11v14,u12u13,v12v13的完美匹配數為λ(n-1)；

情形2：由π(n)的定義，圖2-2nC4含邊u11u14,v11v14,u12u24,v12v24,u13v13的完美匹配數為π(n-2)；

情形3：由λ(n)的定義，圖2-2nC4含邊u11u14,u12u13,v11v12,v13v14的完美匹配數為λ(n-1)；

情形4：由λ(n)的定義，圖2-2nC4含邊u11u12,u13u14,v12v13,v11v14的完美匹配數為λ(n-1)；

情形5：由λ(n)的定義，圖2-2nC4含邊u11u12,u13u14,v11v12,v13v14的完美匹配數為λ(n-1)；

情形6：由π(n)的定義，圖2-2nC4含邊u11v11,u13u14,v13v14,u12u24,v12v24的完美匹配數為π(n-2)；

情形7：由π(n)的定義，圖2-2nC4含邊u14v14的完美匹配數為π(n-1)。

故

ψ(n)=4λ(n-1)+π(n-1)+2π(n-2)

(14)

求λ(n)。圖G8的完美匹配按飽和頂點u14的情況可劃分為如下6種情形。

情形1：由λ(n)的定義，圖G8含邊u11u14,v11v14,u12u13,v12v13的完美匹配數為λ(n-1)；

情形2：由π(n)的定義，圖G8含邊u11u14,v11v14,u12u24,v12v24,u13v13的完美匹配數為π(n-2)；

情形3：由λ(n)的定義，圖G8含邊u11u14,u12u13,v11v12,v13v14的完美匹配數為λ(n-1)；

情形4：由λ(n)的定義，圖G8含邊u11u12,u13u14,v12v13,v11v14的完美匹配數為λ(n-1)；

情形5：由λ(n)的定義，圖G8含邊u11u12,u13u14,v11v12,v13v14的完美匹配數為λ(n-1)；

情形6：由π(n)的定義，圖G8含邊u11v11,u13u14,v13v14,u12u24,v12v24的完美匹配數為π(n-2)。故

λ(n)=4λ(n-1)+2π(n-2)

(15)

再求π(n)。圖G9的完美匹配按飽和頂點u1的情況可劃分為如下3種情形。

情形1：由λ(n)的定義，圖G9含邊u1v1,u2v2,w1w2的完美匹配數為λ(n)；

情形2：由λ(n)的定義，圖G9含邊u1u2,v1w1,v2w2的完美匹配數為λ(n)；

情形3：由π(n)的定義，圖G9含邊u1u2,v1u14,v2v14,w1w2的完美匹配數為π(n-1)。

故

π(n)=2λ(n)+π(n-1)

(16)

由(14)和(15)式，得

ψ(n)=λ(n)+π(n-1)

(17)

由(14)和(16)式，得

ψ(n)=6λ(n-1)+3π(n-2)

(18)

由(17)和(18)式，得

ψ(n)=3ψ(n-1)+3λ(n-1)

(19)

由(15)和(17)式，得

λ(n)=2ψ(n-1)+2λ(n-1)

(20)

由(19)和(20)式，得

ψ(n)=3ψ(n-1)+6ψ(n-2)+6λ(n-2)

(21)

由(19)式，得

ψ(n-1)=3ψ(n-2)+3λ(n-2)

(22)

(21)-2×(22)式，得ψ(n)=5ψ(n-1)。易知n=1時，圖2-2×1C4的完美匹配數為9，故ψ(1)=9，所以ψ(n)=9·5n-1。

參考文獻：

[1] KASTELEYN P W.Dimmer statistics and phase transition [J].Math Phys,1963,4:287-293.

[2]VALIANT L G.The complexity of computing the permanent [J].Theoretical Compute Science,1979,8(2):189-201.

[3]CYVIN S J,GUTMAN I.Kekué structures in Benzennoid hydrocarbons [M].Berlin:Springer Press,1988.

[4]PLUMMER M D.Matching theory-a sample:form denies to the present [J].Discrete Mathematics,1992,100:177-219.

[5]FOURNREI J C.Combinatorics of perfect matchings in planar bipartite graphs and application to tilings [J].Theoretical Computer Science.2003,303:333-351.

[6]VALIANT L G.The complexity of computing the permanent [J].Theoretical Compute Science,1979,8(2):189-201.

[8]唐保祥,任韓.幾類圖完美匹配的數目[J].南京師范大學學報:自然科學版,2010,33(3):1-6.