高速磁懸浮電機轉子低頻振動干擾觀測與抑制研究
劉 健, 鄭世強, 房建成
(1.北京航空航天大學慣性技術重點實驗室, 北京 100191; 2.新型慣性儀表與導航系統技術國防重點學科實驗室, 北京 100191)
引 言
由于主動磁軸承(Active Magnetic Bearing)具有無機械磨損、無需潤滑、可主動振動控制等優(yōu)點[1],得到了越來越多的研究和應用,隨著磁懸浮技術的日益成熟,磁懸浮電機被廣泛應用到諸如磁懸浮鼓風機、磁懸浮壓縮機等高速旋轉機械裝備領域。相比傳統的旋轉機械裝備,磁懸浮電機通常需要運行在高轉速下才能提升整機系統的節(jié)能效率等性能指標。隨著轉速的提高,磁懸浮電機轉子在高速時的失穩(wěn)問題也逐漸凸顯,提高磁懸浮轉子在高速時的穩(wěn)定性,保證磁懸浮電機在高速時的穩(wěn)定運轉是磁懸浮電機要解決的一個重要問題。磁懸浮電機轉子在高速時失穩(wěn),其主要表征就是轉速同頻分量的增大和低頻振動的增加,前者可以利用動平衡技術來解決。在保證磁懸浮轉子具有較好的動平衡即在高速時具有較小的轉速同頻分量的情況下[2,3],低頻振動成為影響其高速穩(wěn)定性的一個至關重要的因素,抑制磁懸浮轉子在高速時的低頻振動,可以有效提高其在高速時的穩(wěn)定性。
對于大慣量扁平轉子因陀螺效應引起的低頻振動,相關領域的研究者進行了相關方面的研究[4,5],也提出了有效的解決方法;而對于磁懸浮電機轉子在高速時的低頻振動,研究相對較少。現在大多數研究者選用先進控制算法來提高磁懸浮轉子高速時的穩(wěn)定性[6,7],抑制低頻振動,但很多先進控制算法運算復雜,再加上現用控制器在運算位數、處理速度等方面的限制,此方法不但不能有效抑制其低頻振動,還會給系統帶來更大的相位滯后,加劇其在高速時的不穩(wěn)定。Jugo等利用頻域模型對磁懸浮轉子高速穩(wěn)定性進行了研究[8,9],分析指出磁懸浮轉子在高速時低頻振動的增大,造成了系統的失穩(wěn)。但該文章僅限于理論分析,沒有提出有效的解決方案。
本文利用改進型干擾觀測器(Improved Disturbance Observer, IDOB)對磁懸浮電機轉子在高速時的低頻振動進行觀測[10],并在控制器中對其進行抑制。對100 kW磁懸浮電機運行在24 000 r/min轉速時進行了實驗驗證。實驗表明,該方法有效地克服了磁懸浮電機轉子高速時形變的影響,對低頻振動有很好的觀測抑制作用,極大提高了磁懸浮電機轉子高速時的穩(wěn)定性。
1 IDOB原理分析
IDOB的實質為改進型干擾觀測器,傳統的干擾觀測器需要實際系統的逆模型,逆模型的精度影響了整個觀測器的精度,且需要一個高階的低通濾波器來提高觀測精度,低通濾波器的階次越高,觀測精度越高,但系統的魯棒穩(wěn)定性越低,工程應用越難實現[11,12],兩者之間的矛盾難以調和,對磁懸浮電機轉子系統而言,低速時的模型和高速時模型之間存在一定的差異,其標稱模型和逆模型很難精確獲得,這使得傳統干擾觀測器不適用于磁懸浮轉子系統高速時的低頻振動觀測抑制。為此,需對傳統的干擾觀測器進行優(yōu)化,使其適合磁懸浮高速電機轉子系統。
將磁懸浮電機高速時的低頻振動等效為一種低頻干擾,設其可由下式進行估計
(1)
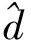
對于被控系統而言,設其傳遞函數為
(2)
將式(3)帶入式(1)可得
(4)
由于磁懸浮電機轉子高速時的模型誤差,bm與λm,βn與an之間必然存在誤差,設bm-λm=Δbm,βn-an=Δan,則式(4)的頻域形式可表示為
(5)
磁懸浮電機轉子在高速時的振動具有低頻性,ω很小,s可以忽略,針對此特性,式(5)可以進一步簡化為
(6)
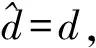
針對現用磁懸浮電機轉子的現狀,實驗中,對式(1)的m和n都選取為1,對低頻振動進行觀測,式(1)可化為

(7)
對式(7)進行拉普拉斯變換,可得
(8)
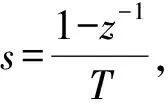
(9)
式中y(t)為當前時刻AD采樣值,y(t-1)為上一時刻AD采樣值,u(t)為當前時刻PID運算輸出值。由此可見,此改進型干擾觀測器相對于傳統的干擾觀測器,不僅更適于低頻量的觀測,而且更易于工程實現應用,具有很強的實用價值。
2 系統仿真分析
為了驗證帶有IDOB的主動磁軸承系統對低頻振動的抑制效果,以原離散PID磁軸承控制系統為參考,將帶有IDOB的主動磁軸承控制系統對低頻振動的抑制效果與未加IDOB的原離散PID控制系統的抑制效果作對比。帶有IDOB的整個主動磁軸承控制系統的仿真原理框圖如圖1所示。
圖1中,實線框中的部分就是在未加IDOB時,主動磁軸承控制系統的仿真原理框圖。首先對未加IDOB的主動磁軸承控制系統進行分析。
從轉頻輸入端到位移輸出端的系統傳遞函數為
(10)
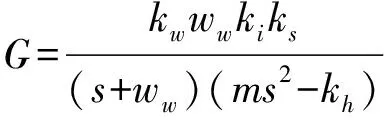
IDOB部分為圖1中雙點畫線框內的部分,加入該部分后,圖1整個框圖是帶有IDOB的主動磁軸承控制系統仿真原理框圖,對整個原理框圖的分析如下。帶有IDOB的主動磁軸承控制系統,其從轉頻輸入端到位移輸出端的系統傳遞函數為
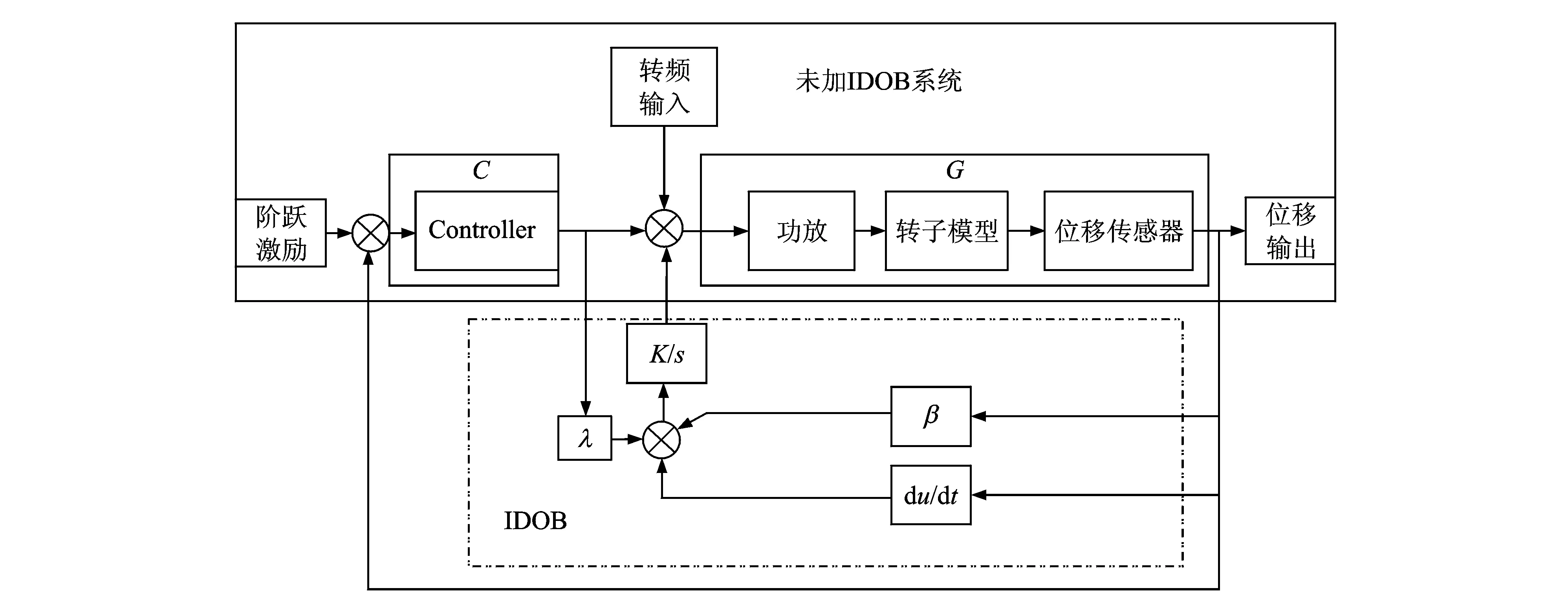
圖1 加IDOB的主動磁軸承控制系統仿真框圖
(11)
式中G和C與式(10)相同,K,β和λ為IDOB中的3個控制參數。
根據式(10)和(11)的傳遞函數,利用表1所示的仿真參數,可以得到未加IDOB的主動磁軸承系統與加IDOB的主動磁軸承系統在低頻段(2~100 Hz)的幅頻特性。
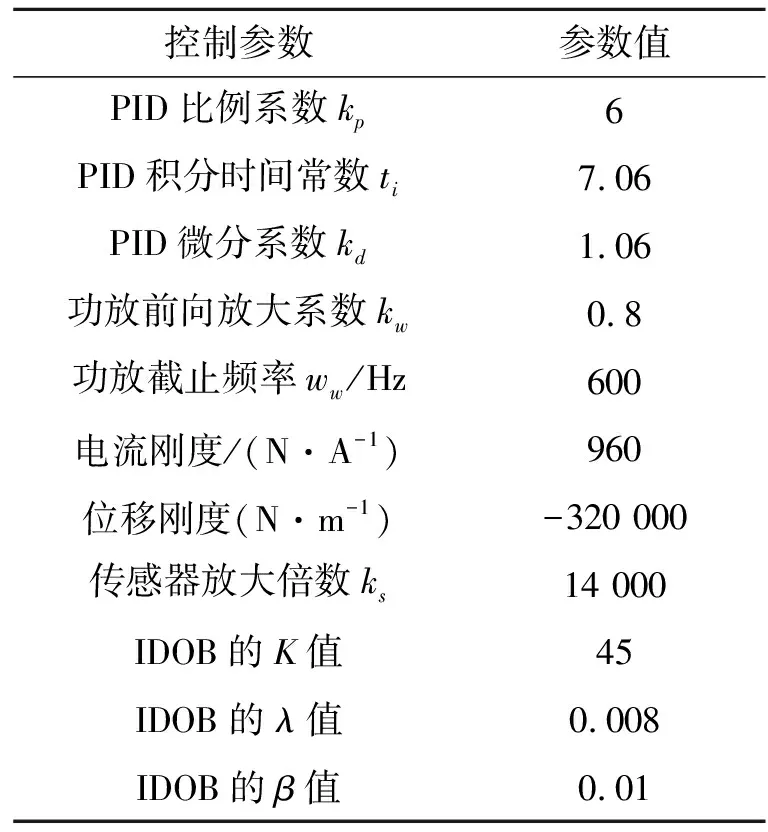
表1 Simulink仿真參數
未加IDOB的主動磁軸承系統與加IDOB的主動磁軸承系統低頻段的幅頻特性對比如圖2所示。
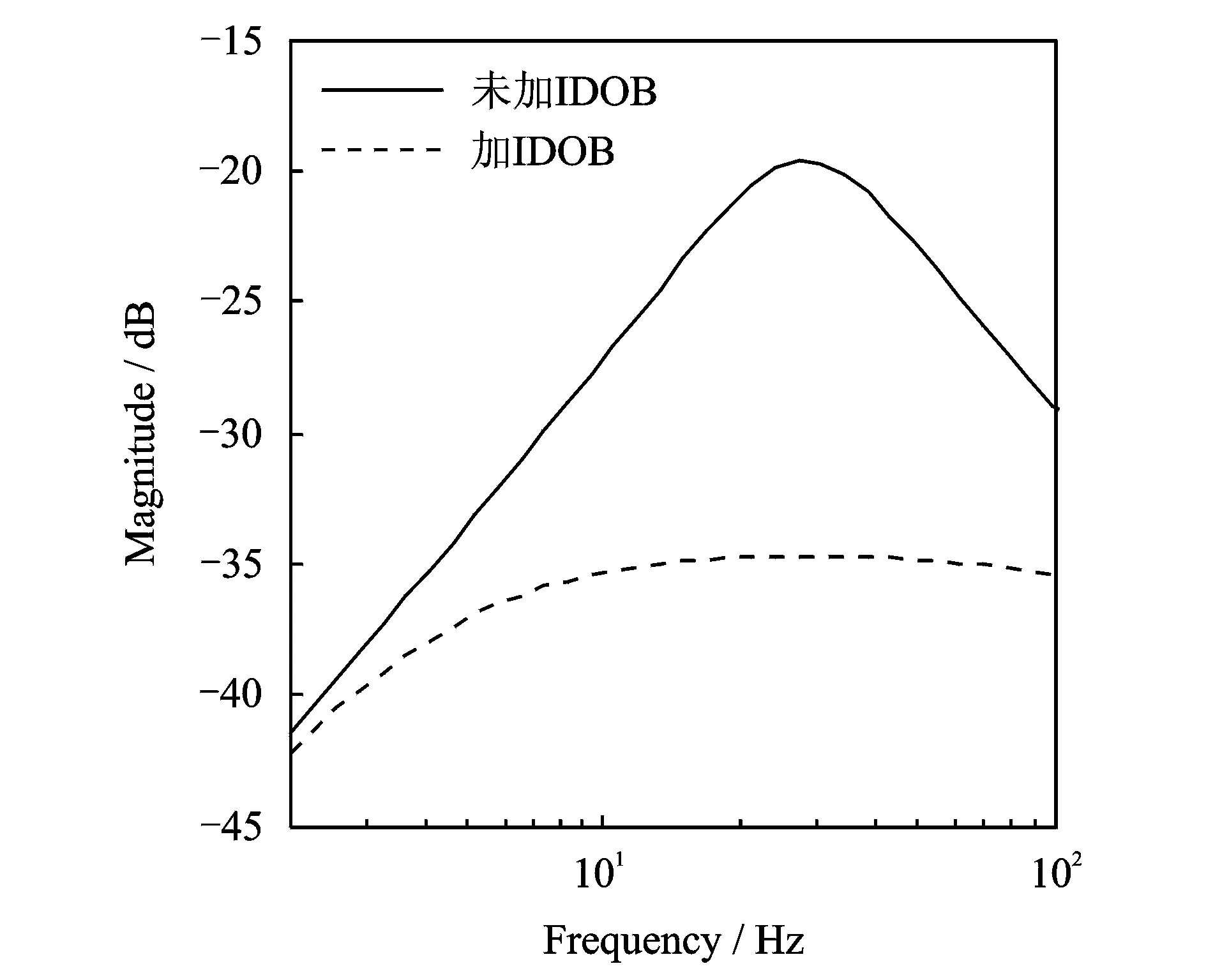
圖2 未加IDOB系統與加IDOB系統低頻段幅頻特性對比圖
從圖2的幅頻特性對比可以看出,加IDOB的主動磁軸承控制系統較未加IDOB的主動磁軸承控制系統,在2~100 Hz的低頻頻段范圍內,對低頻振動的幅值有更有效的衰減作用。
仿真系統中,階躍信號初始值為0,在仿真時刻為1時,階躍信號變?yōu)?,在系統外部輸入一個幅值為0.5,頻率為600 Hz的正弦信號作為主動磁軸承轉子的轉頻量,未加IDOB的主動磁軸承控制系統轉子位移與加IDOB的主動磁軸承控制系統轉子位移仿真對比圖如圖3所示。
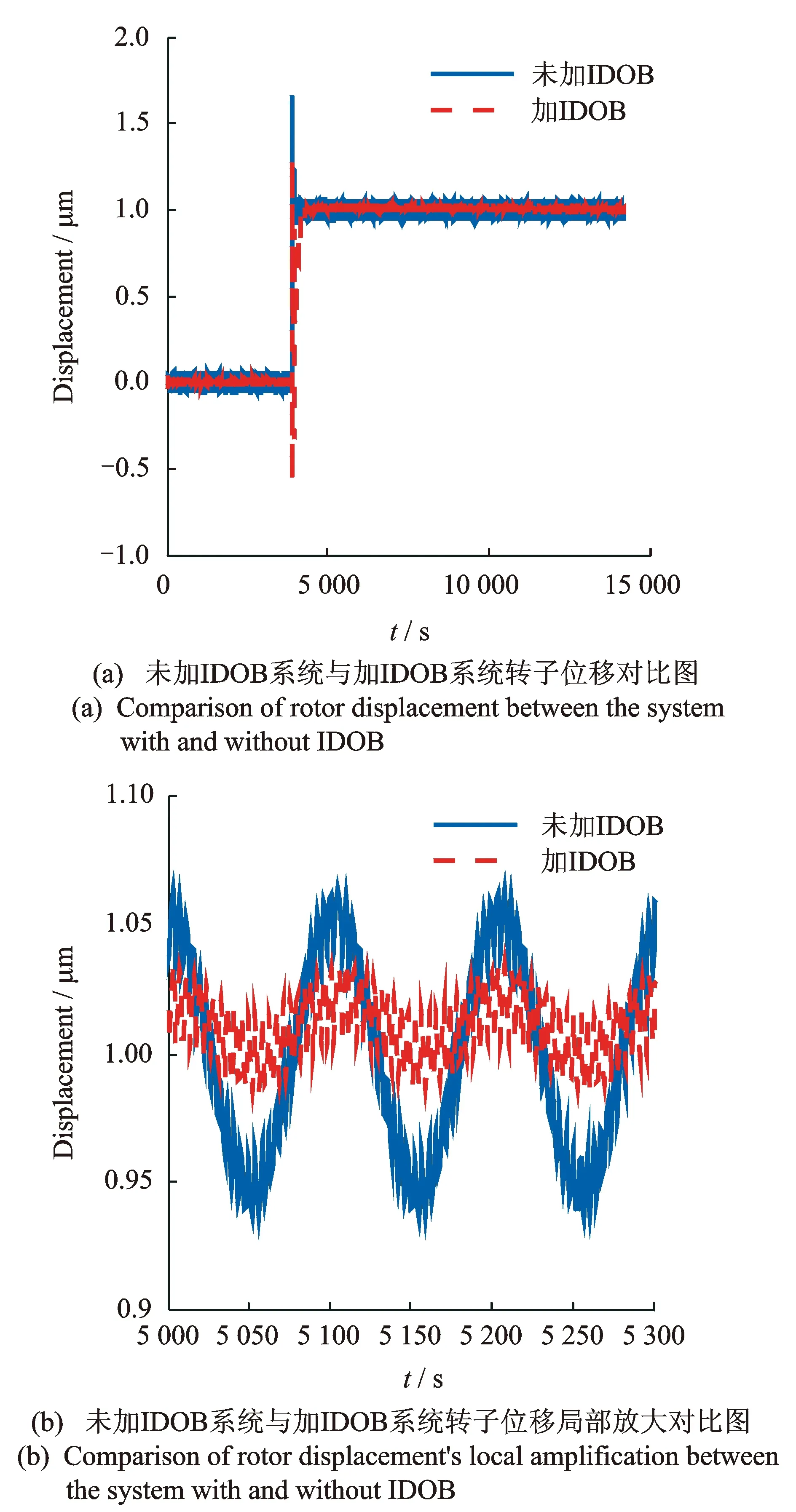
圖3 未加IDOB系統與加IDOB系統轉子位移對比圖
由圖3(a)可以看出,加IDOB的主動磁軸承控制系統相對于未加IDOB的主動磁軸承控制系統,對低頻振動有更好的抑制效果。
圖3(b)是主動磁軸承轉子達到1的穩(wěn)態(tài)時,取[5 000,5 300]時間段內波形的局部放大圖。由圖3(b)的穩(wěn)態(tài)局部放大圖可以得出,加IDOB的主動磁軸承轉子低頻振動量約為0.06,未加IDOB主動磁軸承轉子低頻振動量約為0.18,相對于原系統,加入IDOB的主動磁軸承系統,轉子低頻振動量減小了0.12,減小為原系統的33.3%,可見,加入IDOB的系統對于主動磁軸承轉子的低頻振動具有更好的抑制效果。
3 穩(wěn)定性分析
加入IDOB的主動磁軸承轉子系統,其穩(wěn)定性受K,λ和β三個參數的影響,隨著K的增大,式(11)傳遞函數的零極點分布趨勢變化如圖4所示。
由圖4可以看出,隨著K值的增大,系統出現了右半平面的極點,系統不再穩(wěn)定,其臨界穩(wěn)定K值為57。
隨著λ的增大,式(11)傳遞函數的零極點分布趨勢變化如圖5所示。
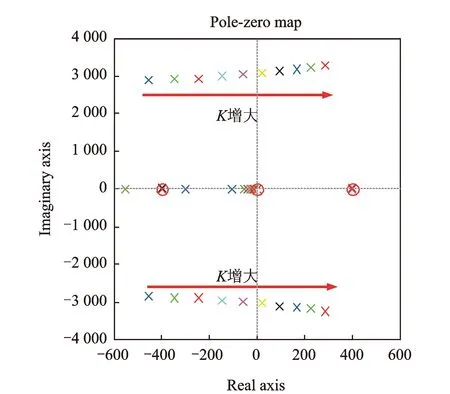
圖4 K增大系統零極點分布趨勢變化圖
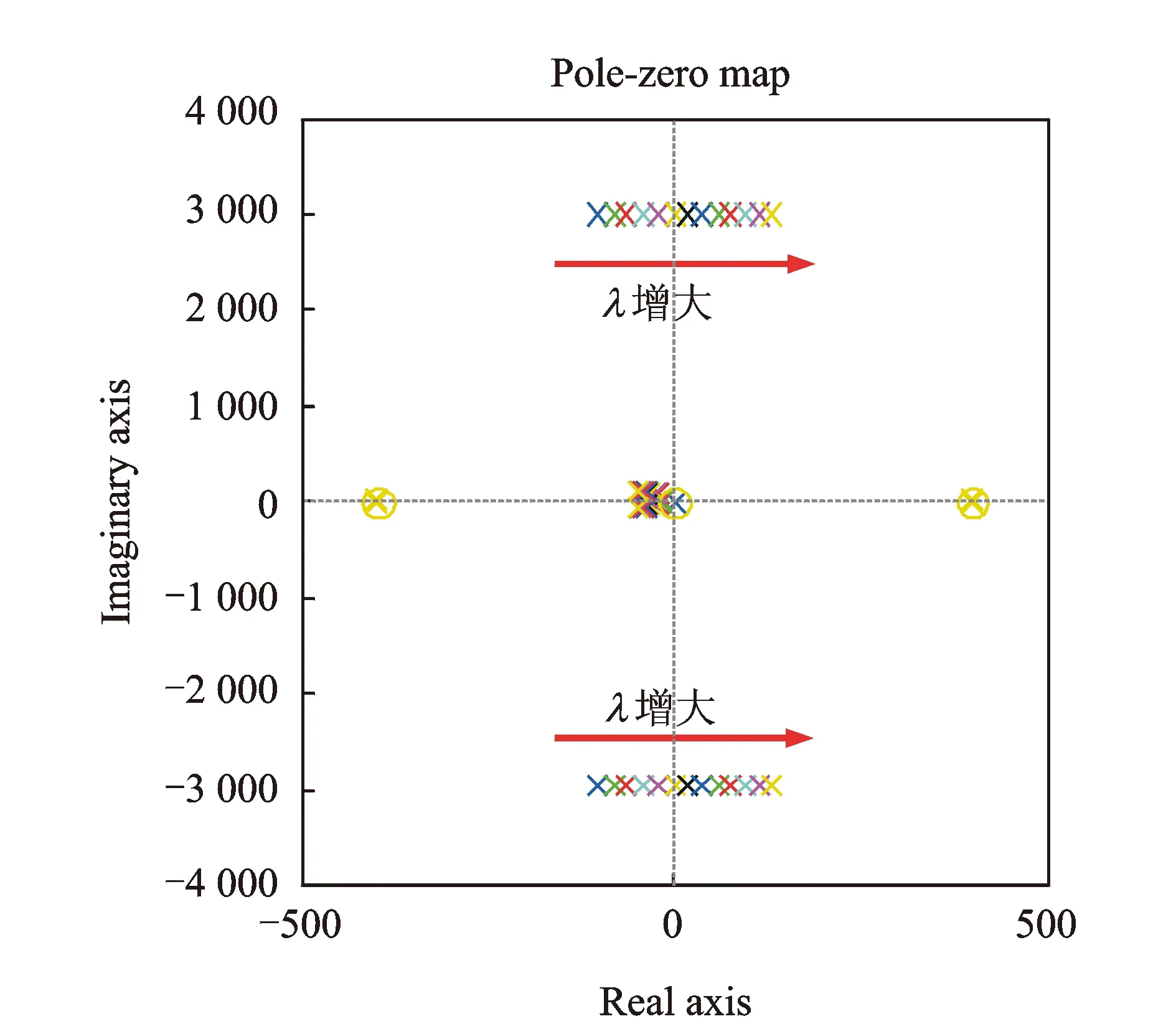
圖5 λ增大系統零極點分布趨勢變化圖
由圖5可以看出,隨著λ的增大,系統出現了右半平面的極點,系統不穩(wěn)定,其臨界穩(wěn)定的λ值是5.1。
隨著β增大,式(11)傳遞函數的零極點分布趨勢變化如圖6所示。
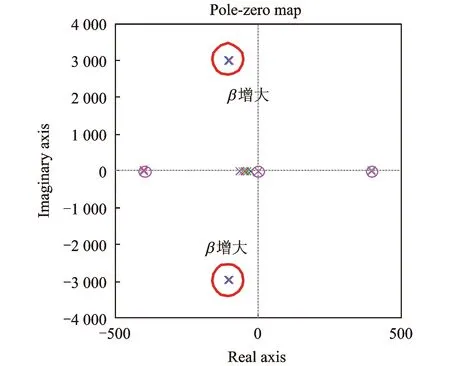
圖6 β增大系統零極點分布趨勢變化圖
由圖6可以看出,β的變化不影響主動磁軸承轉子系統零極點分布,也不影響系統的穩(wěn)定性。
綜上所述,加入IDOB后主動磁軸承轉子系統的穩(wěn)定性隨著K和λ的增大而降低,K的取值在[0,57]之間,λ的取值在[0,5.1]之間時,系統是穩(wěn)定的,β值的變化基本不影響系統穩(wěn)定性。
4 實驗驗證
為了驗證IDOB的低頻振動抑制效果,以100 kW電機為實驗平臺,在24 000 r/min轉速時,做了對比實驗驗證。
實驗中使用的100 kW電機是無刷直流電機,該電機是4極電機,采用4極分布式繞組,永磁體表貼的結構形式,電機控制采用的是兩相導通,三相六狀態(tài)的控制方式;該電機的磁軸承是純電磁磁軸承,有兩個徑向磁軸承,分別位于電機的兩端,一個軸向磁軸承位于電機的末端,磁軸承控制采用的是五自由度全懸浮的方式,兩個徑向磁軸承負責四個徑向自由度的懸浮,一個軸向磁軸承負責一個軸向自由度的懸浮。實驗中使用的100 kW磁懸浮電機的主動磁軸承系統的設計參數如表2所示。
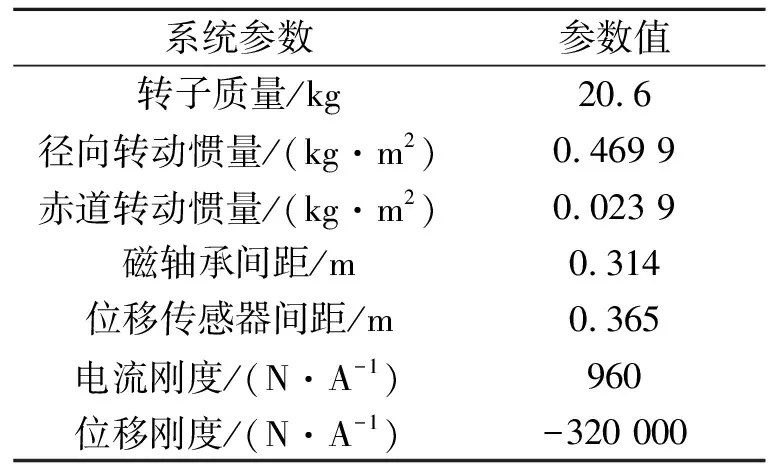
表2 100 kW磁懸浮電機主動磁軸承系統參數
實驗中使用的100 kW磁懸浮電機磁軸承系統的徑向控制參數如表3所示。
在選取上述IDOB參數的情況下,主動磁軸承轉子閉環(huán)系統的零極點分布如圖7所示。
由圖7可以看出,在選取上述IDOB參數的情況下,主動磁軸承轉子閉環(huán)系統是穩(wěn)定的,在此基礎上,進行升速實驗,實驗系統實物圖如圖8所示。
在24 000 r/min轉速時,加入IDOB的主動磁軸承系統與未加IDOB的主動磁軸承系統的位移波形對比如圖9所示。
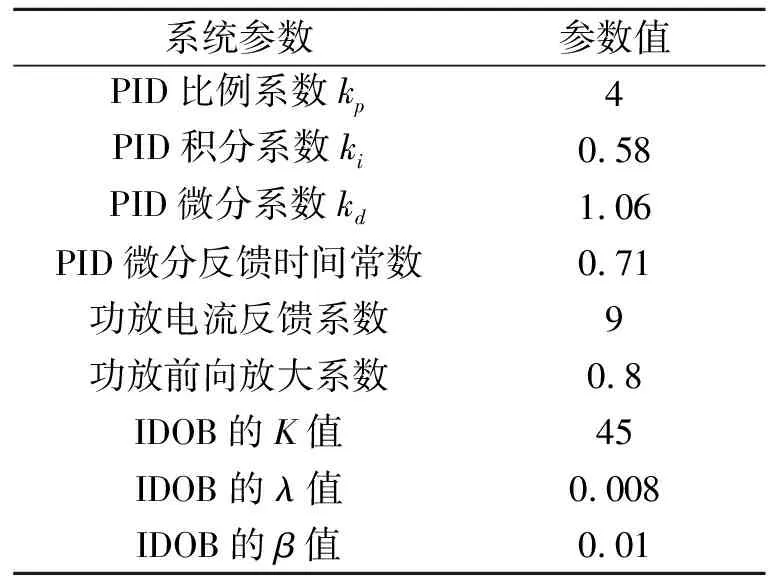
表3 100 kW磁懸浮電機磁軸承系統的徑向控制參數
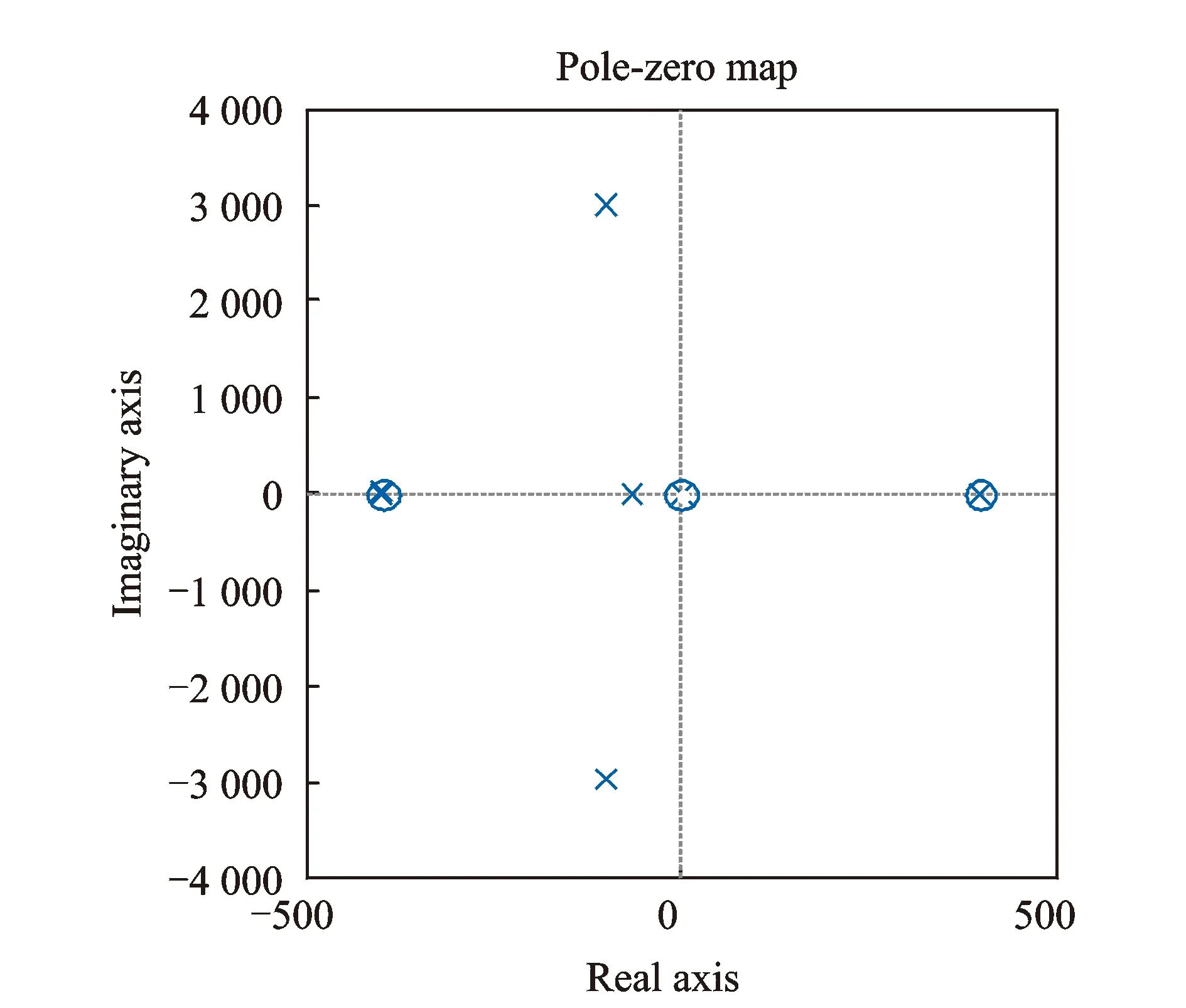
圖7 主動磁軸承轉子閉環(huán)系統零極點分布圖

圖8 100 kW磁懸浮電機實驗平臺
由圖9可以看出,原系統未加IDOB,主動磁軸承轉子在24 000 r/min轉速時低頻增益為-30 dB,徑向BY通道位移跳動量為57.6 μm,加IDOB的主動磁軸承系統在24 000 r/min轉速時低頻增益為-50 dB,徑向BY通道位移跳動量為20.8 μm,相比于原系統,加入IDOB的主動磁軸承系統低頻增益減小20 dB,位移跳動量減小36.8 μm,控制精度提高了63.89%。實驗結果表明,離散PID控制器加IDOB能很好地抑制主動磁軸承轉子在高速時的低頻振動,提高主動磁軸承轉子系統的穩(wěn)定性。
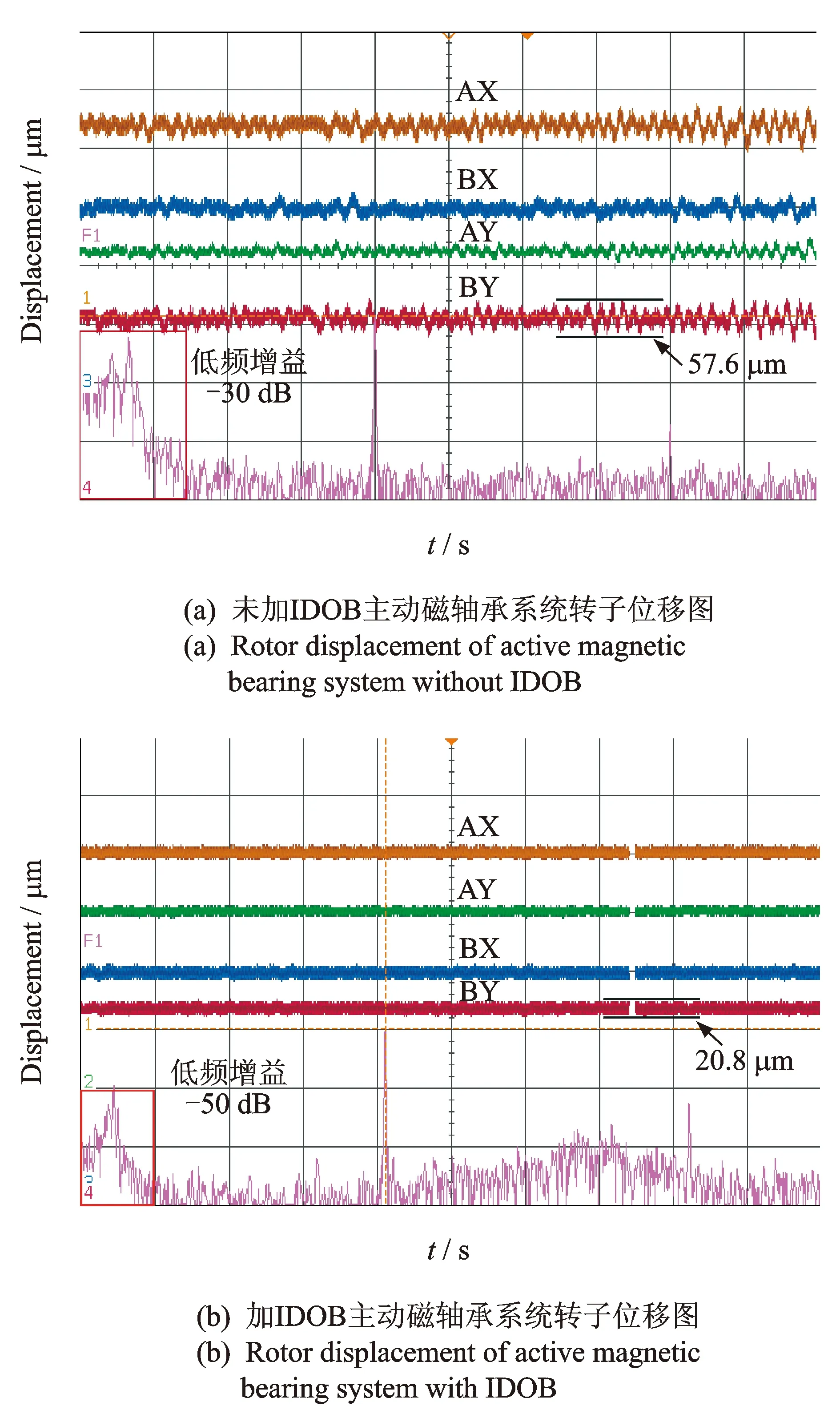
圖9 主動磁軸承轉子升速位移對比圖
5 結 論
本文針對磁懸浮電機轉子高速時低頻振動加劇,穩(wěn)定性變差的問題,提出利用改進型干擾觀測器——IDOB對低頻振動進行觀測,并在控制器中進行消除的方法,用來抑制磁懸浮電機轉子在高速時的低頻振動,提高磁懸浮電機轉子高速時的穩(wěn)定性。升速實驗結果表明,加入IDOB后的主動磁軸承系統相較于原系統,在24 000 r/min轉速時低頻增益減小20 dB,轉子跳動量減小36.8 μm,控制精度提高了63.89%,由此說明,IDOB的加入能很好抑制磁懸浮電機轉子高速時的低頻振動,改善其高頻特性,提高高速時的穩(wěn)定性。
參考文獻:
[1] 施韋策 G,布魯勒 H,特拉克斯勒 A.主動磁軸承基礎、性能及應用[M].虞烈,袁崇軍,譯.謝友柏,校.北京:新時代出版社,1997.Schweitzer G, Bleuler H, Traxler A. Basics, Properties and Applications of Active Magnetic Bearings[M]. Beijing: New Times Press, 1997.
[2] 謝振宇,牟偉興,周紅凱,等.基于轉速的磁懸浮軸承轉子系統變參數控制[J]. 振動工程學報,2012,25(6):739—744.XIE Zhenyu, MOU Weixing, ZHOU Hongkai, et al. Varying parameter control of active magnetic bearing rotor system based on rotation speed[J]. Journal of Vibration Engineering, 2012,25(6):739—744.
[3] 章琦,祝長生.電磁懸浮飛輪轉子系統的模態(tài)解耦控制[J].振動工程學報,2012,25(3):302—310.ZHANG Qi, ZHU Changsheng. Modal decoupling control for active magnetic bearing-supported flywheel[J]. Journal of Vibration Engineering, 2012,25(3):302—310.
[4] 鄭世強,房建成.MSCMG磁軸承μ綜合控制方法與實驗研究[J].儀器儀表學報,2010,31(6):1 375—1 380.Zheng Shiqiang, Fang Jiancheng. Experimental study on μ synthesis control for magnetic bearings of MSCMG[J]. Chinese Journal of Scientific Instrument, 2010,31(6):1 375—1 380.
[5] Fang Jiancheng, Zheng Shiqiang. AMB vibration control for structural resonance of double-gimbal control moment gyro with high-speed magnetically suspended rotor[J]. IEEE Asme Transactions on Mechatronics, 2013,18(1):32—43.
[6] 趙雪山.永磁偏置徑向軸向磁軸承H∞控制系統的研究[D].南京:南京航空航天大學,2004.Zhao Xueshan. Research on the H∞control system in the radial-axial magnetic bearing biased with permanent magnets[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2004.
[7] Alexander Smirnov, Rafal P Jastrzebski, Katja M Hynunen. Gain-scheduled and linear parameter-varying approaches in control of active magnetic bearings[A]. Proceedings of the 12thInternational Symposium on Magnetic Bearings[C]. Wuhan, China, 2010:350—360.
[8] Jugo J, Lizarrage I, Arredondo I. Nonlinear modeling and analysis of active magnetic bearing systems in the harmonic domain: a case study[J]. IET Control Theory Appl, 2008,2(1):61—71.
[9] Jugo J, Lizarrage I, Arredondo I. Nonlinear analysis of an AMB system using harmonic domain LTV models[A]. IEEE Int. Conf. Control Applications[C]. Munich, Germany, October 2006, 271—276.
[10] 王英,熊振華,丁漢.直線電機運動控制中的干擾觀測器的研究[J].中國機械工程,2004,15(17):1 549—1 552.WANG Ying, XIONG Zhenhua, DING Han. Research on disturbance observer for linear motion control[J]. China Mechanical Engineering, 2004,15(17):1 549—1 552.
[11] Umeno Takaji, Hori Yoichi. Robust speed control of dc servomotors using modern two degrees-of-freedom controller design[J]. IEEE Transactions on In-dustrial Electronics, 1991,38(5):363—368.
[12] Chen W H. Disturbance observer based control for nonlinear systems[J]. IEEE Trans. Mechatronics, 2004,9(4):706—710.

