極端頻率直接估計的新自適應陷波器方法

李 明， 涂亞慶， 沈廷鰲， 毛育文

(后勤工程學院信息工程系，重慶 401311)

引 言

振動工程中常見的極端頻率信號，其頻率估計精度具有很重要的理論意義和使用價值[1,2]。在離散頻譜校正理論中的極端頻率，主要相對于頻率分辨率而言(即采樣頻率和采樣時間長度的比值)，由于極端頻率頻譜泄露嚴重、存在柵欄效應和負頻率成分干涉，基于離散頻譜校正的頻率估計方法存在較大誤差[3,4]，且計算復雜，抗噪性較差，精度還有待進一步提高[5]，也無法估計時變信號的頻率值。

為改變此現狀，提高頻率估計方法的實時性、準確性和抗噪性，采用自適應陷波器(ANF)進行頻率估計。ANF主要是根據被處理信號的特點，對其進行參數優化，自動調節自身模型參數，令誤差函數達到最小值，使陷波頻率與信號頻率相等，從而估計出信號頻率值。每估計一次頻率值只需要3個采樣點，同離散頻譜校正理論中采樣時間長度的含義完全不同。該方法從時域角度進行迭代頻率估計，完全避免了負頻率成分的干擾，不存在頻譜泄露和柵欄效應問題，不僅可以估計頻率恒定的時不變信號，還可以估計頻率發生變化的時變信號；同時可以濾除信號噪聲，提高信噪比，針對噪聲環境下的弱信號也具有較好的檢測效果，且結構簡單、計算量小[6]。

由于ANF頻率估計方法同離散頻譜校正理論的差別較大，故本文所指的極端頻率信號，主要指歸一化頻率接近于0或π兩端的信號。例如，當采樣頻率設為4 096 Hz，型號為6307E型的滾動軸承，其內圈、外圈的故障特征頻率分別為76.5和98.8 Hz[7]，相對于采樣頻率4 096 Hz則為極低頻信號，其歸一化頻率接近于0。此外，當現有的采集裝置的采樣頻率限定為1 024 Hz時，旋轉機械轉子系統松動故障產生的10倍頻簡諧分量(基頻50 Hz，50×10 Hz=500 Hz，接近奈奎斯特頻率512 Hz)相對于采樣頻率1 024 Hz則為極高頻信號，其歸一化頻率接近于π。

針對上述信號進行頻率估計時，由于噪聲干擾增大，其頻率估計精度將出現明顯下降，且存在算法不穩定，收斂速度偏慢的缺點[8,9]。針對此問題，文獻[10,11]對ANF誤差函數進行了改進，使該誤差函數具備一定斜直線的特性，一定程度上加快了ANF收斂速度。文獻[12,13]針對上述文獻結果有偏的問題進行了研究，取得了近似無偏的頻率估計結果，但上述方法的缺點是最優頻率估計解為局部極小值點，對頻率初始值的設定有一定的要求，且為間接頻率估計，對估計后參數的取值有一定的限制；同時其頻率估計結果存在振蕩，針對極端頻率信號的估計精度和穩定性還有待進一步提升。

為此，本文為解決現有ANF方法估計極端頻率信號時存在收斂速度慢、精度不高、穩定性差的問題，通過提出一種新誤差函數，改善ANF在整個頻率范圍內的迭代收斂曲面，加快ANF收斂速度與算法穩定性；同時，采用偏差補償方式，降低噪聲對ANF的影響，提供近似無偏的極端頻率信號頻率估計結果。

綜上所述，本文提出了一種ANF極端頻率信號直接頻率估計新方法，并與原有算法進行了有關性能的比較分析。

1 極端頻率信號

設正弦信號為

(1)

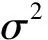
根據采樣定理，fs≥2f0，故可知信號頻率的取值范圍為0<ω0≤π；同時現有的ANF研究表明[14]，當信號頻率0<ω0≤0.1π或0.9π<ω0≤π時，ANF的性能出現明顯下降，所以本文討論的極頻信號主要指頻率0<ω0≤0.1π的極低頻信號或0.9π<ω0≤π的極高頻信號。

2 新自適應陷波器方法

2.1 新誤差函數

ANF傳遞函數為

(2)

式中ρ為極半徑，控制陷波寬度，且0?ρ<1。ANF參數a=-2cosω，ω為ANF陷波頻率，在頻率估計過程中，ω將趨近于ω0，故ω可看作為ω0的估計值，此時，a→a0=-2cosω0。

在頻率估計過程中，若估計a值，則為間接頻率估計，此時需保證-2≤a≤2，以使ω=arccos(-a/2)有解。但若估計ω，則為直接頻率估計，不需保證ω的取值范圍，步驟較為簡化。

為此，將a=-2cosω代入式(2)可得

(3)

式中N(z,ω)和H(z,ω)分別為ANF的FIR和IIR結構。則信號x(k)通過N(z,ω)和H(z,ω)的信號e1(k)和e2(k)分別為

(4)

為了獲得最佳頻率估計值，ANF通過調整陷波頻率ω，使下式的新誤差函數最小化

J(ω)=E[e2(k)(e1(k)+e2(k))]

(5)

式中E[·]表示求取期望，其保留了傳統IIR自適應陷波器頻率估計精度高，在最優頻率值附近下降速度快的優點；同時使誤差函數在遠離最優頻率值時仍能夠保持一定的梯度值，使其可保持較快的收斂速度。在實際計算中可按下式進行計算

(6)

由于輸入信號為正弦信號，故式(3)中N(z,ω)和H(z,ω)在輸入信號頻率ω0處的幅值為

(7)

相角為

(8)

結合式(4)，(7)和(8)，可得

(9)

將式(7)～(9)代入式(5)，可得

J(ω)=E[e2(k)(e1(k)+e2(k))]=

(10)

為說明所提新誤差函數的優越性，故比較文獻[10]所采用的如下式所示的原有誤差函數為

(11)

實際計算時按下式計算

(12)

為說明本文所提如式(5)所示新誤差函數的優越性，故所取參數同文獻[10]保持一致，A=1，θ=π/6，ρ=0.95，σ2=0，輸入信號頻率分別取3個不同的值，π/3，π/2和2π/3，則文獻[10]和本文方法所提誤差函數如圖1所示。又由于極高頻和極低頻具有對稱性，故只分析頻率ω0為0.01π時的極低頻信號，其他參數設置保持不變，則極端頻率下相應的誤差函數如圖2所示。

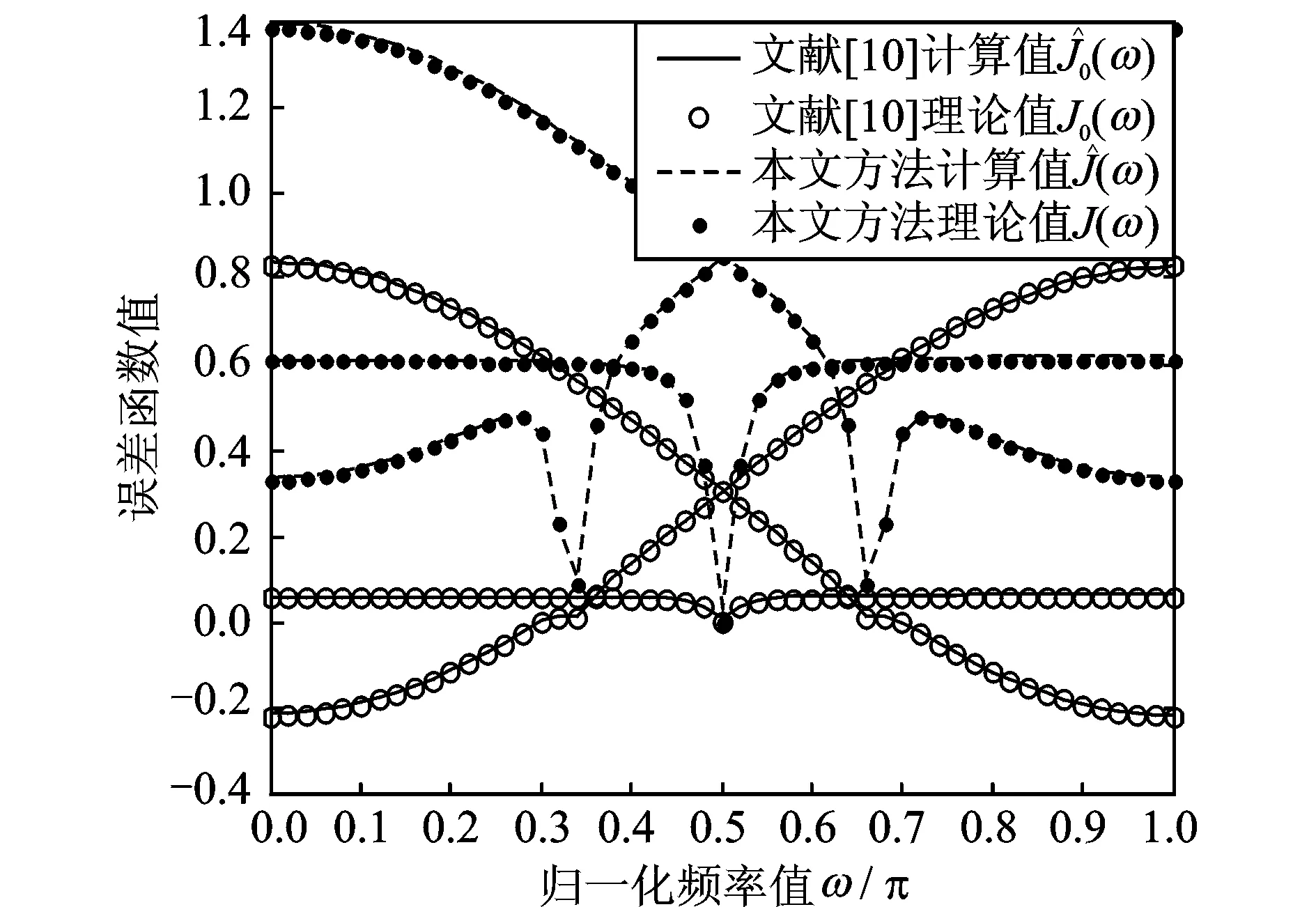
圖1 不同方法所提誤差函數的理論值與計算值

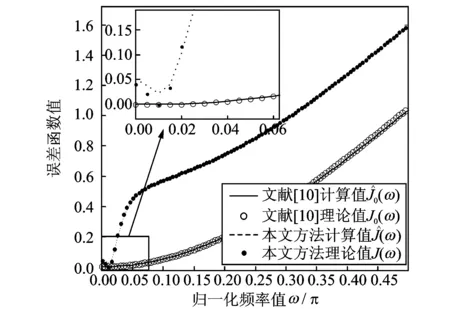
圖2 ω0=0.01π時不同方法所提誤差函數

由圖1，2可知，兩種不同誤差函數的理論計算值同實際計算值基本保持一致。同時，本文所提誤差函數J(ω)相較J0(ω)的梯度值較大，在迭代計算過程中的收斂速度將更快，且最優頻率值的選取較為明顯。特別當輸入信號頻率為極低頻，ω0=0.01π時，文獻[10]所提誤差函數在這一區域附近基本為平直線，喪失了對最優解的收斂性能，且容易在最優解附近產生收斂振蕩，導致其算法不穩定。而本文所提誤差函數仍然具有較大的梯度值，仍可收斂至最優頻率值，提升了算法的穩定性。

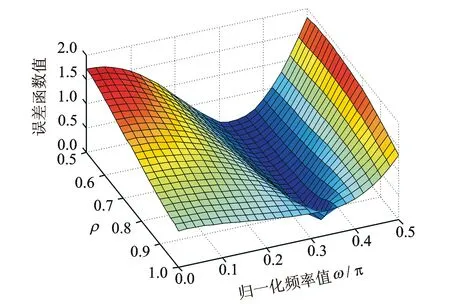
圖3 ω0=π/3時本文方法所提誤差函數曲面圖

圖4 ω0=π/3時原有誤差函數曲面圖

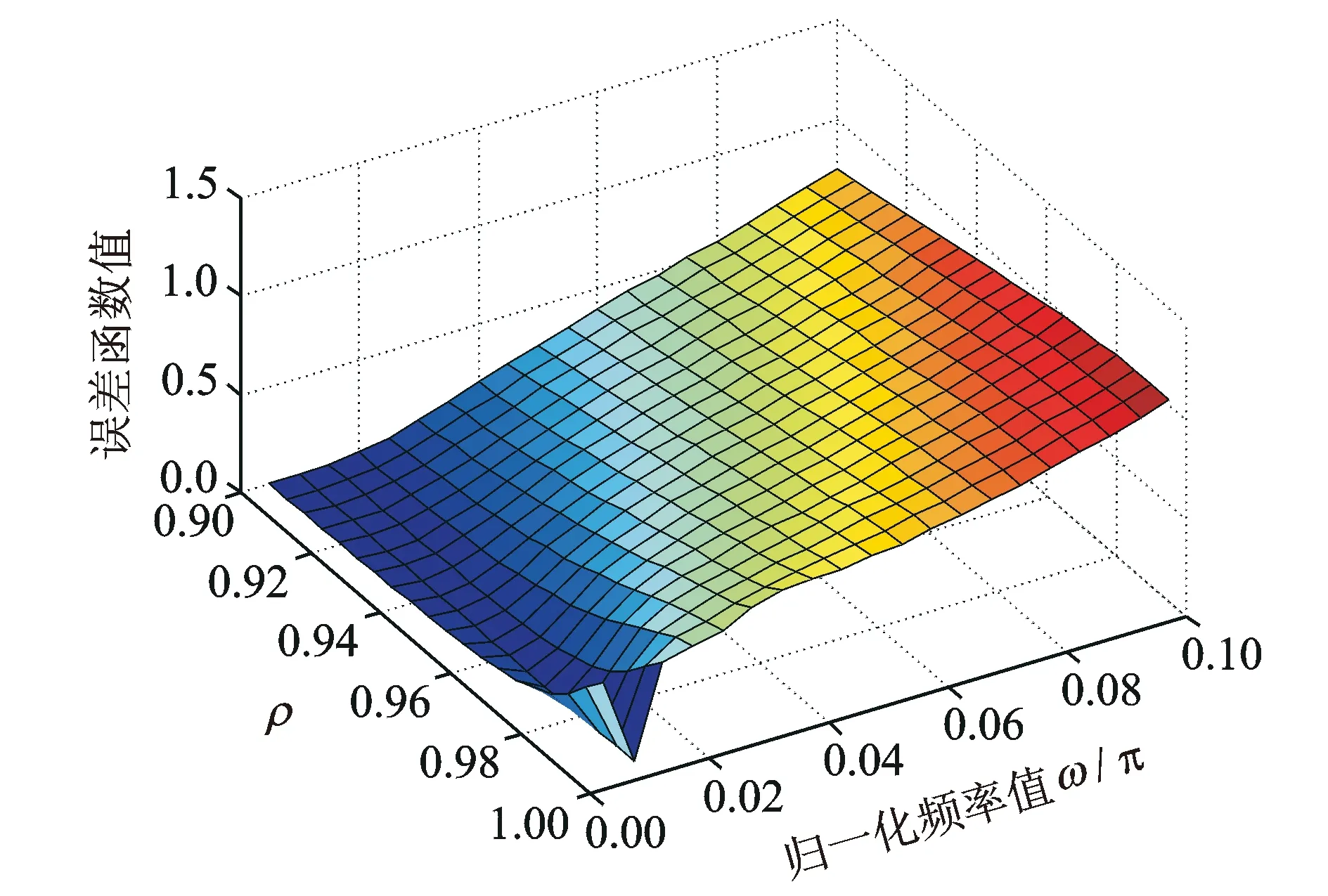
圖5 ω0=0.01π時本文方法所提誤差函數曲面圖

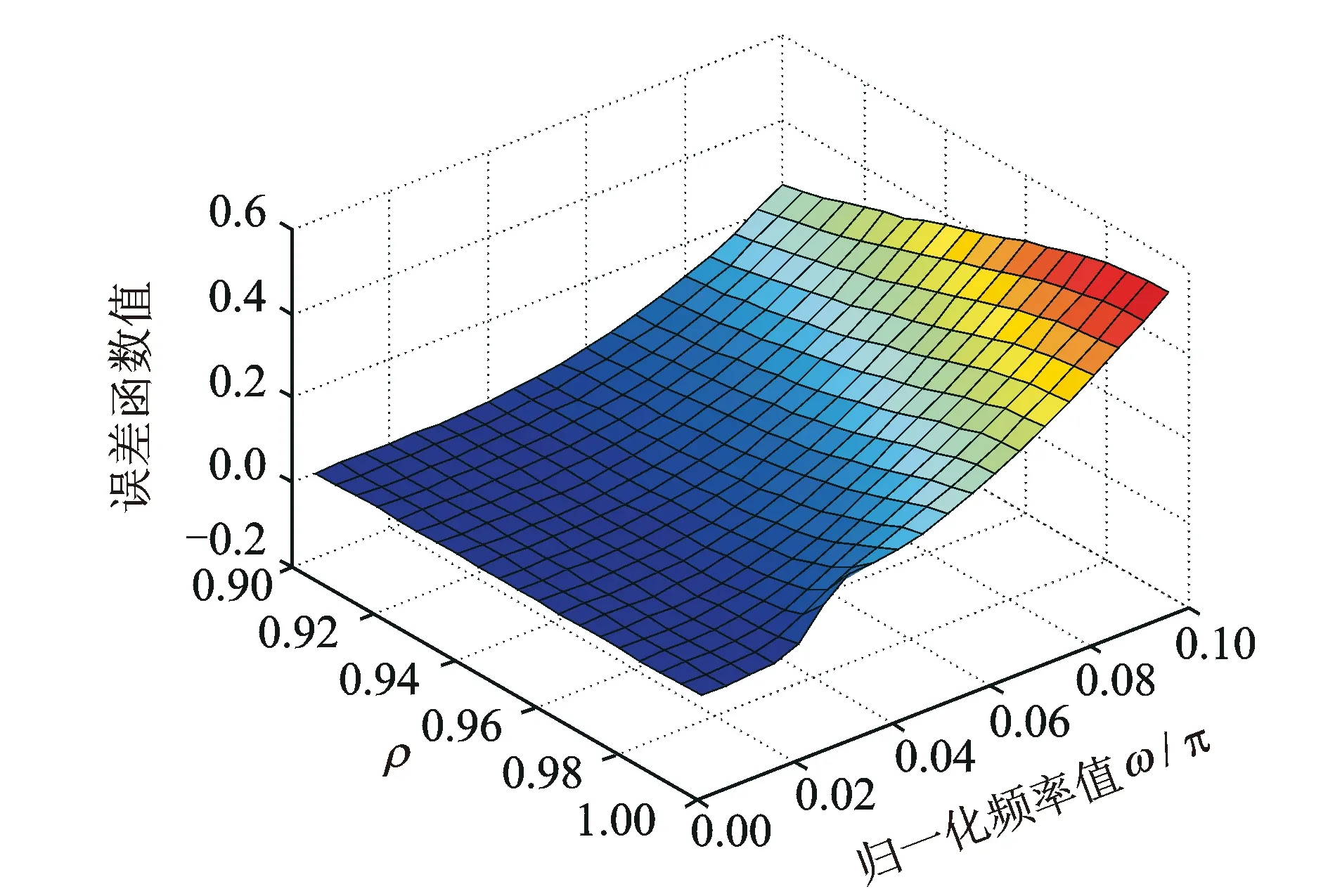
圖6 ω0=0.01π時原有誤差函數曲面圖

2.2 頻率估計偏差問題分析

結合式(5)所示新誤差函數，可知ANF直接頻率估計方法為

ω(k)-μ[(g1(k)+2g2(k))e2(k)+e1(k)g2(k)]

(13)

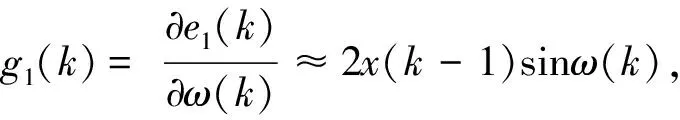
式(13)中的e1(k)g2(k)相對于其他項較小，為簡化計算，可略去e1(k)g2(k)[10]，于是可得

ω(k+1)=ω(k)-μ[g1(k)+2g2(k)]e2(k)

(14)

令

(15)

可知g1(k)和g2(k)分別為x(k)通過G1(z,ω)和G2(z,ω)后的信號。

一般而言，式(14)所示頻率估計方法結果有偏，為消除該偏差，對式(14)進行穩態條件下的偏差分析，此時ω→ω0，故可得[15]

(16)

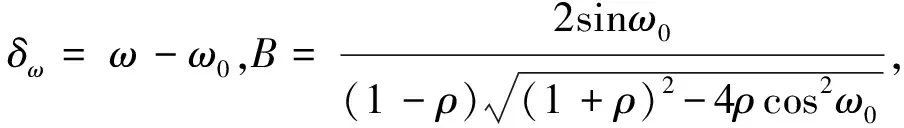
穩態下，由于ω→ω0，故可用ω0替代式(15)中的ω(k)，由此可得e1(k)，e2(k)，g1(k)和g2(k)的表達式

(17)

其中，δω(k)=ω(k)-ω0；v1(k)，v2(k)，v3(k)和v3(k)為噪聲v0(k)分別通過N(z,ω)，G1(z,ω)，H(z,ω)和G2(z,ω)后所產生。

由此，將式(14)的兩邊同時減去ω0，可得

δω(k+1)=δω(k)-μ[g1(k)+2g2(k)]e2(k)

(18)

對式(18)兩邊同取期望，并將式(17)代入。同時，令Ri,j=Rj,i=E[vi(k)vj(k)]表示噪聲vi(k)和vj(k)的相關值，計算時由于ρ→1，為簡化計算，設(1-ρ)2≈0，則可得

E[δω(k+1)]=E[δω(k)]-μE[g1(k)+2g2(k)]e2(k)=(1-μM1)E[δω(k)]+

(19)

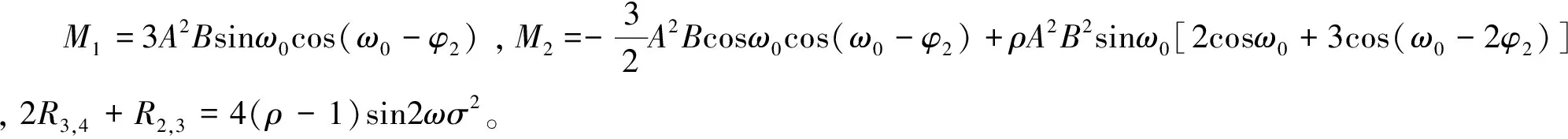
由式(19)可知，其右邊最后一項，即輸出信號間噪聲的相關性，是導致如式(14)所示頻率估計算法結果有偏的根本原因。同時，該項是輸入信號噪聲σ2、極半徑ρ和頻率估計結果ω的函數，且無論如何調整上述參數，都無法使該項為0。為此，需消除此項的影響，提高其頻率估計精度。

2.3 無偏頻率估計方法

為得到無偏頻率估計結果，需對輸入信號噪聲σ2進行估計。為此，令c(k)=4(ρ-1)sin2ω(k)，分析可知

E[c(k)x(k)e1(k)]=

c(k)A2sinω0cosφ1E[δω(k)]+c(k)σ2

(20)

式(20)中右邊最后一項包含了2R3,4+R2,3的值，于是，將式(20)中的c(k)x(k)e1(k)代入式(18)，兩邊同取期望。雖然引入了多余項c(k)A2sinω0cosφ1·E[δω(k)]，但是該項可與式(19)中的M1合并，對頻率估計精度的影響較小，由此可知基于新誤差函數的ANF極端頻率無偏直接估計新方法為

ω(k+1)=ω(k)-μG(k)

(21)

其中，G(k)=[g1(k)+2g2(k)]e2(k)-c(k)x(k)e1(k)。

該算法流程為：

Step1. 設置頻率初始值ω(0)，算法步長μ和ANF參數ρ；

Step2. 在k時刻，將信號x(k)分別通過N(z,ω)和H(z,ω)，得到e1(k)和e2(k)，并計算c(k)；e1(k)=x(k)-2cosω(k)x(k-1)+x(k-2),e2(k)=e1(k)+2ρcosω(k)e2(k-1)-ρ2e2(k-2),c(k)=4(ρ-1)sin2ω(k)。

Step3. 計算k時刻的信號g1(k)和g2(k)，同時計算G(k)的值；

G(k)=[g1(k)+2g2(k)]e2(k)-c(k)x(k)e1(k)

Step4. 按式(21)更新頻率估計值，得到

ω(k+1)=ω(k)-μG(k)

Step5. 重復步驟Step2～Step4，直至算法收斂。

3 性能分析

3.1 穩態偏差分析

對式(21)進行穩態條件下的偏差分析，式(21)兩邊同減去ω0并取期望，得

E[δω(k+1)]=E[δω(k)]-μE[G(k)]=

[1-μ(M1-c(k)A2sinω0cosφ1)]E[δω(k)]+

(22)

穩態條件下，可知

(23)

式(22)可變化為

(24)

3.2 穩態MSE分析

對式(21)兩邊同減去ω0并平方，求取期望可得

(25)

式(25)左邊第二項的計算可利用文獻[13]所用方法，得

2μE[G(k)δω(k)]=2μE[δω(k-2)G(k)]-

(26)

則結合式(26)，將式(25)展開，經過一系列復雜繁瑣的推導后，可得

(27)

其中，ψ1=A2sinω0[6Bcos(ω0-φ2)-2ccosφ1]，ψ2=A4sin2ω0[9B2+9B2cos(2φ2-2ω0)/2-

3cBcos(φ1-φ2-ω0)-6cBcos(φ2-ω0)cosφ1]，

2cos2(iω0)]+6Bc[cos(φ1-φ2-ω0)cos(2iω0)+

2cos(ω0-φ2)cosφ1]}，ψ4=4sin2ω0(1-ρ)(13-32cos2ω0)σ4。

結合式(23)可知，穩態下式(27)可化為

(28)

4 計算驗證

4.1 頻率估計精度分析

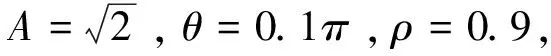
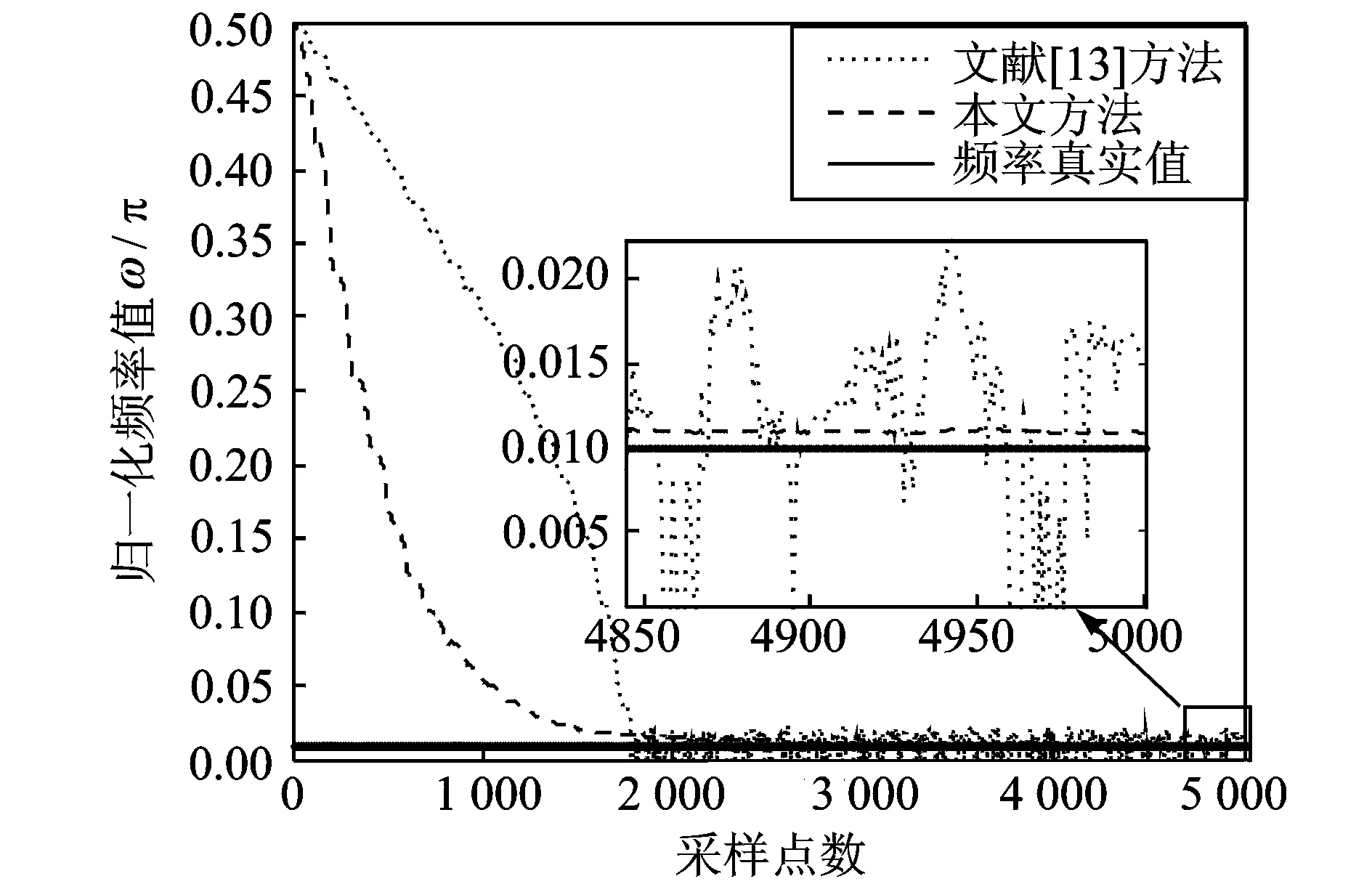
圖7 ω0=0.01π時ANF頻率估計效果圖

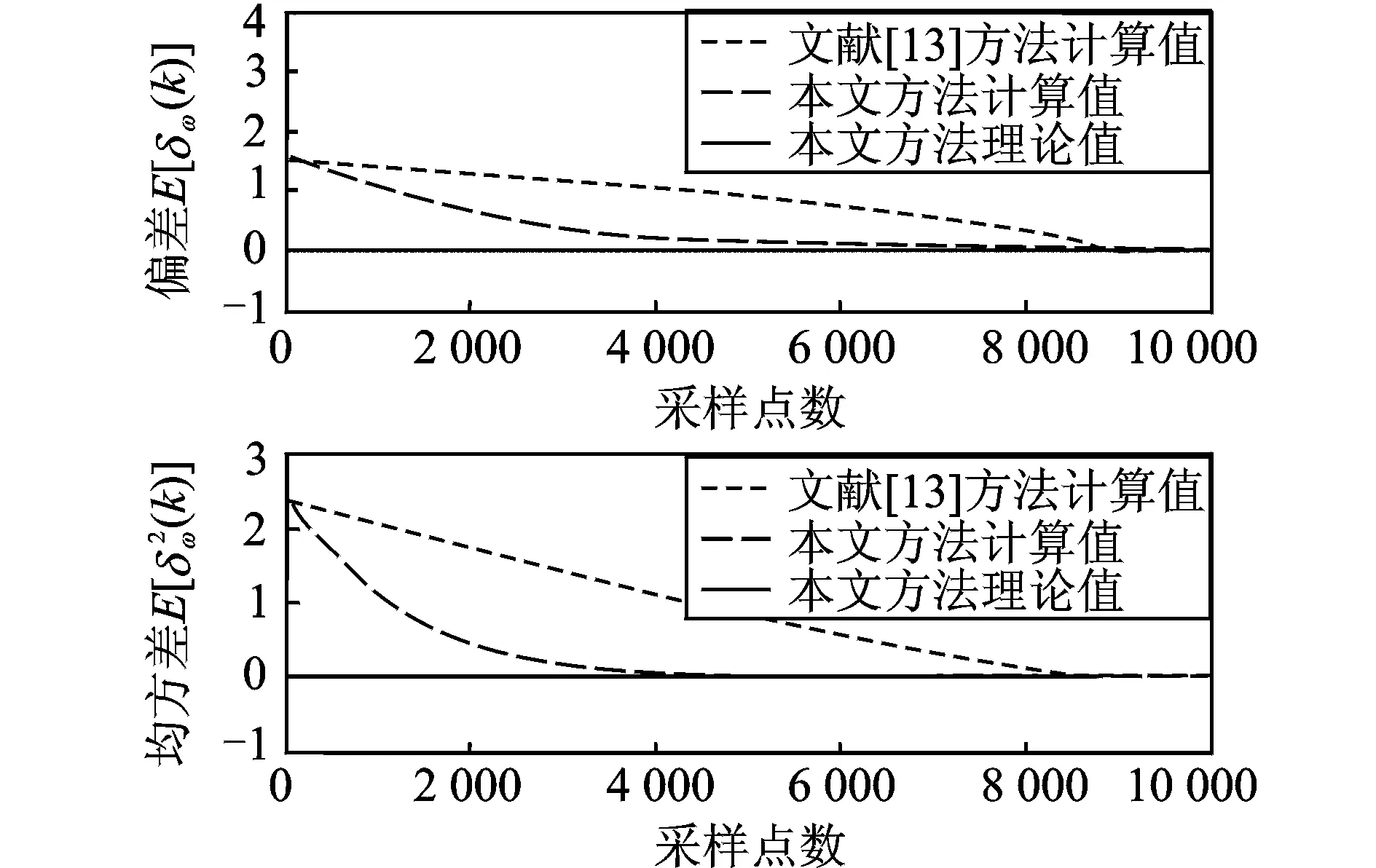
圖8 ANF頻率估計偏差E[δω(k)]和均方差

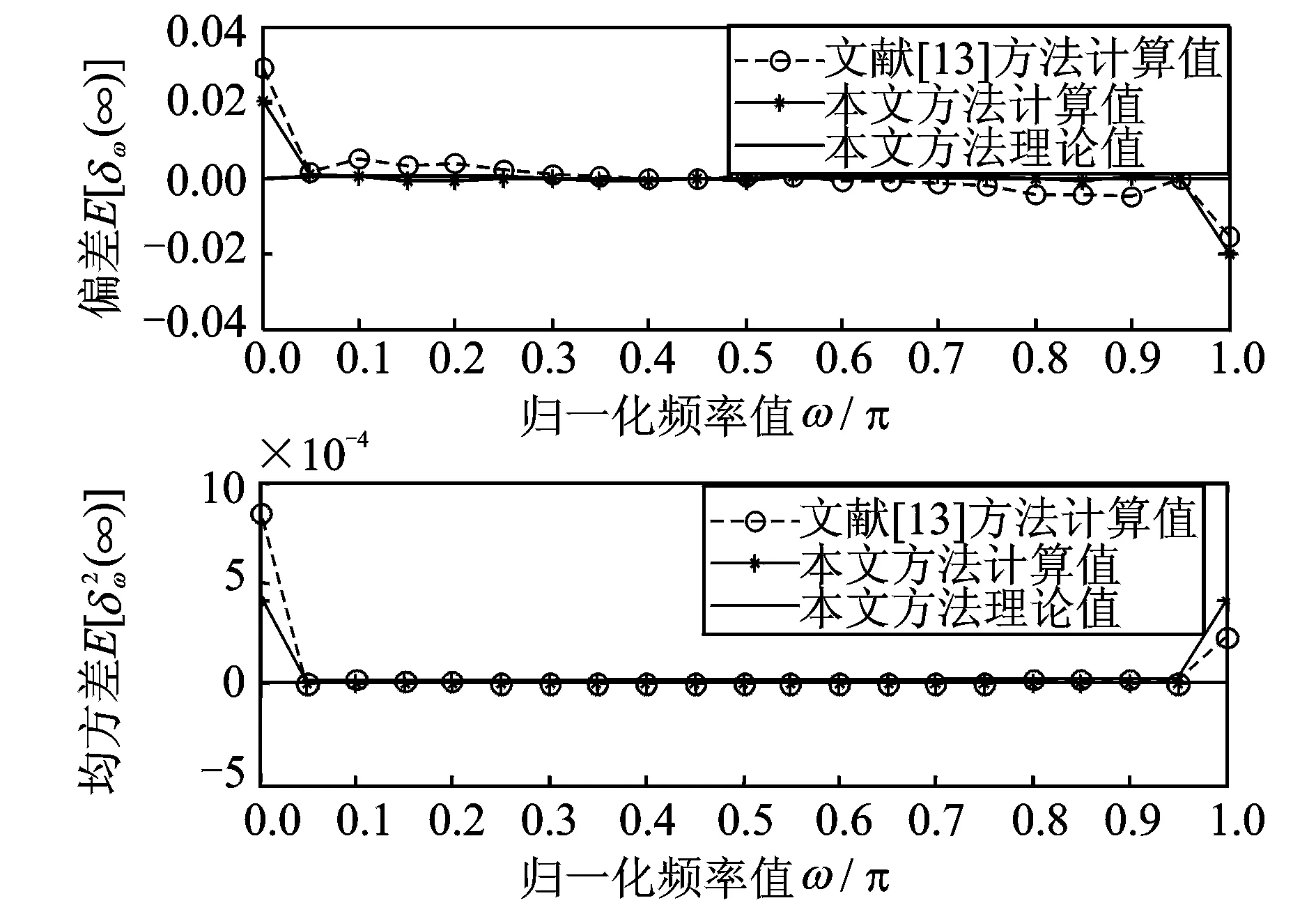
圖9 ANF在全頻段頻率估計偏差E[δω(∞)]和均方差

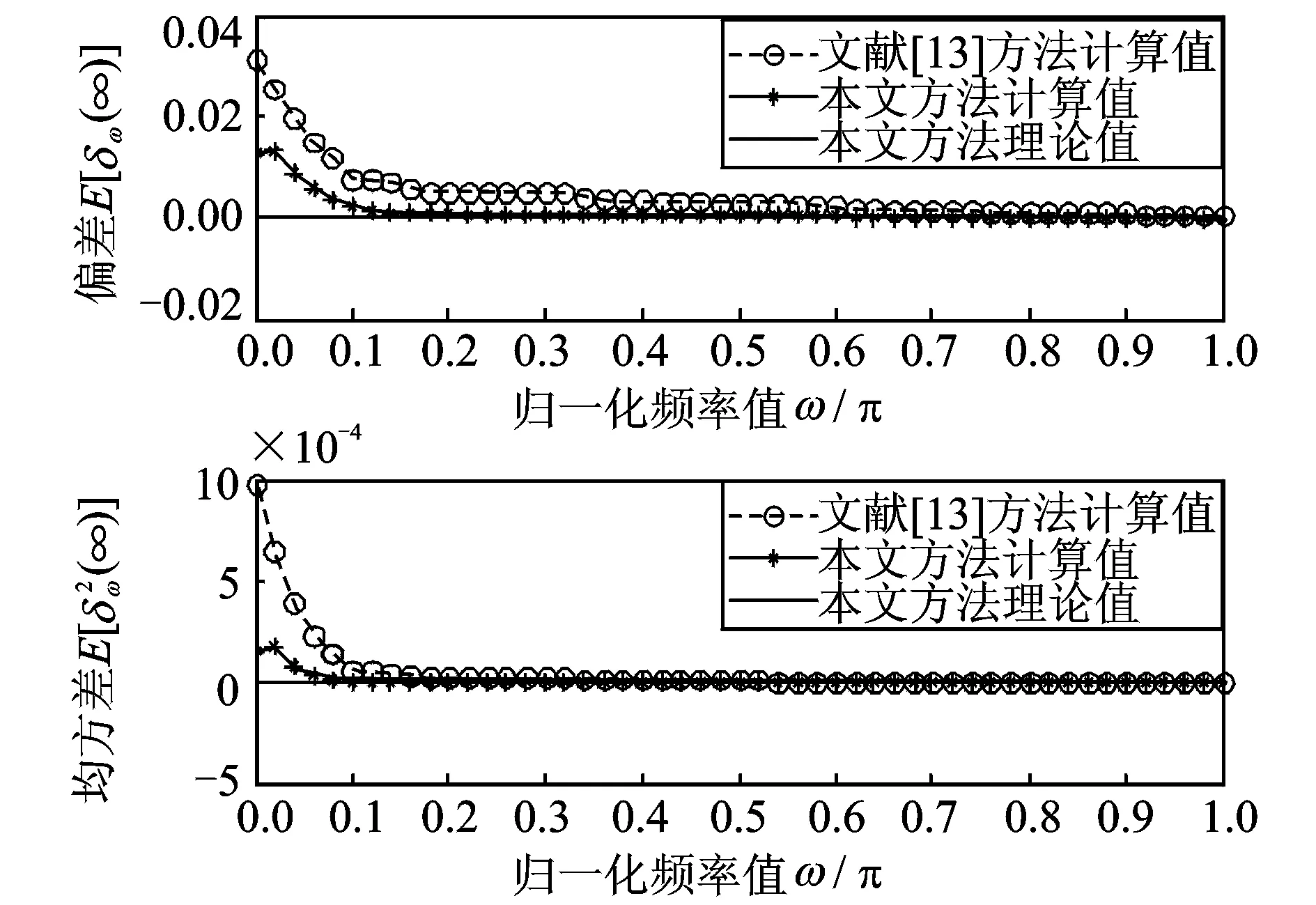
圖10 SNR=5 dB時ANF在0<ω0≤0.1π的頻率估計偏差E[δω(∞)]和均方差

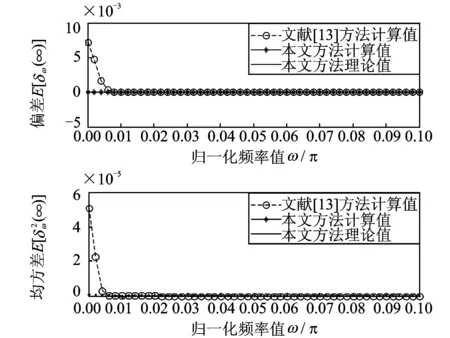
圖11 無噪聲時ANF在0<ω0≤0.1π的頻率估計E[δω(∞)]和

4.2 時變信號頻率估計精度分析

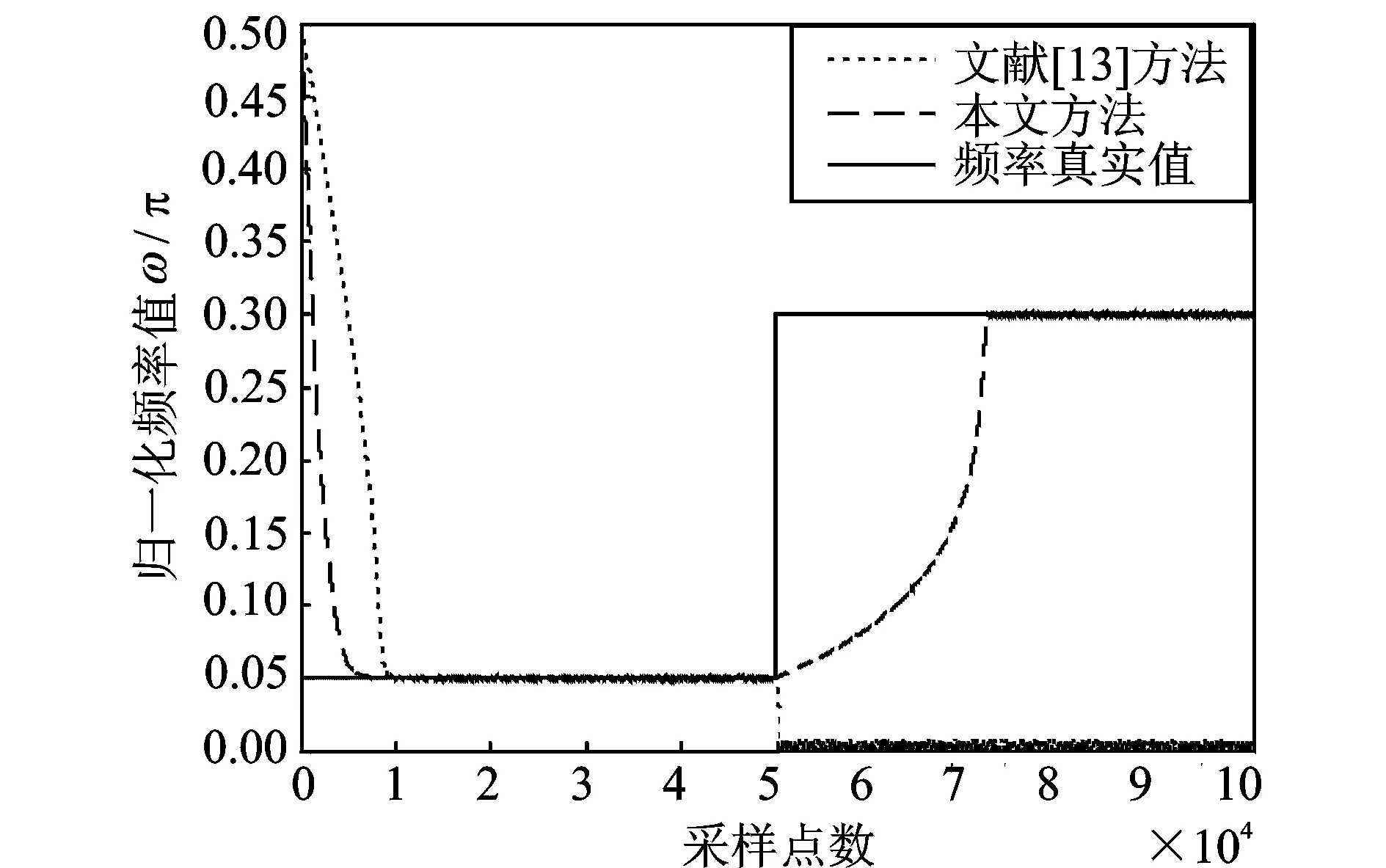
圖12 ANF時變信號頻率估計效果圖

保持參數設置不變，待估頻率值ω0開始設為0.05π，在第5×104個采樣點后變為0.3π。則ANF估計時變信號頻率的效果如圖12所示。由圖12可知，本文方法能夠較好地跟蹤時變信號，但文獻[13]所提方法在信號頻率由0.05π變為0.3π時，喪失了跟蹤信號頻率的能力，這主要是由于當頻率發生變化時，誤差函數曲面也發生了變化，此時ANF的頻率估計值剛好位于變化后誤差函數的全局極小值點，而最優頻率解恰恰位于遠離此處的局部極小值點，從而導致其無法收斂至最優頻率解，反而繼續收斂至全局極小值點，導致頻率估計產生偏差，無法實時跟蹤時變信號的頻率。

4.3 步長μ對頻率估計精度的影響分析

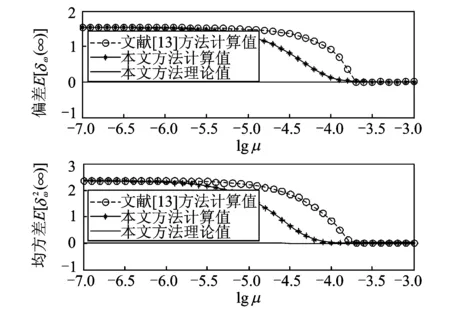
圖13 不同μ值下的ANF頻率估計偏差E[δω(∞)]和均方差

4.4 極半徑ρ對頻率估計精度的影響分析

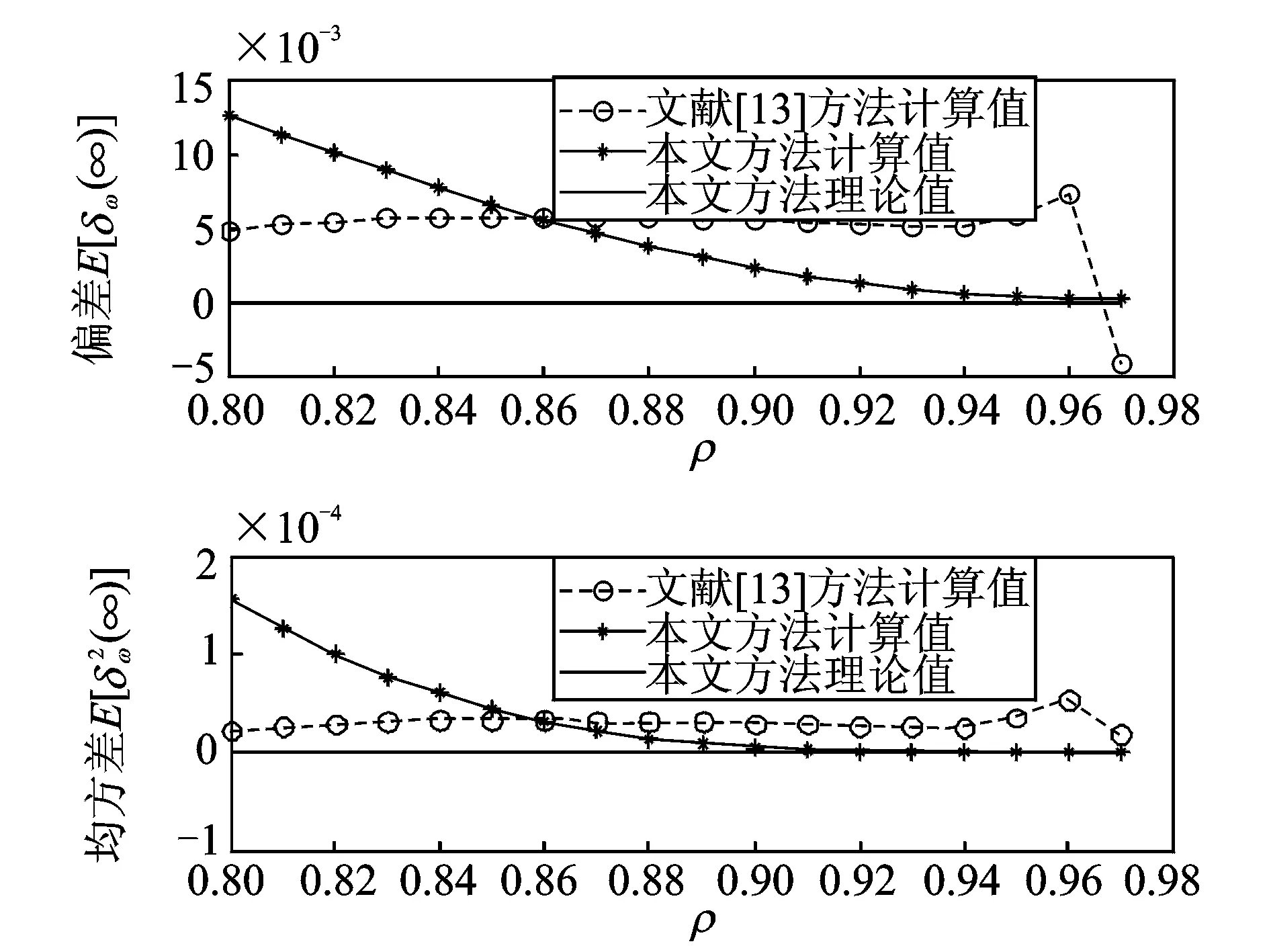
圖14 不同ρ值下的ANF頻率估計偏差E[δω(∞)]和均方差

4.5 不同信噪比(SNR)對頻率估計精度的影響分析

保持參數設置不變，圖15是不同信噪比下ANF的頻率估計精度。由圖15可知，當信噪比較高時，本文方法與文獻[13]方法的頻率估計精度相當，而當信噪比較低時，本文方法明顯優于文獻[13]方法。

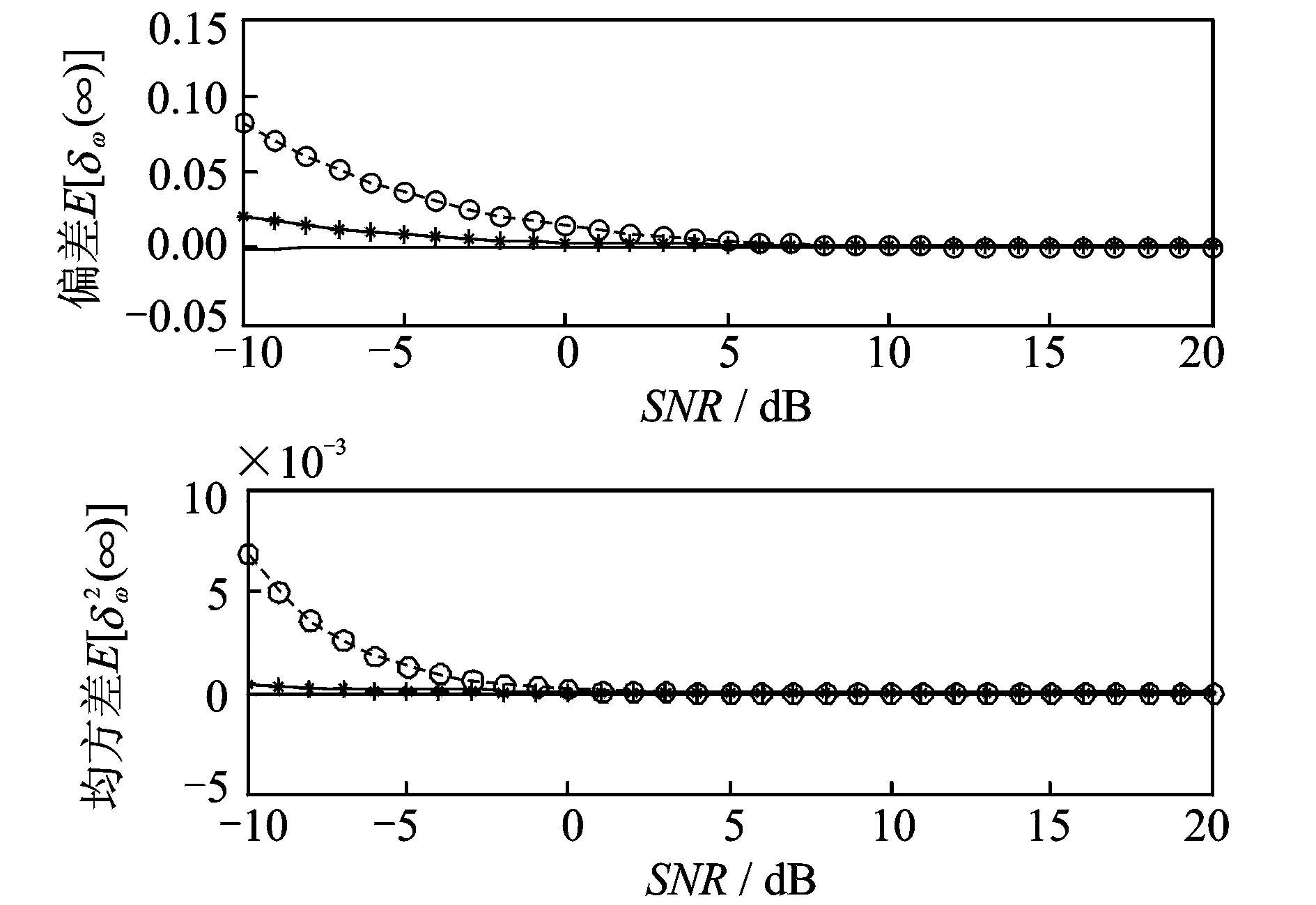
圖15 不同信噪比下的ANF頻率估計偏差E[δω(∞)]和均方差

5 結 論

針對ANF極端頻率估計存在的問題，提出了一種極端頻率估計ANF新方法。通過新誤差函數，改善ANF在整個頻率范圍內的迭代收斂曲面，加快了ANF收斂速度，增強了ANF頻率估計的穩定性；通過噪聲σ2估計，利用偏差補償技術，有效降低了ANF頻率估計的偏差與均方差，提高了頻率估計精度，獲得了近似無偏頻率估計結果；分析了所提方法的穩態性能。本文方法彌補了ANF對極端頻率信號進行頻率估計時的缺陷，拓展了ANF進行頻率估計的適用范圍。研究表明有如下結論：

(1) 算法精度較高。特別針對極端頻率信號時，較原方法有明顯提高。

(2) 算法抗噪性較好。在信噪比為-10～20 dB時，本文方法的頻率估計精度變化較原方法更小，且MSE值基本保持不變。

(3) 算法實現簡單。本文算法相對于原算法增加的計算量較少，且為時域遞推算法，實時性可以得到滿足。

參考文獻：

[1] 毛育文，涂亞慶，張海濤，等. 極低頻信號的一種離散頻譜校正新方法[J]. 振動工程學報，2012，25(4)：474—480.Mao Yuwen, Tu Yaqing, Zhang Haitao, et al. A discrete spectrum correction method for ultra low frequency signals [J]. Journal of Vibration Engineering, 2012, 25(4): 474—480.

[2] 毛育文，涂亞慶，張海濤，等. 計及負頻率的極高頻信號離散頻譜校正新方法[J].振動、測試與診斷，2012，32(3)：477— 482.Mao Yuwen, Tu Yaqing, Zhang Haitao, et al. New discrete spectrum correction method with negative frequency contribution for ultra high frequency signals[J]. Journal of Vibration , Measurement & Diagnosis, 2012, 32(3): 477—482.

[3] 陳奎孚, 王建立, 張森文. 頻譜校正的復比值法[J]. 振動工程學報,2008,21(3) :314—318.Chen Kuifu, Wang Jianli, Zhang Senwen. Spectrum correction based on the complex ratio of discrete spectrum around the main-lobe [J]. Journal of Vibration Engineering, 2008, 21(3): 314—318.

[4] 楊志堅, 丁康. 調制FFT 及其在離散頻譜校正技術中的應用[J] .振動工程學報, 2009,22(6): 623—637.Yang Zhijian, Ding Kang. Modulated FFT and its application in the discrete spectrum correction[J]. Journal of Vibration Engineering, 2009, 22(6): 623—637.

[5] 毛育文，涂亞慶，肖瑋，等. 離散密集頻譜細化分析與校正方法研究進展[J]. 振動與沖擊, 2012, 31(21): 112—119.Mao Yuwen, Tu Yaqing, Xiao Wei, et al. New discrete spectrum correction method with negative frequency contribution for ultra high frequency signals [J]. Journal of Vibration and Shock, 2012, 31(21)：112— 119.

[6] Prioakis J G, Manolakis D G. Digital Signal Processing: Principle, Algorithms, and Application [M]. New Jersey: Prentice Hall, 2006: 112—114.

[7] 陳向民，于德介，羅潔思. 基于信號共振稀疏分解的包絡解調方法及其在軸承故障診斷中的應用[J]. 振動工程學報， 2012, 25(6): 628—636.Chen Xiangmin, Yu Dejie, Luo Jiesi. Envelope demodulation method based on resonance-based sparse signal decomposition and its application in roller bearing fault diagnosis [J]. Journal of Vibration Engineering, 2012, 25(6): 628—636.

[8] Johansson A T, White P R. Instantaneous frequency estimation at low signal-to noise ratios using time-varying notch filters [J]. Signal Processing, 2008, 88(5): 1 271—1 288.

[9] Minh T, Victor D B. Robust notch filtering by combining adaptation in both time and frequency [A]. Conference Record of the Forty-First Asilomar Conference on Signals, Systems and Computers[C]． 2007: 1 633—1 637.

[10] Punchalard R, Lorsawatsiri A, Koseeyaporn J, et al. Adaptive IIR notch filters based on new error criteria[J].Signal Processing, 2008, 88 (3):685—703.

[11] Punchalard R, Koseeyaporn J, Wardkein P. Adaptive IIR notch filter using a modified sign algorithm [J]. Signal Processing, 2009, 89(2):239—243.

[12] Loetwassana W, Punchalard R, Koseeyaporn J, et al. Unbiased plain gradient algorithm for a second-order adaptive IIR notch filter with constrained poles and zeros [J]. Signal Processing, 2010, 90(8): 2 513—2 520.

[13] Punchalard R. Mean square error analysis of unbiased modified plain gradient algorithm for second-order adaptive IIR notch filter [J]. Signal Processing, 2012, 92(11): 2 815—2 820.

[14] Minh T, Hieu T, Victor D B. Stochastic search methods to improve the convergence of adaptive notch filters[A]. IEEE 13th 2009 Digital Signal Processing Workshop and 5th IEEE Signal Processing Education Workshop[C]． DSP/SPE 2009,2009: 78—83．

[15] Zhou J, Li G. Plain gradient-based direct frequency estimation using second-order constrained adaptive IIR notch filter [J]. Electronics Letters, 2004, 40(5):351—352.