例談培養學生創新素質的操作策略

曹興軍

《全日制義務教育數學課程標準（2011年版）》指出：數學教育既要使學生掌握現代生活和學習中所需要的數學知識與技能，更要發揮數學在培養人的思維能力和創新能力方面不可替代的作用。培養小學生的數學創新意識，不僅有利于提高學生的數學素養，優化學生的思維方式，增強學生有效分析和解決問題以及創新的能力，而且對于學生形成科學的世界觀和實事求是的態度具有重要的影響。因此，在平時的課堂教學中，教師要善于創造環境、捕捉機會，努力培養學生的創新意識和能力。

一、創設教學情境，引導學生發現和提出問題

【案例1】“三角形的內角和”教學片段。

師：（課件出示正方形）在數學中，我們將正方形的四個角叫做它的內角，正方形的內角和是多少度呢？（板書：內角和）

師：現在老師將這個正方形沿著對角線剪開（課件演示），變成了兩個完全相同的直角三角形。

師：三角形有幾個角？這節課，我們就來研究三角形的內角和。（板書課題）

師：（課件出示一個直角三角形）這個直角三角形的內角和是多少度呢？

師：把一個長方形沿對角線剪開，會怎樣？（課件演示）這個直角三角形的內角和是多少度？

師：通過剛才的研究，同學們有什么發現？

生：是不是所有的直角三角形其內角和都是180度？

（師生交流。）

小結：所有直角三角形的內角和都可以看做長方形的一半，是180度。

師：通過剛才的研究，同學們還能提出和我們今天要研究的內容有關的數學問題嗎？

生：銳角三角形、鈍角三角形的內角和是多少度？

師：（揭示課題）今天這節課我們一起來研究三角形的內角和。（板書課題）

這里，教師巧妙地創設出一個特殊的數學情境：直角三角形的內角和，以此引發學生深度思考。通過交流，學生發現和提出了新的有價值的數學問題，也就是本課要研究的重點問題。教學中教師營造了良好的、寬松的課堂氛圍，讓每個學生都敢于提問，為學生的創新意識和能力的培養打下良好的基礎。

二、善用引導啟發，培養學生獨立思考的能力

【案例2】“解決問題的策略——轉化”教學片段。

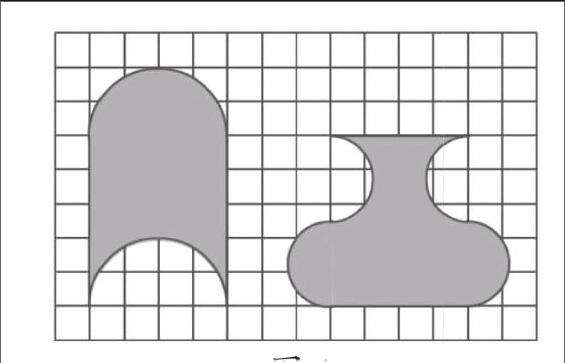
提問：（出示圖形，如圖1）這兩個圖形的面積相等嗎？

引導：這兩個圖形規則嗎？能不能想辦法“變”成我們熟悉的圖形呢？

操作：請同學們在練習紙上分一分、畫一畫。

提問：先看第一幅圖，誰來說說你是怎么想的。

（多媒體動態演示圖形的平移和轉化過程。）

引導：這兩幅圖原來怪怪的。經過平移或旋轉，都轉化成了什么圖形？

交流：現在能比較它們的面積相等嗎？

生：相等。

引導：這里的相等，是我們借助了一種很重要的策略得到的，是什么策略呢？

生：轉化。

提問：轉化以后，圖形的什么沒有變？

生：面積。

引導：面積沒變，干嗎還要轉化？

學生自由說：原來圖形不規則，不容易比較……

小結：轉化后，我們就把復雜的不規則的圖形轉化成了簡單的規則圖形。

這里，教師通過問題情境，啟發引導學生獨立思考，讓學生意識到用轉化的策略將復雜的不規則的圖形轉化成簡單的規則圖形，體會轉化策略的優點，把握了問題的本質。學生自主意識得到增強，獨立思考的能力得到提升，創造性解決問題的能力得到提高。

三、巧抓課堂生成資源，培養學生想象力和好奇心

【案例3】“長方形的周長”教學片段。

出示一道習題：“王爺爺家用籬笆圍一個長10米、寬6米的長方形雞圈，需要籬笆多少米？”

生1：（10+6）×2=32（米）。

師：還有不同的方法嗎？

生2：10×2+6×2=32（米）。

生3：如果雞圈有一面靠墻，就不需要這么多籬笆了。

師：能夠聯系實踐思考問題，很好。

生4：也有可能兩面靠墻。

師：同學們考慮得很全面。一面靠墻或者兩面靠墻需要籬笆多少米呢？我們可以借助什么思考？

生5：畫圖。

師：下面請同學們小組合作，畫出示意圖，列出相應的算式解答。

就這道習題而言，面對課堂教學中學生這種突然出現的回答，教師沒有打斷學生的思考，及時有效地利用這一生成資源，培養學生的想象力和好奇心，使學生在新知學習中不斷提高認識，有效構建新的知識體系，領悟方法，發展思維，實現創新。

四、經歷猜想、驗證，體驗知識的再創造過程

【案例4】“比的基本性質”教學片段。

1.問題引入。

問題1：回憶除法的商不變性質和分數的基本性質。

問題2：說說比同除法、分數的關系。

問題3：求出3∶4、6∶8、9∶12三個比的比值，得出3∶4=6∶8=9∶12。

提問：觀察、分析“3∶4=6∶8=9∶12”前項、后項的變化，有什么發現？

生：比的前項、后項同時乘2或3，比值不變。

2.引發猜想。

引導學生思考：根據剛才的發現，聯系分數的基本性質和除法商不變的性質，想一想：兩個比值相等的比之間有怎樣的性質和規律？

學生交流匯報，形成猜想：比的前項和后項同時乘或除以一個相同的數，比值不變。

3.驗證規律。

提問：是不是所有的比都有這樣的變化規律？你能想辦法驗證嗎？

學生驗證后，交流各自的想法。

生1：根據比與除法、分數的關系，認為比應該有類似的性質。

生2：把比寫成分數的形式，根據分數的基本性質發現比確實有這一規律。

生3：應用剛才的猜想舉例，然后求出兩個比的比值，發現猜想是正確的。

生4：將比寫成除法的形式，根據除法商不變的性質推導出比確實有這樣的性質。

4.總結提升。

師：誰能用一句話概括比的基本性質？“相同的數”是不是什么數都可以？為什么？

總結：比的前項和后項同時乘或除以相同的數（0除外），比值不變。

在整個活動中，教師引導學生從不同角度來探索，經歷“先猜想，后驗證”，將觀察、分析、假設、驗證交織在一起，體驗知識的再創造過程，不斷提高學生發現問題、提出問題和解決問題的能力。并能根據條件合理作出猜想，培養思維的創造性。在這樣的數學活動中，學生不僅獲得了知識與技能，而且創新意識和能力也得到了提高。

總之，學生自己發現和提出問題是創新的基礎；善于獨立思考是創新的核心；歸納概括得到猜想和規律，并加以驗證，是創新的重要方法。學生創新意識和能力的培養應該從課堂的點滴做起，為學生創設發現并提出問題的情境，善用課堂中能夠培養學生想象力和好奇心的生成資源，引導啟發學生獨立思考，經歷知識再創造的過程，促進學生創新意識和能力的全面提升。

（責編 黃春香）endprint