Mathematica繪圖在微積分教學中的應用

賈屹峰 鄭紅芬 王志高

（中國勞動關系學院基礎部，中國 北京 100045）

0 引言

在微積分教學中，描繪函數的圖像必不可少，例如一元微積分中數列的極限、函數的間斷點、曲線的凹凸性、函數的極值、拐點、拐點，二元函數的圖像、多重積分的積分區域等。函數的圖像在體現數學的美的同時，更重要的是使得許多重要的數學概念有了直觀的表示，使得這些概念更容易理解。

利用傳統的描點法繪圖，不僅浪費時間，而且只能畫出草圖，即缺乏精確性，又不夠直觀。應用Mathematiea軟件，可以利用簡單的命令，不但能夠在短時間內畫出更直觀、準確的圖像，而且能以動畫的形式演示。同時能夠激發學生的學習興趣，使得學生對相關的數學概念有更直觀、更深刻的了解，加深對知識的理解、記憶和深化，達到好的教學效果。

1 Mathematica基本繪圖函數

Mathematica具有很強的繪圖能力，用戶只需調用繪圖函數，即可很方便地畫出一元函數和二元函數在所需范圍內的平面圖像與三維圖形，并可以在同一坐標系內以不同的顏色顯示，進行比較。Mathematica基本繪圖函數有：

2 Mathmatica繪圖功能的應用

2.1 在一元微積分教學中的應用

極限是微積分最基本的概念，也是微積分教學中的難點

實例1 在很多的《微積分》教材中，割圓術是引入極限定義的經典例題，利用Mathematica可以很容易繪制出割圓術的圖形：

實例2 為了進一步給出數列極限的定義，通常是在實例1的基礎上，觀察下面三個數列的變化趨勢，利用下面的命令，可以畫出三個數列的圖像。

在教學過程中，讓學生觀察實例1與實例2的所畫出的圖像，給學生一個直觀的印象，在此基礎上，逐步引入極限的ε-N？定義，使學生更容易理解極限的定義。同樣，在講述第二個重要的極限時，也同樣利用畫圖和數值計算，并結合該極限的一個應用實例：存款利率，使得學生對自然對數的基底e有著更為深刻的理解，并對以后研究函數y=ex的性質打下基礎。

函數的連續性以及各種間斷點，是微積分一個重要的知識點，在教學過程中，通過對于函數圖像的觀察，特別是震蕩間斷點，使得學生對于極限與連續的關系，以及各類間斷首先有一個直觀的印象，然后再進一步的學習，例如，利用下面的命令，

圖1

圖2

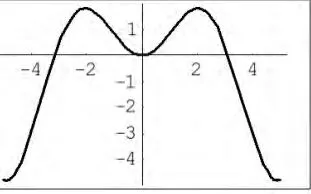
圖3

通過觀察上述函數的圖像，并加以比較，對學生理解極限與連續的關系和各類間斷點有很大的幫助。

在導數應用的教學過程中，在求出函數的單調性、凹凸性、極值點、拐點和漸近線等的基礎上，通常要畫出函數的圖像，這時如果利用Mathematica就能很容易畫出函數的圖像。

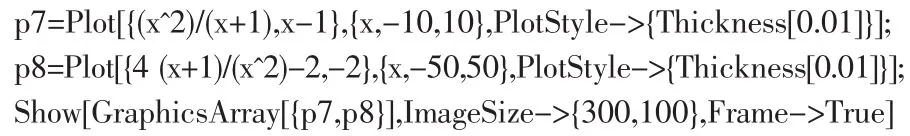
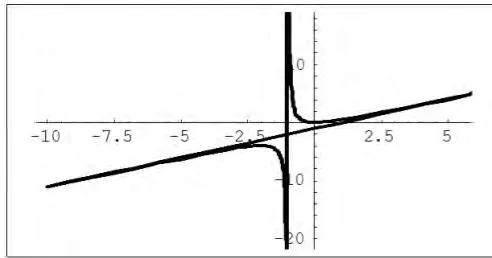
圖4

圖5

在定積分的應用中，積分上下限的確定通常需要實際問題畫出圖像。

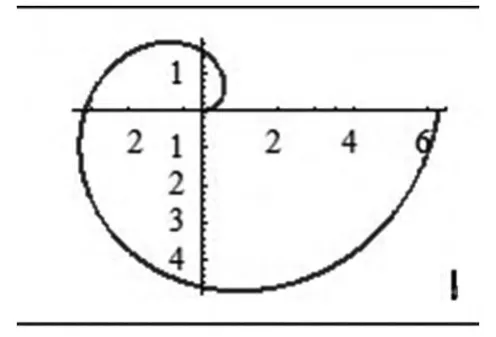
圖6

實例4 求阿基米德螺線ρ=θ相應于0≤θ≤2π段的弧長。下面的函數畫出了阿基米德螺線的圖像(圖6)。

2.2 在多元微積分教學中的應用

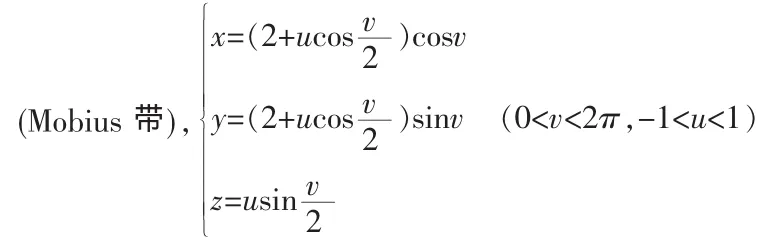
圖7

與一元微積分類似，多元函數的極限是學習多元微積分首先遇到的問題。一元函數y＝f（x）在x→x0時的極限是否存在，只需考慮在x0的左右極限即可。但是對于二元函數 z=f（x，y）在（x，y）→（x0，y0）時的極限是否存在，要考慮（x，y）沿任意方向趨向于（x0，y0），包括沿曲線，這一點使學生感到很困惑，老師的解釋通常也難有好的效果。利用Mathematica畫出相應函數的圖像和等高線，使學生能夠直觀地觀察到函數的幾何表述，可以很有效的解決這個問題。

3 結束語

Mathematica的繪圖功能是十分強大的，通過不同的設置和參數，結合教學內容，可以繪制出更為理想的圖形。在實際教學過程中，我們充分利用了繪制出的這些圖形，使抽象的內容變的直觀，進一步豐富課堂教學的內容，激發學生的學習興趣，調動了學生學習的積極性，改善了教學效果，提高了教學質量。

［1］王高峽.用Mathematica軟件繪制空間圖形的方法和技巧[J].重慶工學院學報:自然科學版,2007,7,21(7).

［2］高等數學[M].6 版.同濟大學出版社,2007,6.