從教育測量角度談2014年高考理科數(shù)學(xué)陜西卷的兩個問題

魏金寶 劉昕

摘 要： 從教育測量的角度分析2014年高考陜西理科數(shù)學(xué)卷，2014年高考理科數(shù)學(xué)的陜西卷的試卷編制，存在兩個不合理，一是測量點的賦分比例與其在課程中所占的課時比例顯著性不強，二是同一測量點上重復(fù)命題.

關(guān)鍵詞： 2014年高考理科數(shù)學(xué)陜西卷 教育測量 測試點 授課時數(shù)

一、試題的測量點及其賦分

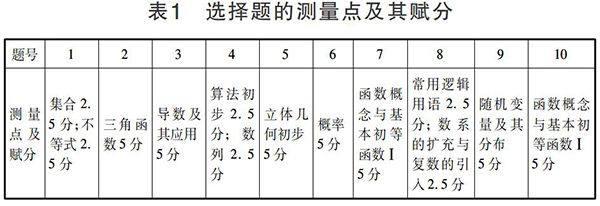
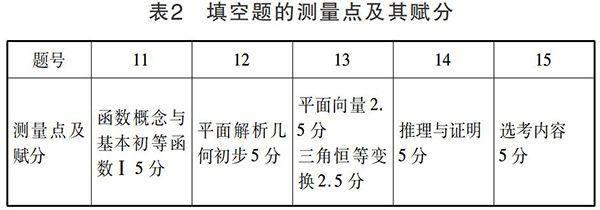
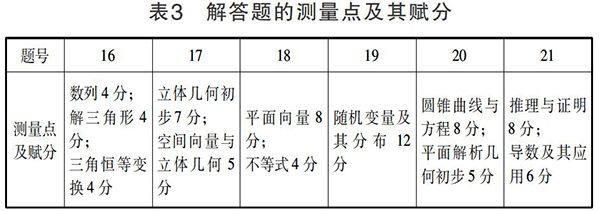
我們對2014年高考理科數(shù)學(xué)陜西卷每道題對應(yīng)的測量點，以及在該測量點上的賦分情況進(jìn)行了統(tǒng)計.測量點是將題目與《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（實驗）》（以下簡稱《課程標(biāo)準(zhǔn)》）中的“內(nèi)容與要求”對應(yīng)后確定的；測量點的賦分是根據(jù)題目的分值與題目所涉及的知識點確定的.以第1題為例：已知集合M={x|x≥0}，N={x|x■<1，x∈R}，則M∩N=（ ）（選項略去）.這道題的測量點是“集合”與“一元二次不等式及其解法”，分別對應(yīng)“數(shù)學(xué)1”中的“集合”和“數(shù)學(xué)5”中的“不等式”；本題的分值為5分，確定該題測量點及其賦分為“集合2.5分，不等式2.5分”.其中解答題的賦分還重點參考了試題的解答過程與評分參考，如果解答題有多種解法，則按評分參考所提供的解法1確定，具體統(tǒng)計結(jié)果見表1、表2和表3.

二、試卷存在的兩個問題

試題的難度指標(biāo)和區(qū)分度指標(biāo)，以及試卷的效度和信度是衡量一份試卷質(zhì)量的重要指標(biāo)，編制一份好的高考試卷，除了要以課程標(biāo)準(zhǔn)和考試大綱作為基本依據(jù)外，以上四個校標(biāo)將是最重要的指標(biāo).但以上四個指標(biāo)只有在試卷閱卷結(jié)束以后，根據(jù)學(xué)生的得分統(tǒng)計后才能得出.本文分析不涉及試卷本身的內(nèi)部一致性指標(biāo)及信度與效度析，以下僅從教育測量學(xué)的角度談?wù)勗嚲泶嬖诘膬蓚€問題.

1.測量點的賦分比例與其在數(shù)學(xué)課程中所占的課時比例之間的顯著性不強

依據(jù)課程標(biāo)準(zhǔn)要求，高中理科生需完成必修系列的5冊教材、選修2系列的3冊教材和選修4系列的2冊教材并取得相應(yīng)的學(xué)分，方可畢業(yè).依據(jù)人教A版教材教師教學(xué)參考用書中所給出的建議授課時數(shù)，這些課程總授課時數(shù)為324課時，各知識點的授課時數(shù)比例（百分?jǐn)?shù)）和各知識點在試卷中的賦分比例（百分?jǐn)?shù)），如表4.

高考是一種選拔性考試，它的主要測試目的是甄別和選拔學(xué)生，兼顧高中教學(xué)的導(dǎo)向作用.從教學(xué)角度看，試卷編制時應(yīng)考慮各知識點在試卷中所占的分值比例與其在總授課時數(shù)中所占比例之間保持一個大致的正比例關(guān)系.也就是說，花了更多時間學(xué)習(xí)的內(nèi)容，應(yīng)該是比較重要的學(xué)科內(nèi)容，在高考試卷中應(yīng)該賦以較大的分值，這樣才是科學(xué)合理的.我們采用統(tǒng)計數(shù)據(jù)處理軟件IBM SPSS Statistics 19分析“測量點占總課時百分?jǐn)?shù)”與“測量點占卷面總分百分?jǐn)?shù)”兩個變量的相關(guān)性，結(jié)果見表5.

*.在0.05水平（雙側(cè)）上顯著相關(guān).

從表5中可以看出，在該試卷中，測量點占課程總課時的百分?jǐn)?shù)與占卷面總分百分?jǐn)?shù)之間的相關(guān)性不強，它們之間的折線圖見圖1，散點圖見圖2.

如果測量點占課程總課時的百分?jǐn)?shù)與占卷面總分百分?jǐn)?shù)之間具有較強的相關(guān)性，散點圖上各點就應(yīng)該在一條直線附近波動.從圖1和圖2可以看出，測量點（知識點）的授課時數(shù)在數(shù)學(xué)課程中所占總授課時數(shù)的比例與測量點的賦分在試卷總分中所占的比例之間的相關(guān)性并不強，例如“統(tǒng)計與概率”與“推理與證明”兩個測量點上，其所占的課時比例并不高，但在試卷中所占的賦分比例卻高得驚人.相反，“統(tǒng)計”和“計數(shù)原理”兩個測量點上卻沒有命制試題.

2.同一測量點上重復(fù)命題

命制一套試題時，應(yīng)盡可能考查更多的知識點（雖然現(xiàn)在不片面追求知識點的覆蓋率），其中首先應(yīng)做到考查的知識點不重復(fù).另外，在試題命制過程中，一個首要的、重要的環(huán)節(jié)就是制定命題的雙向細(xì)目表，它對整個試卷題目命制起著宏觀的指導(dǎo)和調(diào)控的作用，更重要的是，按照雙向細(xì)目表命題可以有效避免在同一測量點上重復(fù)命題的錯誤做法.

2014年高考理科數(shù)學(xué)陜西卷第14題如下：

觀察分析下表中的數(shù)據(jù)：

猜想一般凸多面體中，F(xiàn)，V，E所滿足的等式是？搖 ？搖.

本題考查的內(nèi)容是歐拉公式，題設(shè)條件中給出了幾種多面體的面數(shù)（F）、頂點數(shù)（V）和棱數(shù)（E），如果學(xué)生記住了歐拉公式E=F+V-2，就可以直接寫出來了；如果學(xué)生沒有記住歐拉公式，甚至完全不知道歐拉公式，學(xué)生就可以由表格中的數(shù)據(jù)以歸納的方式猜想出來.可是，在課程標(biāo)準(zhǔn)與考試大綱中并沒有對歐拉公式的教學(xué)要求和考查要求，因此該題的測量點應(yīng)該是選修2-2第二章“推理與證明”的第一節(jié)“合情推理與演繹推理”.

2014年高考理科數(shù)學(xué)陜西卷第21題如下：

數(shù)學(xué)歸納法這一測量點在同一道試題中考查了兩次，顯然不是一個“合理不合理”的問題.數(shù)學(xué)歸納法在教學(xué)參考中的建議授課時數(shù)為2課時，屬于選修2-1第二章第三節(jié)的內(nèi)容，第二章《推理與證明》建議授課課時為8課時，8個課時的授課內(nèi)容，在一套試題中編制了4個（次）問題，這是極其不妥的.

以上從教育測量學(xué)角度對2014年高考理科數(shù)學(xué)陜西卷的兩個問題的分析，折射出高考數(shù)學(xué)試題命制技術(shù)、程序、過程的問題，也許還存在其他方面的隱性問題.我們希望這些問題不要重現(xiàn)，我們期待更規(guī)范的命制程序、更科學(xué)的命題方法、更高質(zhì)量的試題.