初中數學單元復習課的知識梳理淺析

吳冬梅

摘 要：數學單元復習課是數學課型之一，復習課的特點一是“理”，二是“通”， 復習課要引導學生把各知識點分類整理，形成完整的網絡，構建完整的知識體系，達到溫故知新，提高能力的目的。

關鍵詞：數學； 單元復習； 知識梳理

中圖分類圖：G633.6 文獻標識碼：A 文章編號：1006-3315（2014）12-015-002

一、數學單元復習課現狀

“復習課難上”這是許多數學老師經常發出的感嘆，老師感到難講，學生感到乏味。在復習過程中，我們往往會陷入簡單重復復習知識點或做題、講題、再做題的題海怪圈。中學數學《課程范式與實施策略》指出，復習課的教學目標要包括三個方面：1.梳理本章的知識結構，2.歸納總結解題方法，3.培養學生興趣，讓學生積極參與。可見，梳理本章的知識結構，主動歸納、建構一章的知識，是數學單元復習課的一個重要的環節。

二、數學單元復習課知識梳理的認識

數學是一門系統性很強的學科，現在新課程的知識點教學都是分模塊出現。復習課的特點之一是“理”，對所學的知識進行系統整理，使之“豎成線”、“橫成片”，達到提綱挈領的目的。特點之二是“通”，融合貫通，理清知識的來龍去脈，前因后果。因此，復習課必須針對知識的重點、學習的難點、學生的弱點，引導學生按一定的標準，把有關知識進行整理、分類、綜合，這樣才能搞清楚來龍去脈，彌補學習上的缺陷，減少記憶負擔，防止遺忘，促進學生認知結構的形成和完善，使學生對知識加深理解、牢固掌握、靈活運用，達到溫故知新，提高能力的目的。根據教學進度，可以分為單元復習、期中復習和期末復習。

三、數學單元復習課知識梳理的前提

“理解數學”是知識梳理的前提。理解數學就是要“了解數學知識的背景，準確把握數學概念、定理、法則、公式等的邏輯意義，深刻領悟內容所反映的思想方法，把握知識之間的多元聯系。對于復習課，我們更要把握每塊知識產生的背景，在教材中的地位、前后的聯系、后續學習的必要性，其中蘊含的數學思想方法有哪些，這些數學思想方法在學習其他知識時是否可以利用、類比推廣等”。所以我們只有理解數學，才能準確地確定教學目標，幫助引導學生形成科學、完善的知識結構。

“理解學生”是知識梳理的基礎。學生是教學的主體，問題的設計一定要從學生的認知水平出發，以學定“問”，充分考慮學生已有的經驗、學習基礎和思維特點，只有立足于學生的“最近發展區”，由淺入深，由感性到理性設計問題，才能真正引導和幫助學生思考問題、分析問題和解決問題。

“理解教學”是知識梳理的關鍵。理解教學就是要理解“教學活動是師生積極參與、交往互動、共同發展的過程。有效的數學活動是學生學與教師教的統一，學生是數學學習的主體，教師是數學學習的組織者、引導者與合作者，數學教學活動應激發學生興趣，調動學生的學習積極性，引發學生的數學思考，鼓勵學生的創造性思維”。

四、數學單元復習課知識梳理的策略

對于一節復習課最基本的原則是不能上成習題課和新課，需要教師精心設計。讓學生知識系統化、結構化的訓練非常重要。如何幫助學生梳理知識結構、建立知識框圖？

1.設計題組性問題，完善知識建構

在進行知識回顧時，配置包含所要復習知識的題組，讓學生通過解題來回顧基礎知識，運用所學知識，再在講評中幫助學生總結、歸納出知識的框架。編制題目前，教師應認真研讀課標和教材，根據復習目標和內容來選擇或設計題組；然后在課堂上給時間讓學生獨立完成，再通過師生、生生之間的交流了解學生的解答情況，強調需注意的事項。這樣能有效防止學生“小和尚念經，有口無心”的那種死記硬背數學概念、定理、公式等現象，較好地檢查學生基礎知識的掌握情況，大大提高復習效率。

案例1蘇教版數學七年級上“代數式”單元復習

（1）用代數式表示：①x的倍與3的差____；

②n的2倍除以m所得的商_____；

③鋼筆每支a元，鉛筆每支b元，小明買了2支鋼筆和2支鉛筆花費___元。

（2）你能再說出代數式“2a+2b”表示的一個實際意義嗎？

（3）剛才我們得到了代數式①x-3；②；③2a+2-b；若再增加代數式④-1，⑤-m2n；⑥2mn2-m2n-8，你能找出其中的整式嗎（用序號表示你是如何找的？）

（4）在所找出的整式中，哪些是單項式哪些是多項式？你是如何區分的？

（5）請說出你所找出的單項式-m2n的系數與次數。

（6）請說出你所找出的多項式2mn2-m2n-8的系數與次數。

（7）在多項式2mn2-m2n-8中有同類項嗎？你是如何確定的？

（8）試計算m2n-（2mn2-m2n-8），并求m=1，n=-2時這個代數式的值。你能由此歸納出整式加減的一般步驟嗎？

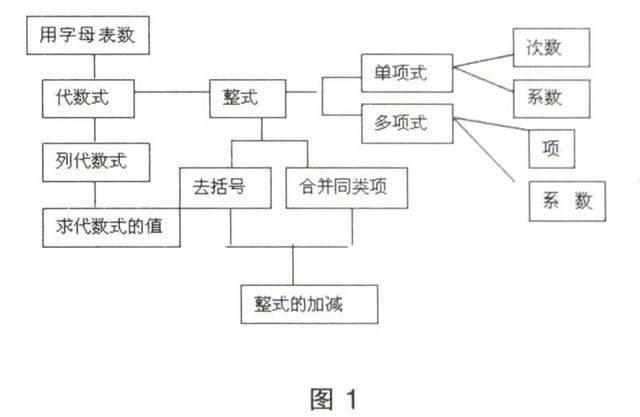
通過題組練習，讓學生說出解決問題時所用的知識點，能較好地檢查學生對代數式知識的掌握情況。在學生說出使用的知識點的同時，教師將重要的知識點進行板書，構建出全章的知識結構（如圖1），使復習內容條理清晰地呈現在學生面前，完成“由厚到薄”的學習過程。

2.設計多層面的開放性問題，完善知識建構

在復習課知識梳理階段，如果僅僅是羅列一些概念、結論，學生可能覺得乏味。如果教師能根據單元復習的內容和學生已有的知識儲備設計一些開放性、新穎性的探究問題，并將復習的主動權交給學生，（下轉第190頁）

（上接第15頁）讓學生根據自己對知識的認知，去主動、歸納、建構，這種單元復習課將呈現另一番精彩。

案例2蘇教版數學九年級上“圓”的單元復習

題目：如圖2，已知⊙M的圓心在x軸上，與坐標軸相交于點A、B、C、D，其中B點坐標（8，0），D點坐標為（0，-4）。

師：想一想，根據題目已有的信息，你能得到哪些結論，其中運用了哪些數學知識？

生1：由D點坐標（0，-4）及圓的對稱性，我得到C點坐標為（0，4）。

生2：我可以得到M點和A點的坐標。

師：你是怎樣求得？你的依據是什么？

生2：由△AOC∽△COB易求的A點的坐標為（-2，0），又OB+OA=10，所以半徑為5，從而得M（3，0）。

師：在圖2中，我們除了可以得到點的坐標外，還能得到什么？

生3：線段BC、AC的長度及其所在直線的解析式。

生4：∠ACB的度數。

生5：直角三角形、等腰三角形等基本圖形。

課堂伊始，教師首先用開放性問題引領學生回顧舊知識，因結論的開放性，給了學生更廣闊的思考空間；接著師生的交流讓學生主動構建知識，彌補了不同層次學生間知識的缺漏和思維的不足；最后的分塊梳理幫助學生從多角度看待問題，形成對知識深層次的理解，拓展了學生的知識面，之后教師只要進行簡單、適當補充，即可形成一個清晰的知識網絡。這一開放性探究，對學生的復習起到了“現行組織者”的作用，從而提高了單元復習課知識梳理的效能，激活了學生的思維。

3.設計活動化問題，完善知識建構

課標指出，“學生學習應當是一個生動活潑的、主動的和富有個性的過程。”動手實踐、自主探索、合作交流等都是學習數學的重要方式，也就是說，數學學習是一種活動，如同游泳一樣，要在游泳中學會游泳，我們必須在“做”數學中學習數學。

案例3 蘇教版數學八年級上“分式”單元復習

學具箱內有足夠多的卡片（紅色和藍色），每張卡片上標示一個簡單的整式或運算符號，如2，-1，3，x，1-x，+，-，____……

活動1 紅、藍兩方輪流拿出自己手中的兩張卡片，讓對方組成分式（8～10輪結束）。

按要求回答下列問題：

（1）對方組成的式子是分式嗎？

（2）如果是分式，它什么時候有意義？

（3）如果是分式，它的值能為零嗎？如果能，說出何時為零？

活動2 紅、藍雙方拿出自己手中的可以組成分式方程的卡片若干張，讓對方組成分式方程并正確解答（3～5輪結束）。

（1）對方組成的是分式方程嗎？

（2）對方解的分式方程正確嗎？

解決一個數學問題不是數學教學所追求的終極目標，引導學生在扎實掌握數學知識的基礎上，把各知識點分類整理，形成完整的網絡，構建完整的知識體系也很重要。唯有此，學生才能將所學數學知識點串成線，線連成面，才能對所學知識融會貫通，有個整體上的把握。

參考文獻：

[1]中學數學《課程范式與實施策略》

[2《中學數學教學參考》