齒根裂紋幾何參數對齒輪強度影響的研究
余清,朱江新,黃偉,吳海浪
(廣西大學機械工程學院,廣西南寧530004)
0 前言
齒輪作為工程機械變速箱的重要組成部件,是工程機械再制造過程中的一個主要組成部分。齒輪回收件根據檢測結果不同流向不同環節[1],為了研究齒根裂紋幾何參數對齒輪工作過程中應力集中情況的影響,將裂紋引入到齒輪副有限元分析模型中進行分析,對齒輪再制造具有重要意義。
1 齒輪幾何模型的建立
以柳工ZL855 裝載機變速箱輸出軸齒輪對為研究對象,齒輪材料為20CrMnTi,彈性模量EX為2.07 ×1011Pa,泊松比0.25,抗拉強度1 080 MPa,屈服強度835 MPa,其具體參數見表1。

表1 ZL855 裝載機變速箱輸出軸齒輪對參數
首先在UG 軟件中對齒輪副三維幾何模型進行參數化建模,然后導入到Ansys 中進行有限元分析,為了提高計算效率,在不影響計算結果的情況下,對模型進行簡化。簡化過程中,一般認為離齒根的深度達到1.5m、寬度達到6m時(m為齒輪的模數),齒輪體變形基本不再受影響,可以近似看作該處的實際位移為零[2],簡化后的齒輪副模型如圖1所示。
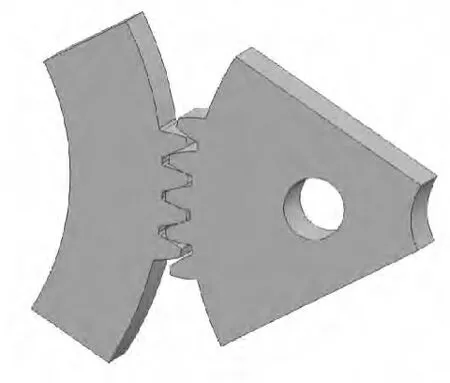
圖1 簡化的齒輪三維模型
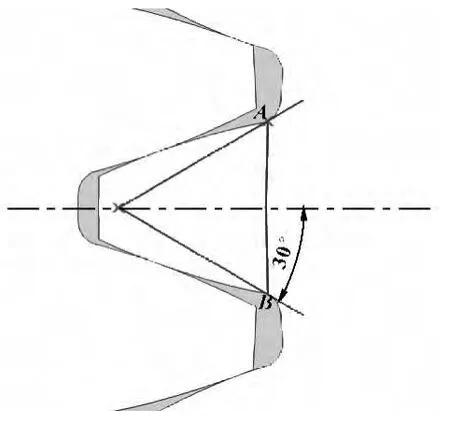
圖2 危險截面示意圖
2 齒根裂紋的引入
2.1 齒根危險截面的確定
要精確研究齒根裂紋對齒輪強度的影響情況,裂紋源出現位置的確定是關鍵。根據材料力學知識可知,構件最大內應力處強度最弱,是出現裂紋的危險截面。齒輪傳動過程中,齒根部分承受較大彎曲應力作用,因此齒輪危險截面處于齒根處,目前主流的齒根危險截面的確定是根據Hofer 提出的30°切線理論[3](與齒的對稱中線成30°角作齒根曲線的切線,切點的連線AB即為齒根的危險截面)來確定,如圖2所示。為了更準確地分析齒根裂紋對應力集中的影響,將裂紋沿齒根危險截面分布。
2.2 裂紋幾何參數的確定
齒根裂紋的主要參數包括寬度、深度、長度以及分布位置。在齒根危險截面上,裂紋可能隨機出現在任意位置上,為了研究不同分布位置的裂紋對齒輪強度的影響情況,文中在從動輪端部以及中部分別設置裂紋,其示意圖如圖3、圖4所示。
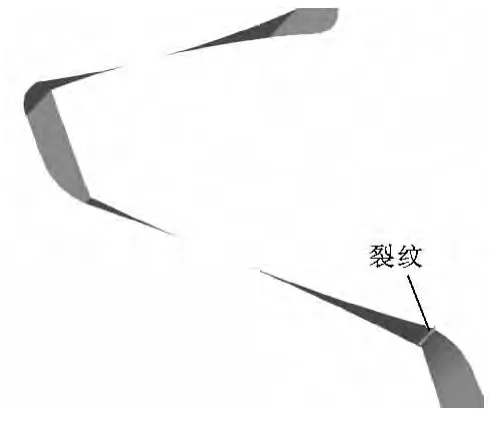
圖3 端部裂紋模型示意圖

圖4 中部裂紋模型示意圖
齒輪回收件中的裂紋主要是疲勞裂紋或沖擊裂紋,從裂紋產生到輪齒斷裂過程中,裂紋經歷著長度、寬度、深度3 個方向的擴展[4]。主要研究裂紋深度和長度對應力集中的影響,因此在齒根危險截面受拉一側的端面處及中部分別創建一系列寬度為0.1 mm 的微小裂紋,為了系統研究裂紋在深度和長度方向對應力集中的影響,根據裂紋擴展路徑[5-6],在深度上選擇0.1、0.2、0.3、0.4、0.5、0.6 mm 6 個值,長度上選擇0.5、1、2、5、10、20 mm 6 個值,共建立72 個帶齒根裂紋的有限元分析模型,并且假設齒輪模型除設定的裂紋外其他部分是連續且各向同性的。
3 齒輪三維靜態有限元分析
為了提高計算精度以及適應帶微小裂紋模型的網格劃分,選擇solid186 單元類型,采用自由網格劃分方式,網格精度為6,主動輪劃分為六面體網格,從動輪劃分為四面體網格,如圖5所示。
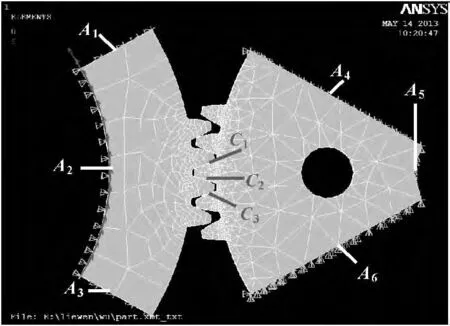
圖5 有限元分析模型
單齒嚙合區最高點是齒根彎曲應力最大的嚙合位置[7],為了分析齒跟應力分布,調整模型至剛好處于單齒嚙合的最高點,在設置接觸時,采用面接觸,設置C1、C2、C3三個接觸面,并且設置C2接觸對自動閉合。
施加載荷約束時根據齒輪傳動特性,在全局柱坐標系下,將A1、A2、A3三個面上的節點旋轉至全局柱坐標系下,并限制軸向和徑向自由度為0,而在A4、A5、A6三個面上施加全約束。為了施加貼近實際的載荷,將扭矩轉換成節點力施加在主動齒輪內圈節點上。其中主動輪內圈半徑為0.14 m,網格劃分后內圈上的節點數為475 個,計算公式如下:
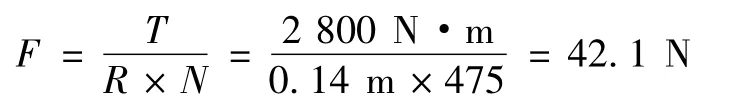
4 結果分析
通過有限元分析,可以得到無裂紋齒輪主、從動齒輪等效應力云圖,如圖6、7所示。
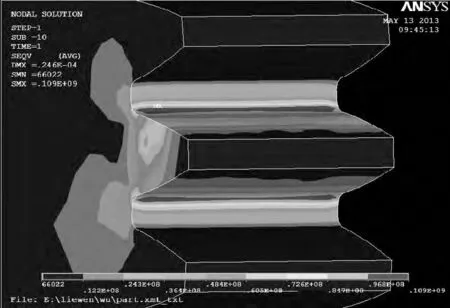
圖6 主動輪等效應力云圖
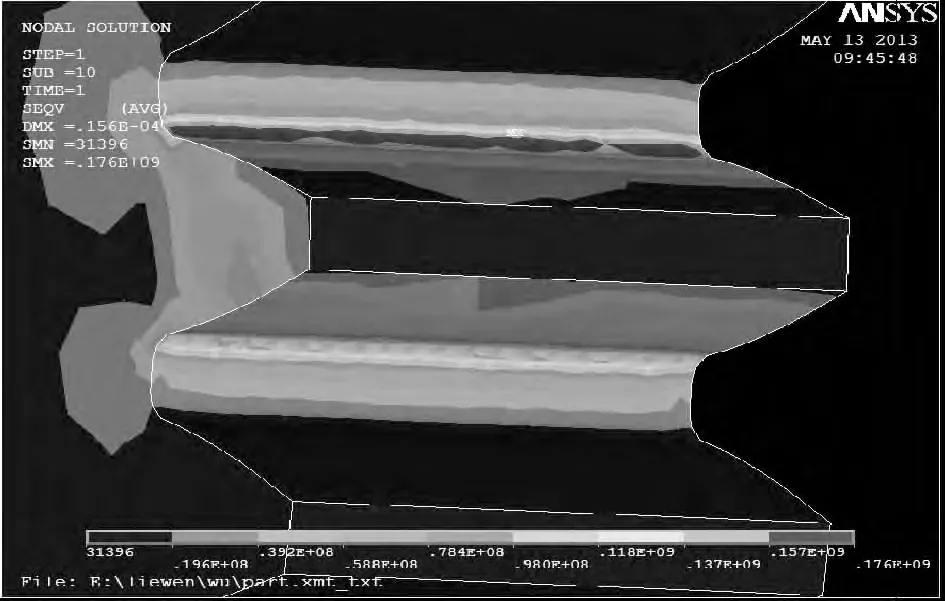
圖7 從動輪等效應力云圖
其中最大等效應力分別出現在主從動輪的齒根部分,主動輪最大等效應力108 MPa,從動輪最大等效應力為176 MPa,出現在齒根受壓一側,符合Hofer的30°切線理論,而從動輪齒根受拉側的應力為108 MPa,說明分析方法是合理正確的。
圖8—11 顯示了不同分布位置的裂紋處的最大等效應力在裂紋長度和深度方向的變化情況。
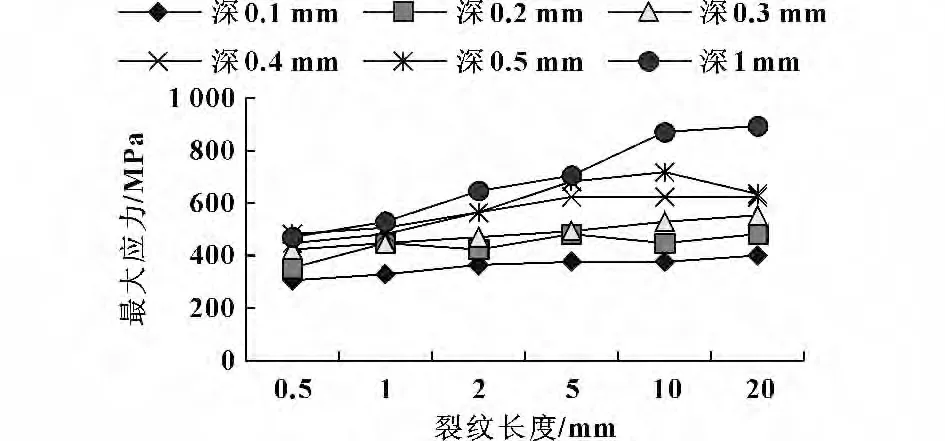
圖8 端部裂紋最大等效應力隨長度變化情況

圖9 中部裂紋最大等效應力隨長度變化情況
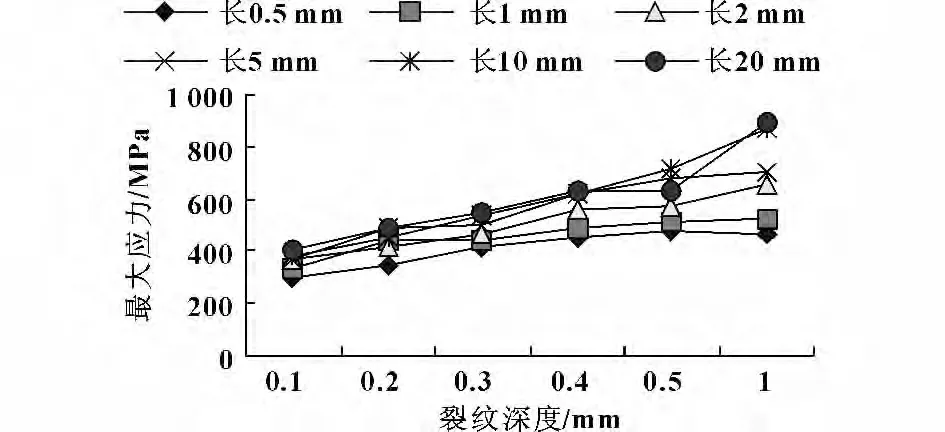
圖10 端部裂紋最大等效應力隨深度變化情況
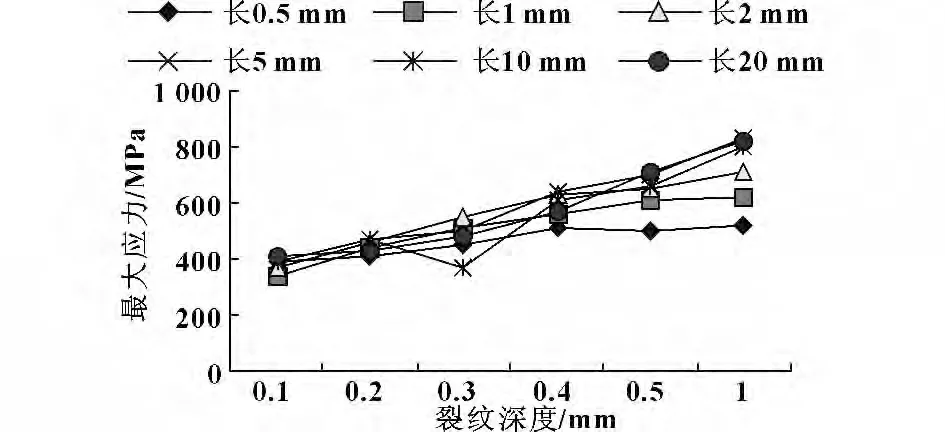
圖11 中部裂紋最大等效應力隨深度變化情況
從圖中數據可以得出以下結論:
(1)與無裂紋時齒根受拉側最大等效應力108 MPa 相比,裂紋處的最大等效應力變化范圍為301~890 MPa,因此齒根裂紋有明顯的應力集中作用;
(2)根據圖9 與圖8、圖11 與圖10 的對比,在相同幾何參數條件下,中部裂紋處的最大等效應力大于端部裂紋處的最大等效應力,因此中部裂紋對應力集中的影響較大;
(3)裂紋最大等效應力隨深度變化曲線斜率比裂紋最大等效應力隨長度變化曲線斜率大,因此裂紋深度對最大等效應力的影響比裂紋長度強。
5 結束語
使用有限元分析軟件Ansys 對帶裂紋的裝載機變速箱輸出軸齒輪對進行了靜態三維接觸分析。通過對設定了裂紋長度、深度及分布3 個不同參數的72 個帶裂紋齒輪模型進行三維有限元分析,得到了不同裂紋處最大等效應力結果,通過圖表形式對得到的分析結果進行對比研究,得出裂紋參數與裂紋處最大等效應力的相互關系,對給出齒輪裂紋極限判據具及對齒輪回收件再制造價值進行評估有重大的理論指導作用。
[1]張偉,劉仲謙,張紓,等.綠色制造與再制造技術研究與發展[J].中國表面工程,2006,19(5):76-81.
[2]莊競,袁衛華.TY320 型終傳動齒輪有限元分析及結構改進[J].工程機械,2006,37(10):31-34.
[3]李茹貞,趙清慧.齒輪強度設計資料[M].北京:機械工業出版社,1984.
[4]DAVID G Lewicki,ROBERTO Ballarini.Gear Crack Propagation Investigations[J].Tribotest,1998,5(2):157-172.
[5]David G,Lewicki.Effect of Rim Thickness on Gear Crack Propagation Path[J].NASA Technical Memorandum 107229,1996.
[6]LALONDE S,GUILBAULT R.Prediction of Thin-rimmed Gear Crack Propagation From a Factorial Design Approach[J].Fatigue & Fracture of Engineering Materials & Structures,201134(7):470-486.
[7]濮良貴,紀名剛.機械設計[M].北京:高等教育出版社,2007.

