基于形態學的一種齒輪故障特征提取方法

朱一，呂勇，侯高雁，黃浩

(1.中國人民解放軍96618 部隊，北京100085;2.武漢科技大學機械自動化學院，湖北武漢430081)

0 前言

數學形態濾波器［1］是一種針對非線性非平穩信號的特征提取方法，近年來在信號處理方面得到了廣泛的應用。其中形態差值濾波器用于提取信號中的正、負沖擊，而這種正、負沖擊正是所需要的故障信號。但是形態濾波器濾除白噪聲的能力卻不足，當故障信號中混有大量的白噪聲時，效果卻不好。針對形態學濾除白噪聲能力不足的問題，在特征提取之前先采用奇異值分解［2］(SVD)。近年來奇異值分解在信號降噪和微弱信號的提取［3］等方面獲得了廣泛的應用。奇異值反映了信號中有用信號和噪聲的能量分布情況，通過奇異值分解的信號特征提取方法難點在于奇異值分解階數的選擇。當信噪比不高時，奇異值分解可以將噪聲和特征信號分離開;當背景噪聲強烈時，通過奇異值分解難以將特征信號從噪聲中分離出來，故有必要在奇異值分解后再進行一次降噪。局域均值分解(LMD)是Jonathan S.SMITH［4］提出的一種自適應非平穩信號處理方法，該方法不僅分解速度快，而且能夠很好地抑制端點效應。近年來該方法在信號的降噪方面取得了很好的結果［5］。

基于以上原因，提出將3 種方法相結合，首先將信號進行奇異值分解，對分解后的主要成分取均值，然后進行LMD 分解實現二次降噪，選取主要分量求和重構，最后通過形態學差值濾波器來提取信號特征。將該方法應用于齒輪故障信號分析中，成功提取出了齒輪故障特征頻率。

1 基于奇異值分解、局部均值分解和形態濾波的特征提取方法

1.1 形態濾波

數學形態學是基于隨機集理論與積分幾何建立起來的不同于時域、頻域分析的非線性方法。形態學是使用結構元素探針在信號中不斷移動來提取有用信息，進行特征分析和描述。起初主要用于圖像處理中，隨后在信號處理方面得到了廣泛的應用［6］。

膨脹和腐蝕是數學形態學的兩種基本算子。設f(n)為定義在F={0，1，2，…，N-1}的一維時間序列，g(n)為定義在G={0，1，2，…，M-1}的一維結構元素序列，其中N和M都是整數，且有N≥M。則f(n)關于g(n)的膨脹、腐蝕、開運算和閉運算分別定義為:

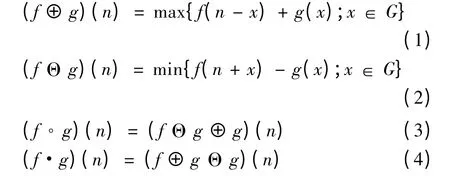
式中:⊕為膨脹運算;Θ 為腐蝕運算;。為開運算;·為閉運算。

膨脹運算可以抑制正沖擊，平滑負沖擊;腐蝕運算可以平滑正沖擊，抑制負沖擊;開運算用于抑制邊界上的毛刺;閉運算用于平滑邊界上的凹陷部分。

由形態學開、閉運算的組合，可以構建平均濾波器(AVG)和差值濾波器(DⅠF)。

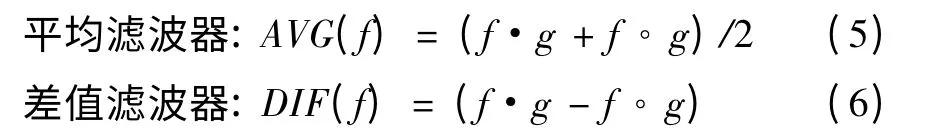
平均濾波器可以消除信號中的正、負沖擊，對信號起到平滑作用;而差值濾波器可以提取信號中的正、負沖擊。采用差值濾波器來提取微弱信號，結構元素選擇扁平的圓盤形結構元素，尺寸選擇通過遺傳算法來尋求最優解，按照公式(7)用信噪比來衡量，信噪比最小的為最優的結構元素大小。其中Y為信噪比，y1為原始信號的平方和，y2為噪聲信號的平方和。

數學形態學有很強的抑制脈沖干擾的能力，但濾除白噪聲的能力卻不足，在形態學差值濾波器提取故障信號之前，有必要進行降噪處理。

1.2 奇異值分解

對于任何一個矩陣設X，必定存在兩個正交矩陣Um×m=(u1，u2，…，ur，ur+1，…，um)和Vd×d=(v1，v2，…，vr，vr+1，…，vn)，使得X=UDVT。其中，(i=1，2，…，r，…，d)稱為矩陣X的奇異值。

奇異值反映了有用信號和噪聲的能量集中情況，較大的奇異值主要反映有用信息，較小的奇異值主要反映噪聲，選擇合適的分解階數即可將噪聲和有用信號分離開，提取出有用信號。文中嵌入維數選擇10，分解階數選擇5，多次嘗試發現分解階數為5 時效果比較好。為了克服選擇分解階數不當的問題，選擇局部均值分解進行二次降噪，突出微弱信息。

1.3 局部均值分解

LMD 的實質就是將非平穩調制信號分解成一系列PF分量，每一個PF分量由一個包絡信號和一個純調頻信號的乘積而得，對于原始信號x(t)，LMD分解具體步驟如文獻［4］:

經過LMD 分解后，初始信號x(t)被分解為k個PF分量和uk(其中uk為殘余項)之和，即:

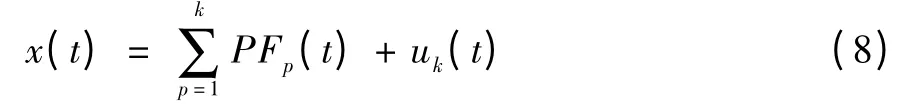
局部均值分解后，將能量高的PF分量進行求和重構，選擇前3 階PF分量。

所提出的方法具體的技術路線如圖1所示。

圖1 技術路線圖

2 數值仿真試驗

采用的仿真信號如下:

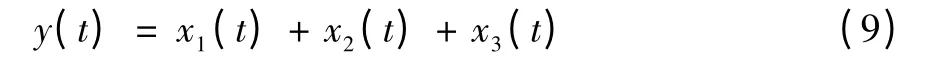
式中:x1(t)=2.2cos(60πt)+1.5cos(100πt)，是頻率為30 Hz 和50 Hz 的諧波信號;x2(t)為高斯白噪聲;x3(t)為頻率為20 Hz，周期內沖擊函數為exp(-20t)sin(20πt)的周期性指數衰減沖擊信號，其中采樣頻率為1 000 Hz，采樣時間為2 s。此實驗是為了抑制白噪聲和諧波信號，提取頻率為20 Hz 的沖擊成分，得到的仿真信號如圖2所示，圖3 為仿真信號的頻譜圖，只能看到頻率為30 Hz 和50 Hz 的諧波信號，沖擊成分完全被淹沒。

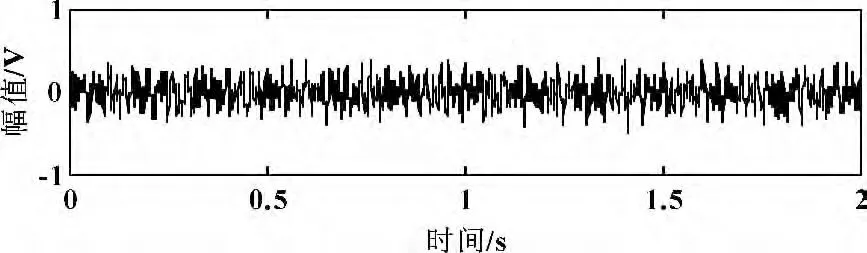
圖2 混合信號的時域圖

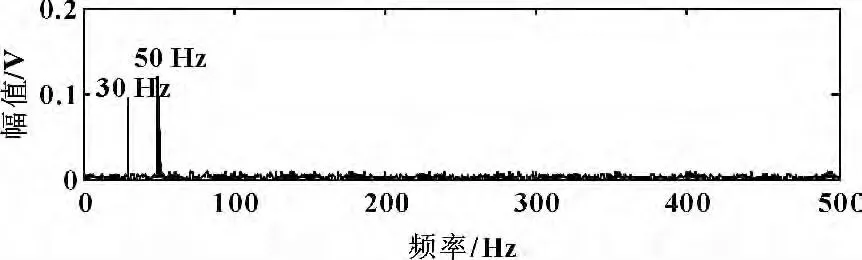
圖3 混合信號的頻域圖

采用提出的方法，得到的結果如圖4所示，清晰地提取出20 Hz 的沖擊成分以及其倍頻信息。

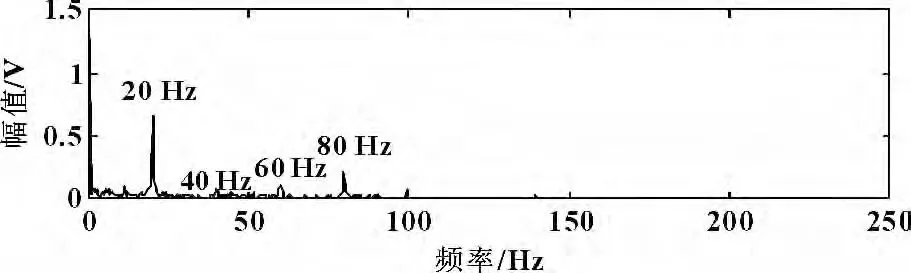
圖4 處理后的結果

3 齒輪局部故障實驗

通過齒輪斷齒和磨損兩種故障來驗證該方法，齒輪作輕微損傷，同時加大環境噪聲污染，將所提出的方法與奇異值形態濾波法相比較。在齒輪箱故障診斷試驗平臺上進行實驗，齒輪箱為1 級降速傳動，輸入軸轉速為363 r/min，大齒輪和小齒輪的齒數分別為37 和20，模數為3，傳動比為1.85，采樣頻率為2 000 Hz，采樣時間為1 s。如圖5(a)所示為齒輪斷齒信號的時域圖，圖5(b)為齒輪磨損時域圖。

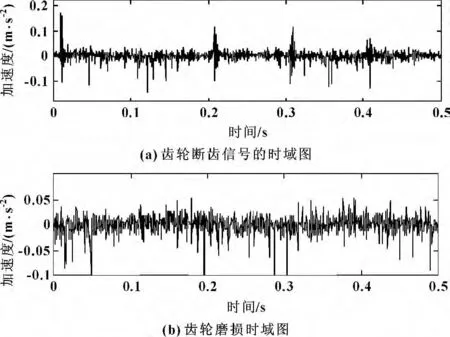
圖5 齒輪斷齒和磨損時域圖

圖6(a)和圖6(b)相比，兩種方法都可以提取到故障信號及其倍頻信息。奇異值濾波法采用一次降噪后用形態差值濾波提取故障信號，而文中的方法是在奇異值分解后，采用局部均值分解再進行一次降噪，然后用形態濾波提取故障信號，經過兩圖相比，所提出的方法提取出來的故障信號和其倍頻信號的幅值更高，更明顯。圖7(a)與圖7(b)相比，也同樣可以看出采用文中提取出故障特征的效果更好。

齒輪斷齒信號和齒輪磨損信號經過兩種方法處理后的結果分別如圖6 和圖7所示。

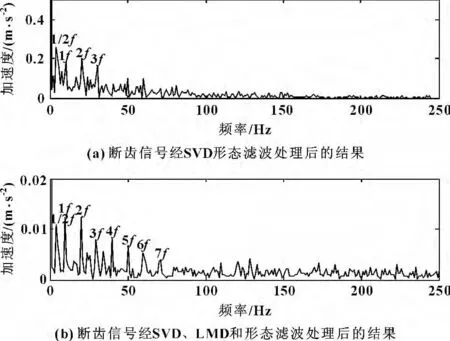
圖6 斷齒信號經過不同方法處理后的結果

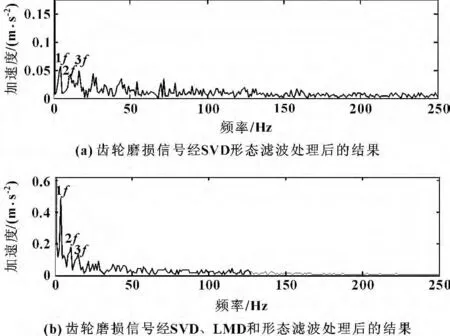
圖7 齒輪磨損信號經過不同方法處理后的結果

4 結論

通過仿真試驗和齒輪故障模擬實驗，證明了所提出方法的有效性。并與SVD 形態濾波法相比較，該方法提取出的故障信號的頻率特征效果更好，證明了該方法是一種有效的信號特征提取方法，主要結論如下:

(1)通過雙重降噪克服了形態差值濾波器濾除白噪聲能力不足的問題，成功地從齒輪故障信號中提取出信號頻率特征。

(2)將該方法與SVD 形態濾波法相比較，該方法能夠有效地提高信噪比，突出故障特征，提取出故障信號的效果更好，更適合于從強背景噪聲中提取出微弱信號。

［1］SERRA J.Morphological Filtering:an Overwiew［J］.Signal Process，1994，38(4):3-11.

［2］CEMPEL C.Generalized Singular Value Decomposition in Multidimensional Condition Monitoring of Machines—a Proposal of Comparative Diagnostics［J］.Mechanical Systems and Signal Processing，2009，23(3):701-711.

［3］喬鐵柱，路曉寧，王福強.鋼繩芯輸送帶的磁記憶信號特征提取方法研究［J］.煤礦機械，2011，32(9):261-263.

［4］SMITH S J.The Local Mean Decomposition and Its Application to EEG Perception Data［J］.Journal of the Royal Society Interface，2005，2(5):443-454.

［5］鞠萍華，秦樹人，趙玲，等.基于LMD 的能量算子解調方法及其在故障特征信號提取中的應用［J］.振動與沖擊，2011，30(2):1-5.

［6］魏濤，王召巴，金永.煤炭輸送帶表面裂紋自動檢測技術研究［J］.煤礦機械，2010，31(2):211-213.