基于VAR模型的麗水市金融深化與創新集聚關系的實證分析

周宏蕓

（麗水學院商學院，浙江麗水323000）

【區域經濟】

基于VAR模型的麗水市金融深化與創新集聚關系的實證分析

周宏蕓

（麗水學院商學院，浙江麗水323000）

基于VAR模型，利用1985—2012年的數據對浙江省麗水市創新集聚水平與金融深化之間的長期動態關系進行實證分析。結果表明，兩者之間具有長期動態均衡關系，而且金融深化對麗水市創新集聚有著長期顯著的拉動作用。但是創新集聚還不是金融深化的Granger原因，說明目前麗水市尚未建立金融深化與創新集聚之間的循環互動機制。

金融深化；創新集聚；VAR模型；脈沖響應

金融深化是麗水市金融改革的重要組成部分，也是金融政策體制的進一步完善。麗水市生態產業集聚區作為浙江省14大省級產業集聚區之一，承擔著生態保護重任的同時，必須突破經濟資源的各種束縛，將產業發展盡快轉移到依靠科技進步與創新的軌道上來。現代市場經濟條件下，創新生產多在區域集聚的模式下進行。這種創新集聚能夠促進信息溢出、傳播和共享，增強創新的競爭力，降低知識傳遞成本，進一步促進創新生產活動的發展。因此，創新集聚是麗水市生態產業集聚發展的立足點和驅動力。在麗水市積極建設生態產業集聚區的過程中，研究金融深化與創新集聚的關系對麗水市經濟實現跨越式發展有著重要的現實意義。

一、指標選取與數據預處理

（一）創新集聚水平（INV）

借鑒產業集聚指標構建原理，本文采用區域面積上承載的專利總量測算麗水市的創新集聚水平，即其中，Patt為本地區t時期的專利量，St表示本地區t時期的面積。考慮到數據的可獲得性和客觀性，本文采用1985-2012年各年專利授權量來衡量專利數量，利用各年每平方公里的專利授權數來反映本地區當年的創新集聚水平。

（二）金融深化水平（FIR）

由于中國的金融深化過程主要體現為金融增長，如金融機構與金融資產數量上的增長［1］，再加上統計數據的相關限制，本文參照前人做法［2］，選取規定期間內同一區域的金融資產與生產總值的比率來衡量麗水市金融深化程度。其中金融資產用該地區當年存貸款余額表示。

（三）數據的預處理

為了消除數據中可能存在的異方差，我們對上述指標變量分別取自然對數后得到LINV和LFIR。

二、模型的建立與分析

Sims（1980）等人提出的向量自回歸模型（VAR），是將同一樣本期間內的每一個內生變量作為他們滯后值的線性函數，通過聯立方程的模式對全部變量間的動態關系進行估計。其數學形式表述為：yt＝c＋A1yt－1＋·· ·＋Apyt－p＋εt，其中，c為n×1常數向量，A1，···，APi是n×n系數矩陣，εt是n×1擾動向量。本文將利用VAR模型對麗水市金融深化與創新集聚的關系進行實證檢驗。

（一）模型構建前的準備

本文根據ADF值對上述變量的平穩性進行單位根檢驗。根據單位根的檢驗結果可知，LINV和LFIR這兩個時間序列是一階單整序列。為此，本文采用EG兩步法對其間的關系進行協整檢驗。結果發現，變量LINV和LFIR的殘差序列在95%顯著水平下是平穩的，即LINV和LFIR存在長期協整關系。可見，利用LINV和LFIR直接建立VAR模型是可行的。

（二）模型的建立

根據模型滯后結構確定準則的篩選結果，確定VAR模型的滯后期為1，即建立VAR（1）。VAR（1）模型方程如下：

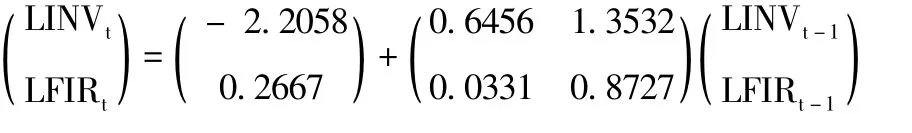
VAR（1）的兩個特征根系數分別為0.518924和0.999389，均小于1，皆位于單位圓內（如圖1），因此該模型的結構是穩定的。

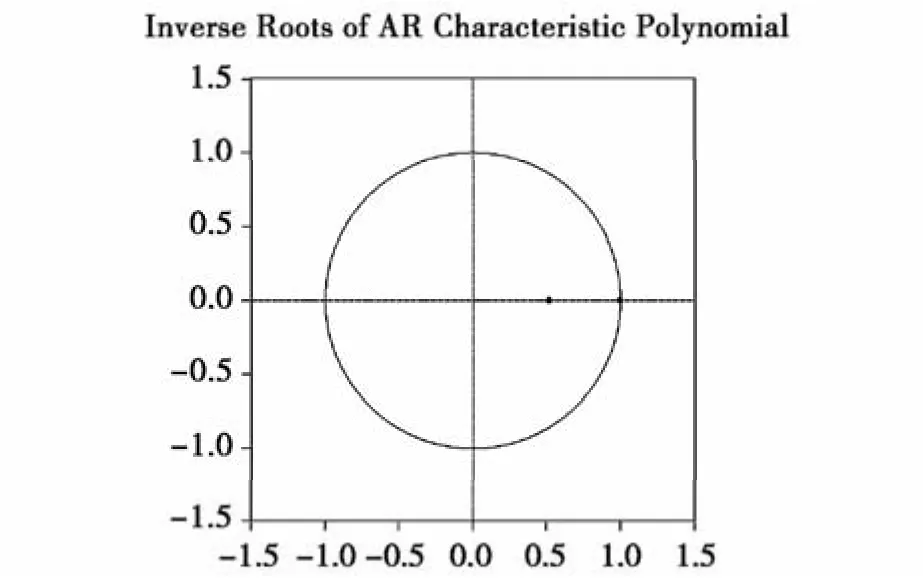
圖1 VAR（1）的AR特征多項式逆根

（三）模型分析

為了便于下面的脈沖響應分析，本文對VAR（1）中的變量進行Granger因果檢驗。

從表1的結果可以看出，在5%的顯著水平下，金融相關率（LFIR）是創新集聚水平（LINV）的Grange原因，表明金融深化水平確實影響了麗水市的創新集聚水平。而創新集聚水平不是金融相關率的Grange原因，這說明麗水市金融深化水平還處于比較低的階段，創新集聚水平的提升并沒有反過來促進金融深化，金融深化與創新集聚相互促進的循環機制還尚未建立。這與麗水市經濟金融發展落后、金融市場尚不成熟的特征相符。

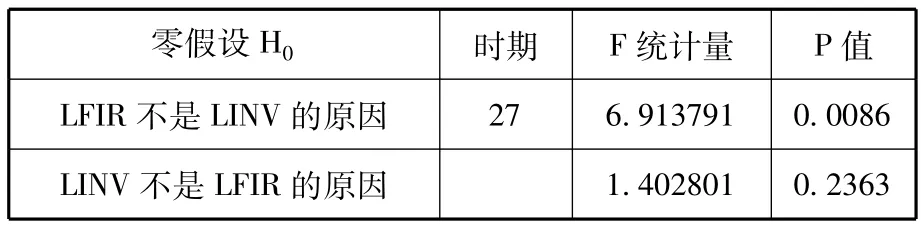
表1 Grange因果檢驗結果

根據實際分析的需要，并結合Grange檢驗結果，下面分別給創新集聚水平（LINV）和金融相關率（LFIR）一個正的單位大小的沖擊，得到關于創新集聚水平（LINV）的脈沖響應函數圖。從圖2a可知，創新集聚水平（LINV）對遭受自身的沖擊是正向響應，且在沖擊當期達到最高值，之后開始收斂。圖2b說明，當給金融深化水平（LFIR）一個正向沖擊后，會帶來創新集聚水平（LINV）正向的響應，但是這種響應表現為長期持續的反應，并沒有在沖擊當期體現出來。這表明金融深化對創新集聚的促進作用具有滯后性，這種正面的影響將長期持續存在。

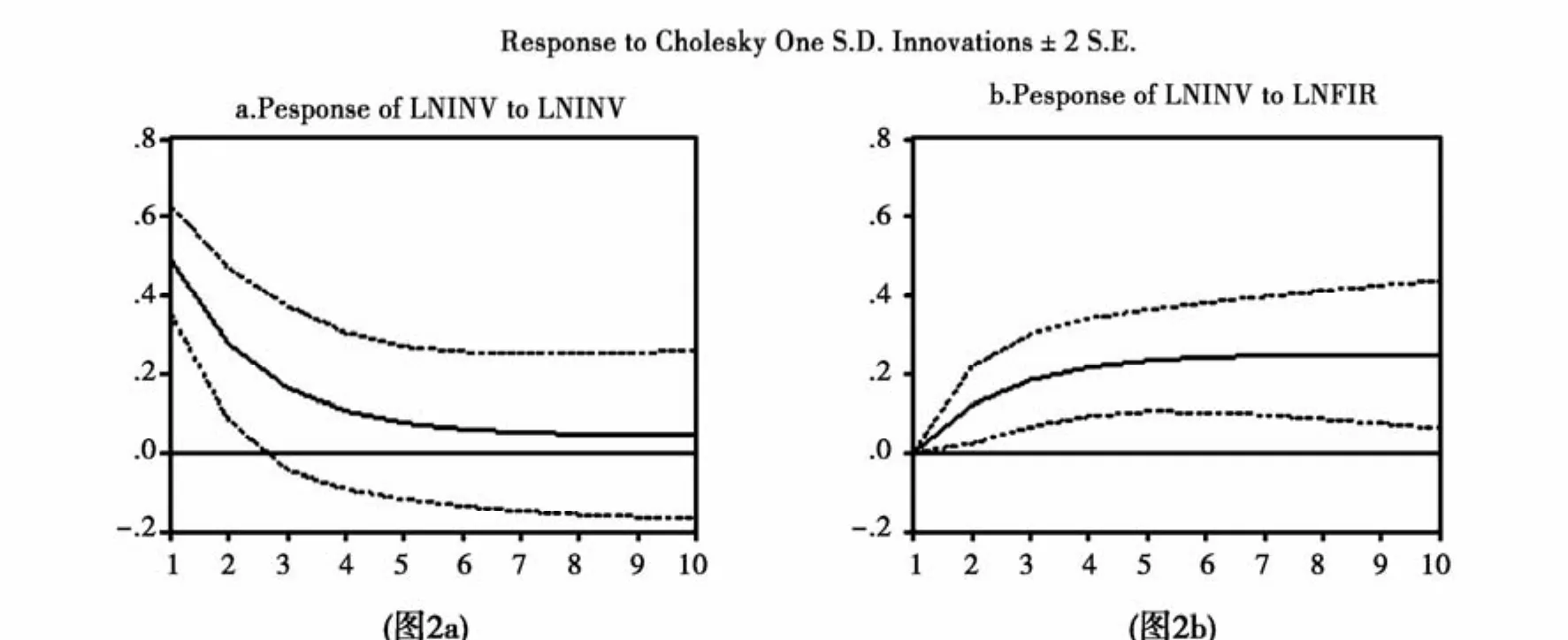
圖2 創新集聚水平對各影響因素的脈沖響應函數曲線

脈沖響應函數是為了追蹤各變量對系統中某一個或若干個變量沖擊的效果，而方差分解法會將系統中某變量的預測均方誤差分解為由系統中各變量沖擊所帶來的影響部分，記錄系統中每個變量沖擊對該變量的預測均方誤差的貢獻，從而了解各信息對模型內生變量的相對重要性［4］。如圖3a，自身因素的變化對創新集聚水平（LINV）變化貢獻率呈現出逐年遞減的趨勢，在第10期該貢獻率降至50%以下。圖3b顯示，金融深化水平（LFIR）變動對創新集聚水平的貢獻率雖然在前2期比較低，但呈逐年遞增的趨勢，于第9期其貢獻率超過了50%，高于同期創新集聚水平的貢獻率。這一結果與脈沖響應函數相吻合，說明金融深化對創新集聚水平的促進作用需要通過較長一段時間顯現，并且這種作用會越來越強。

三、結論

基于以上模型分析，得出以下結論：麗水市金融深化與創新集聚具有長期動態均衡關系，其中金融深化對麗水市創新集聚有著長期顯著的拉動作用；但是麗水市的創新集聚還不是金融深化的Granger原因，說明目前麗水市金融深化與創新集聚之間的互動循環機制尚未建立。可見，促進金融深化、建立金融深化與產業創新集聚之間的長效互動機制是麗水市實現經濟跨越發展的必然選擇。為此，麗水市應以創建生態產業集聚區為契機，深化金融改革，完善生態產業集聚創新的金融支持制度；通過加快金融機構多元化發展步伐，豐富和創新金融產品，進一步擴大金融規模；通過完善金融市場，促進市場機制對創新性資源的合理、有效配置。

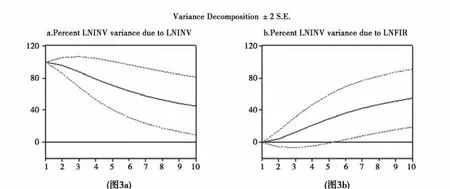
圖3 創新集聚的方差分解結果

［1］賈春新.金融深化：理論與中國的經驗［J］.中國社會科學，2000（3）.

［2］任力，黃崇杰.中國金融發展會影響能源消費嗎？——基于動態面板數據的分析［J］.經濟管理，2011（5）.

［3］李瑋，張榮霞，梁文群，趙國浩.基于VAR模型的技術進步對能源強度的脈沖響應分析——以山西省為例［J］.工業技術經濟，2012（4）.

［4］Hicks J.A Theory of Economic History［M］.Oxford：Clarendon press，1969.

［5］King R G，Levine R.Finance and Growth：Schumpeter Might Be Right［J］.Quarterly Journal of Economics，1993.108.

（責任編輯：梁宏偉）

F832.7

A

2095－3283（2014）09－0093－03

周宏蕓（1982－），女，漢族，碩士研究生，講師，研究方向：區域經濟。

2013年麗水市社科聯課題（項目編號：LC201319）。