并列建筑物周圍風場的數值模擬
陳善群,田順年,廖 斌,楊 明
(1.安徽工程大學 建筑工程學院,安徽 蕪湖 241000;2.中國中鐵四局重慶分公司,重慶 400010)
近些年來高層建筑得到了飛速發展,風荷載是高層建筑的主要控制荷載,風對高層建筑以及建筑物周圍環境的影響巨大.在人們日益關心人居環境的今天,有必要對高層建筑物周圍風場和風壓進行全方面系統地研究,為評估建筑的城市規劃及建筑設計的合理性提供重要的參考數據.
國內外學者對建筑周圍風環境進行了大量數值模擬.R.Yoshie等人[1]使用k-ε模型、DSM、RANS以及LES等湍流數值模型對日本東京現實街區(新瀉、新宿)建筑群風場模型進行數值模擬.B.Blocken和J.Carmeliet[2]使用CFD方法在不同風向、不同風速條件下,對不同類型的高層住宅建筑繞流風場進行數值模擬,找到了在高層住宅建筑戶外使人感覺到舒服的風場條件.湯廣發等[3]對一棟10m×10m×10m的建筑物采用k-ε湍流模型進行繞流計算,得到了建筑物表面壓力分布及建筑周圍速度矢量圖.馬劍等[4]采用基于Reynolds時均N-S方程和RNGk-ε湍流模型的數值研究方法,分別對具有風洞試驗結果的單幢方形截面建筑和多幢矩形截面建筑組成的建筑群周圍的風環境進行了數值模擬.雖然對建筑風環境的研究顯示了蓬勃生機,但大多集中在對單個建筑物的研究,對多個建筑物建筑物繞流及其相互干擾問題的研究較少.建筑物群周圍風繞流特性更加復雜,對數值模擬提出了更高的要求.
本文擬采用標準k-ε湍流模型對并列建筑群風場進行數值模擬,研究單體建筑物高度、并列建筑物高差及并列建筑物間距等因素對并列建筑周圍風場變化的影響.
1 建筑物風場的數值模擬理論
1.1 控制方程
建筑物風場湍流流動的基本控制方程為Navier-Stokes方程組[5],包括連續性方程和動量方程.在笛卡爾坐標系下,將連續性方程和動量方程以張量形式寫出,分別為:

對連續性方程和動量方程分別進行時均化處理,得到基于雷諾平均的連續性方程和動量方程:

式中,xi為空間位置坐標為i方向的時均速度;ˉP為時均壓力;ρ為空氣密度;μ為空氣動力粘性系數,為雷諾應力.
1.2 標準k-ε模型
標準k-ε模型是建立在半經驗公式模型的基礎上,模型輸運方程組源于湍流動能k和湍流耗散率ε.本文采用應用最廣泛也最成熟的標準k-ε兩方程模型.其中,湍流動能k方程:

湍流耗散率ε方程:

由于本文所模擬的計算模型為定常工況條件下,可將動量方程(4)、湍流動能k方程(5)和湍流耗散率ε方程(6)簡化為如下形式:
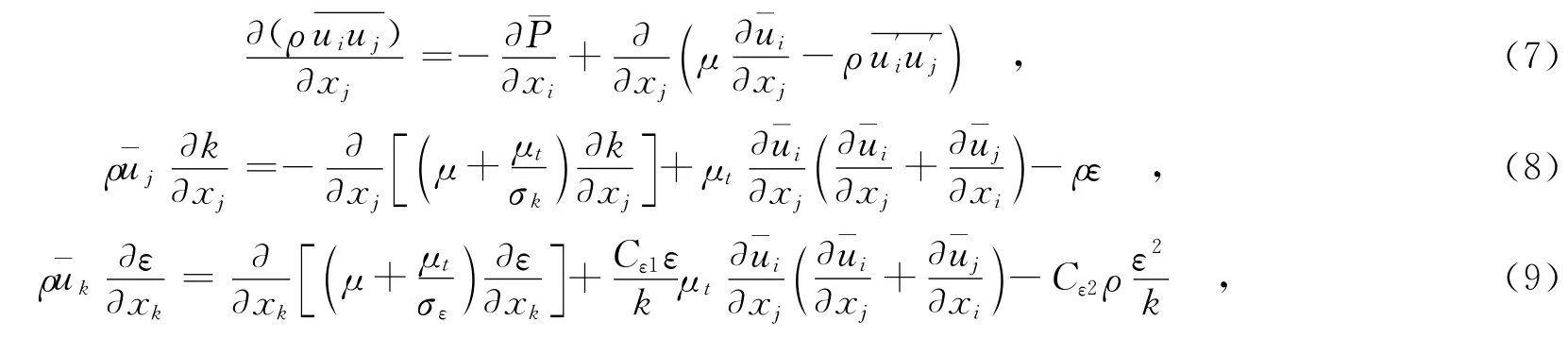
式中:μt為湍流動力粘度,表達式為為模型常數,取值為Cμ=0.09,Cε1=1.44,Cε2=1.92,σk=1.0,σε=1.3.
2 方柱繞流模擬驗證
2.1 計算模型的建立

圖1 方柱繞流計算域
方柱繞流計算域如圖1所示,放置在通道中軸線上的立方體柱邊長H為50mm,計算區域長1 250mm,寬為300mm,高為100mm.計算區域采用非均勻網格,靠近方柱區域網格布置較密集,計算域邊界網格較稀疏的,最小網格間距小于2.5mm.通道高作為特征長度計算的雷諾數與Martinuzzi和Tropea的實驗取值一致.
2.2 邊界條件的設定
入口邊界條件:速度入口條件,設定空氣流的水平速度恒為1.6m/s,其他方向的速度梯度為零,壓力在各個方向的梯度為零.出口邊界條件:壓力出口條件,即沿著出口方向的壓力梯度為零.表面(壁面)邊界條件:采用固壁無滑移邊界條件,即速度在各個方向的梯度為零,壓力的法向倒數也為零.
2.3 計算結果與分析

圖2 X=31.25mm,Y=0處流向速度對比

圖3 X=50mm,Y=0處流向速度對比
Y=0處,X=31.25mm、X=50mm截面x方向速度與實驗數據的對比結果如圖2、圖3所示.其中U/Ue表示計算速度與來流速度的比值;Z/H表示z方向坐標值與模型高度H的比值.由圖3可知,本文數值計算結果與實驗數據吻合良好,驗證了建筑物風場的數值模擬理論在建筑物風場數值計算中具有相當的精確度和良好的適用性.
3 并列建筑物周圍風場數值模擬與分析
3.1 并列建筑物計算模型的建立
對于并列建筑物共設置兩單體建筑模型,如圖4所示,其建筑底部截面為邊長L為20m×20m的正方形.計算域長寬均為200m,高度取較高建筑高度的兩倍,速度入口界面距并列建筑60m.兩建筑高度分別為H1、H2,建筑物之間間距為D.

圖4 并列建筑物風場計算域
為研究單體建筑高度、并列建筑高差及并列建筑間距等因素對并列建筑周圍風場變化的影響.本文共建立了10種不同參數的并列建筑物風場模型,各種模型參數如表1所示.計算域網格的劃分如圖5所示.在三維模型壁面處附近用非結構性網格進行加密,較遠處采用均勻網格,其網格間距最小尺寸取值在1~4m之間.并列建筑物模型其網格單元數在40萬左右.

圖5 并列建筑物風場計算域網格總體劃分

表1 各種模型參數分項表
3.2 邊界條件的設定
入口邊界條件:速度入口條件,按照對應實際中6級強風(風速10.8~13.8m/s),本次風場模型中取11.0m/s,即設定空氣流的水平速度恒為11.0m/s,其他方向的速度梯度為零.出口邊界條件:壓力出口條件,即沿著出口方向的壓力梯度為零.表面(壁面)邊界條件:采用固壁無滑移邊界條件,即速度在各個方向的梯度為零,壓力的法向倒數也為零.
3.3 計算結果與分析
(1)并列建筑物高度H1=H2,兩建筑物之間間距D相等.模型1、3、10間隔中心截面速度沿高程變化如圖6所示.由圖6中可知,3種模型速度變化曲線都可分為上升段和平緩段.上升段是近地面處,由于地面的阻滯作用,風速較小,隨著高程上升,風速快速上升直到極值點,在后方平穩段,風速有緩慢下降并逐漸趨于穩定.在兩建筑物之間間距D相等的條件下,隨著建筑物高度的增加,間隔中心截面速度呈上升趨勢且速度極值點高程同樣呈上升趨勢,但風速平穩段速度大小呈下降趨勢.
(2)并列建筑物高度H1=H2,兩建筑物之間間距D不相等.模型3、6、7間隔中心截面速度沿高程變化如圖7所示.由圖7可知,在兩建筑物高度H1=H2且保持不變的條件下,隨著兩建筑物之間間距D的逐漸減小,速度變化曲線凹凸變化愈發明顯,甚至可以清楚地發現,當并列建筑物間隔過小,不超過建筑高度的1/8時,風速大小甚至減小到0,即風無法正常通過兩建筑物的間隔.
(3)并列建筑物高度H1≠H2,兩建筑物之間間距D相等.模型2、3和模型8、9間隔中心截面速度沿高程變化如圖8所示.由圖8可知,在兩建筑物之間間距D相等的條件下,并列建筑物高度H1≠H2時,模型2、3和模型8、9間隔中心截面速度變化趨勢非常接近,說明并列建筑兩建筑物高度差對間隔中心截面速度影響比較小.
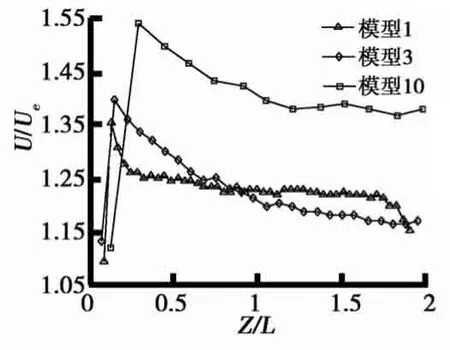
圖6 模型1、3、10間隔中心截面速度沿高程變化

圖7 模型3、6、7間隔中心截面速度沿高程變化

圖8 模型2、3和模型8、9間隔中心截面速度沿高程變化
4 結論
以矩形柱模型簡化代替實際建筑模型,建立了10組并列建筑群的計算域,采用標準k-ε湍流模型進行數值模擬,對數值模擬結果進行對比分析,得出單體建筑物高度與并列建筑物高差對于間隔處周圍風場的影響是協調統一的.當單體建筑物越高,其對于間隔處風速的匯聚增幅作用越大,風速達到最大的高程越高.當相鄰建筑物高差越大,其風速增幅會相對降低,同時最大風速處高程也相對下降;單體建筑物高度與并列建筑物間距對并列建筑物周圍風場的共同影響.當間隔處間距過小時(D≤0.125H),風無法從間隔處正常通過.當單體建筑物高度適當(H≤40m)且不變時,間距大小與風速增幅成反比,且隨著間距的縮小,風速變化曲線會呈現不同的變化趨勢,但風速最終穩定在約為1.2倍的輸入風速.當間隔間距D≥0.125H,且建筑物單體高度增加到一定高度時(H≥60m),風速變化曲線就不再穩定于1.2倍輸入風速,而是隨高程增加而不斷減低,風速曲線成下降趨勢,最終達到與輸入風速.
[1] RYoshie,A Mochida,Y Tominaga,et al.Cooperative project for CFD prediction of pedestrian wind environment in the Architectural Institute of japan[J].Journal of wind Engineering and Industrial Aerodynamics,2007(95):1 551-1 578.
[2] B Blocken,J Carmeliet.Pedestrian wind conditions at outdoor platforms in a high-rise apartment building:generic subconfiguration validation,wind comfort assessment and uncertainty issues[J].Wind and Structures,2008(11):51-70.
[3] 呂文瑚,湯廣發,文繼紅.建筑數值風洞的基礎研究[J].湖南大學學報,1994,21(6):114-118.
[4] 馬劍,程國標,毛亞郎.基于CFD技術的群體建筑風環境研究[J].浙江工業大學學報,2007,35(3):351-354.
[5] 殷惠君,張其林,周志勇.標準低矮建筑 TTU 三維定常風場數值模擬研究[J].工程力學,2007,24(2):139-145.

