類鋰離子體系高角動量態1s2 ng(n=5 ～9)的精細結構的理論計算

韓雪飛，王 碩，邵 琳，荊 瑩，顧瑩瑩，徐 寧，胡木宏

(1. 遼寧師范大學物理與電子技術學院，大連116029;2. 遼寧省昌圖縣第四高級中學，鐵嶺112500)

1 引 言

目前，多電子原子結構和光譜特性與受控核聚變、等離子體科學、天體物理、放射性核束物理等領域中的許多重要的物理過程相關，其中高角動量態原子體系精細結構的理論計算和實驗研究備受關注. 對于多電子體系精細結構的理論計算，量子電動力學(QED)理論建立了精細結構哈密頓表達式，為高角動量態的精細結構理論計算奠定了基礎［1］. 具有1s2nl 殼層結構的類鋰原子體系是最簡單的多電子體系，對其精細結構進行準確計算和預言，對于揭示多電子原子內部電子之間相互作用規律、相關實驗數據的解釋以及多電子原子結構理論的豐富、發展等，都具有極其重要的意義.

近年來，全實加關聯方法已經系統地完成了高離化態1s2nl (n≤9，l≤3)能級結構和光譜特性的理論研究，積累了大量準確可靠的理論數據［2-6］. 本文將這種理論方法拓展應用到角動量較高的原子體系，計算了Z =9 ～20 類鋰原子體系高角動量態1s2ng (n =5 ～9)態的精細結構，取得了令人滿意的結果. 首先，在計算體系非相對論能量時充分考慮體系的各種物理效應和關聯，確定了體系的波函數;然后通過計算自旋-軌道相互作用和自旋-其他軌道相互作用的期待值得到了精細結構劈裂;最后考慮了量子電動力學效應和高階相對論效應對精細結構劈裂的貢獻，得到體系具有較高精度的精細結構理論計算結果.在計算過程中，本文采取的方法既充分發揮了組態相互作用方法在描述電子關聯效應方面的潛力，又克服了傳統組態相互作用方法所面臨的數值收斂慢的難題，完成了等電子序列Z =9 ～20 高角動量態1s2ng (n =5 ～9)態的精細結構的計算，得到體系精細結構劈裂沿等電子序列、Rydberg序列的變化規律. 目前，關于高角動量態離子的實驗數據較少，其精確度也不高，希望本文研究的理論結果能為相關的實驗研究提供有益的參考.

2 理論方法

本文采用平方可積解析的Slater 型基函數系，為了確保體系的波函數能夠充分描述電子之間的關聯效應，在保證理論計算高精度的前提下，波函數選取合理的項數，既能維持計算的穩定性，又克服了數值計算收斂慢的問題，極大的縮短了計算時間，體系波函數為:

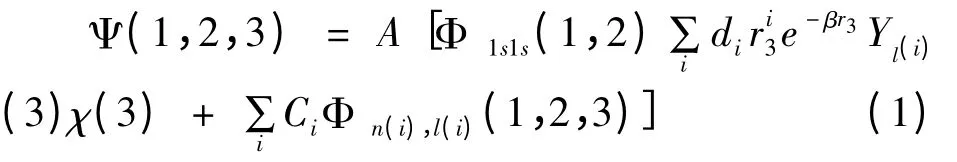
對于1s2nl (l ± 0)態，精細結構劈裂主要來源于自旋-軌道相互作用和自旋-其它軌道相互作用［7］，其中，自旋-軌道相互作用是最大的相對論效應，是精細結構的主要承擔者，在Breit -Pauli 近似下得到如下算符形式［8］:

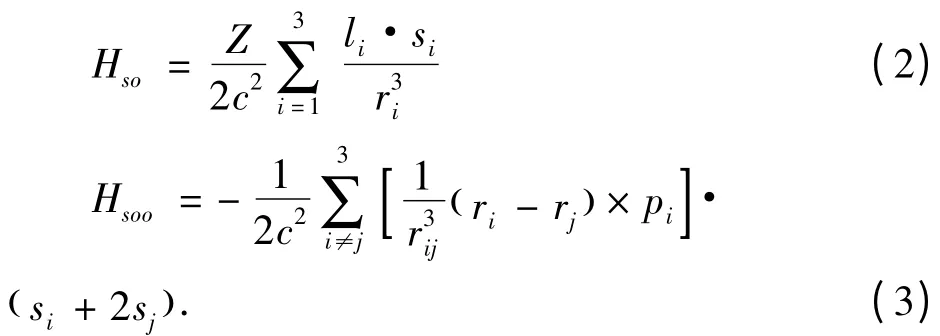
利用自旋-軌道相互作用算符和自旋-其它軌道相互作用算符在LS 耦合表象中波函數的期待值，得到體系1s2nl 態的精細結構劈裂:

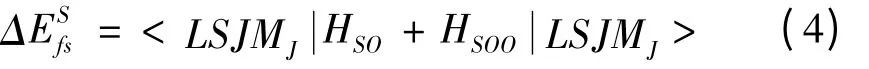
為了進一步得到高精度的理論計算值，利用類氫公式計算類鋰離子1s2nl 態的量子電動力學(QED)效應，它對精細結構劈裂的貢獻為［9］:

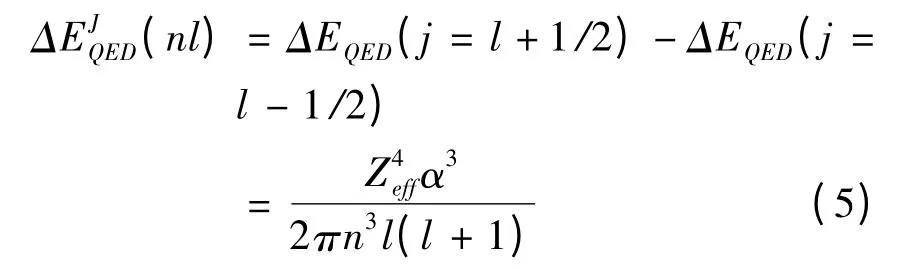
隨著核電荷數不斷增大，相對論效應的影響逐漸增強，因此需要考慮高階相對論效應對精細結構的貢獻. 引入有效核電荷的概念，根據庫侖勢的單電子Dirac 方程的能量本征值表達式，高階相對論修正為［10］:

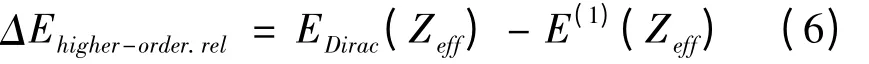
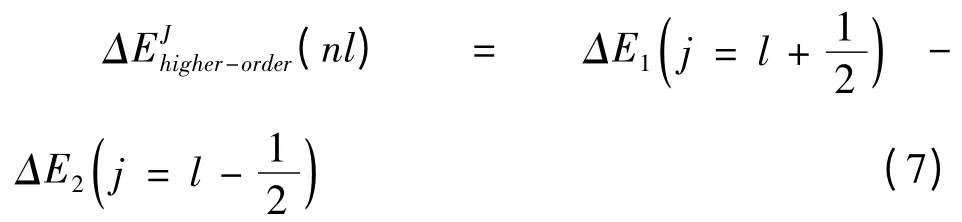
考慮以上各種修正后，原子體系總的精細結構劈裂表達式為:

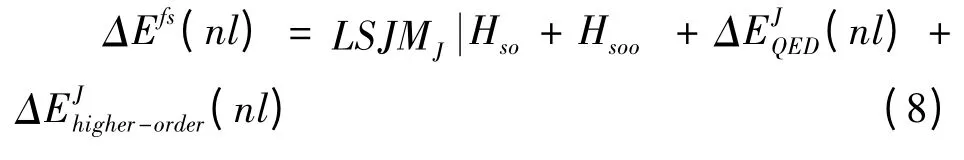
3 結果與討論

根據本文采取的理論方法計算得到的F6+高角動量激發態1s2ng (n =5 ～9)的精細結構劈裂結果見表1. 從表中可以看出，第二列的自旋-軌道、自旋-其它軌道導致的劈裂所占比重最大，例如1s25g 態的S. -O. +S. -O. -O. 值為5.6125 cm-1，占總劈裂的99.758%，其他效應對精細結構劈裂的貢獻占總劈裂的0.242%，其中高階相對論效應對精細結構劈裂的貢獻最小，僅為0.011 %，盡管QED效應和高階相對論修正對精細結構的貢獻并不十分明顯，但這些效應對于提高類鋰離子體系的精細結構劈裂理論計算結果的精度是非常重要的. 表2為計算得到的類鋰等電子序列Z =9 ～20 激發態1s25g 的精細結構，表3 為本文計算得到的類鋰等電子序列Z=9 ～20 高角動量態1s2ng (n =6 ～9)精細結構，從表中可以看出，自旋-軌道、自旋-其它軌道以及QED 效應和高階相對論效應對精細結構劈裂的貢獻都隨著核電荷數的增加而不斷增大，精細結構總劈裂也顯著增加，呈現與Z4eff成比例的規律，這完全符合導致精細結構的自旋軌道相互作用隨核電荷增大的變化規律［11］.

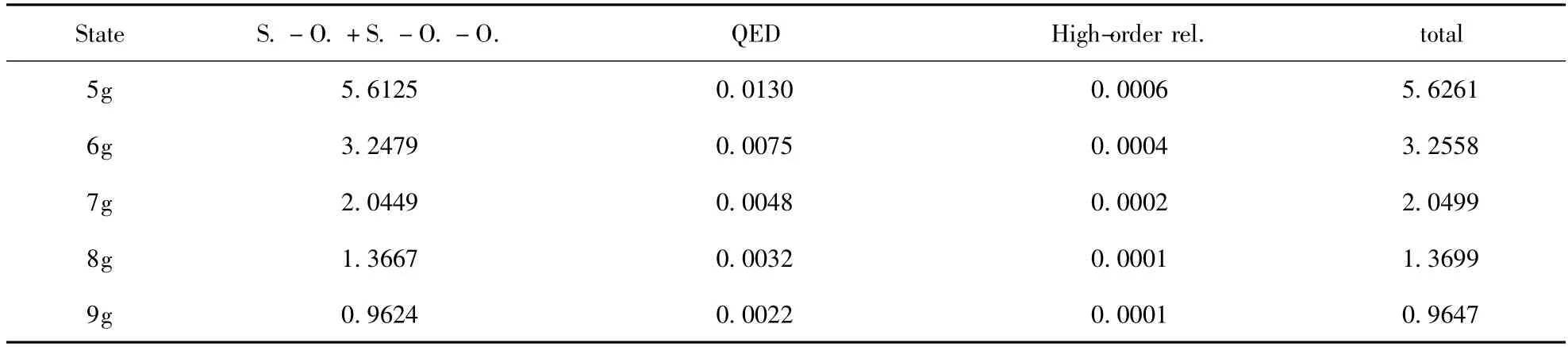
表1 F6+離子激發態1s2ng (n =5 ～9)的精細結構(cm -1)Table 1 Fine structure splittings for 1s2ng (n =5 ～9)states of lithium-like systems of F6+ (in cm -1)

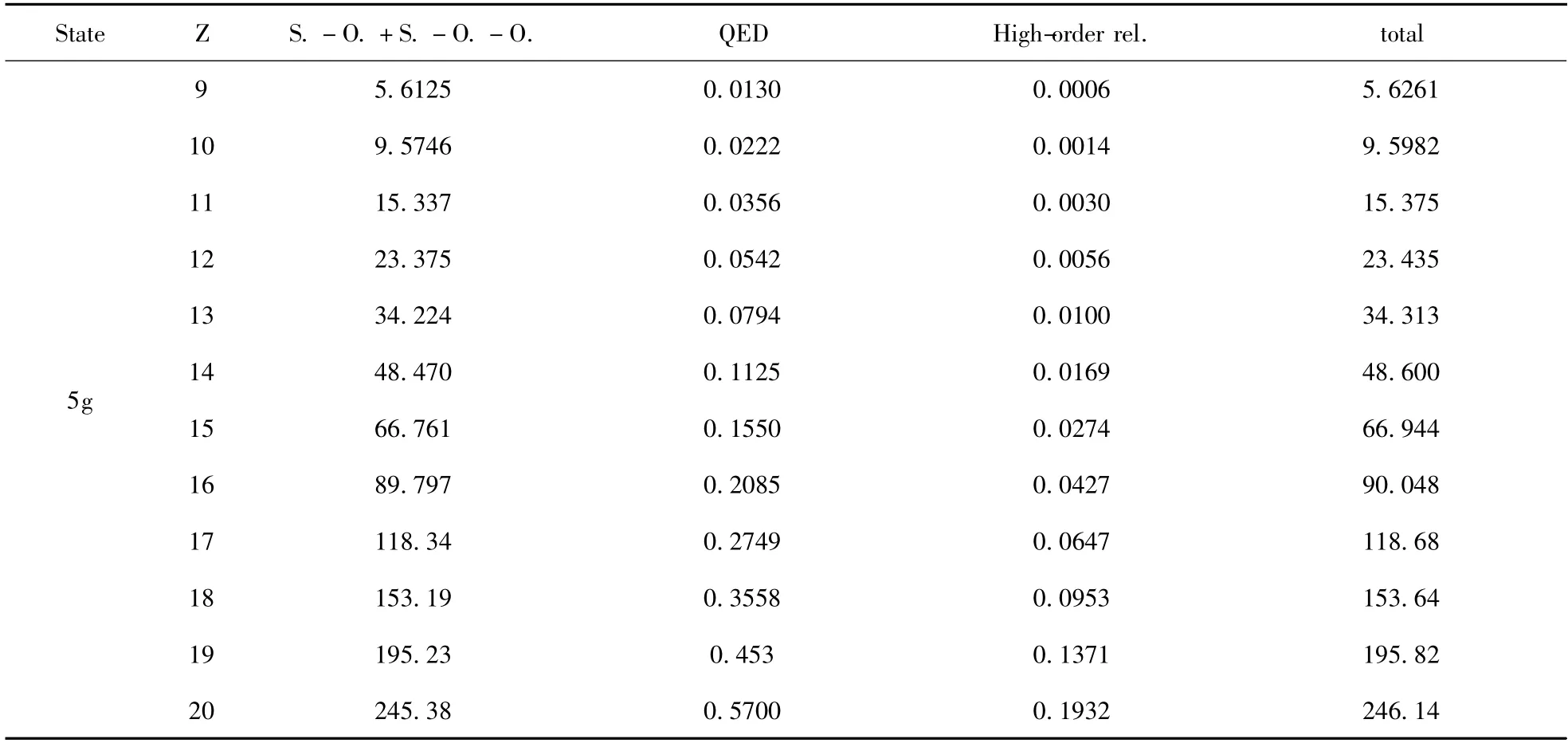
表2 類鋰等電子序列Z=9 ～20 激發態1s25g 的精細結構(cm -1)Table 2 Fine structure splittings for 1s25g states of lithium-like systems from Z=9 to 20 (in cm -1)

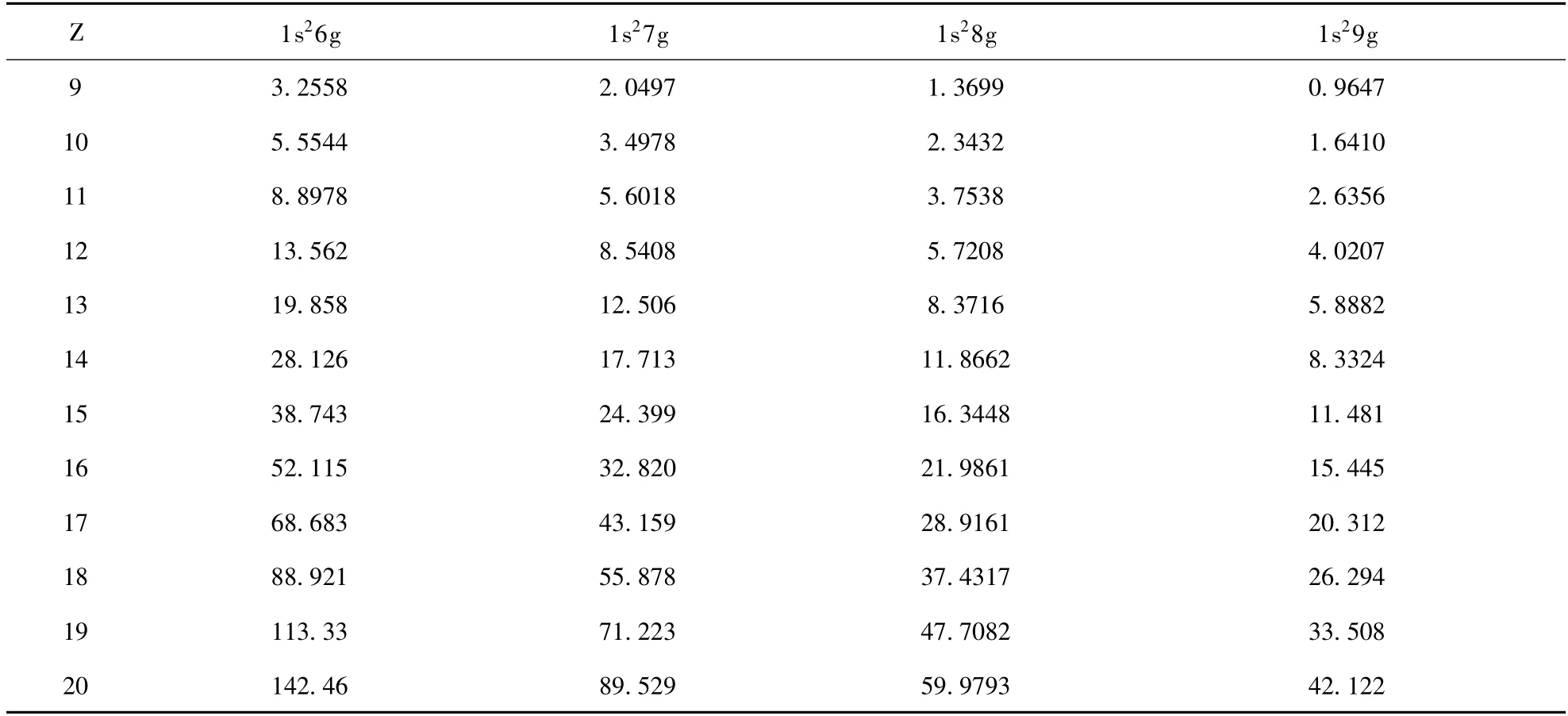
表3 類鋰等電子序列Z=9 ～20 激發態1s2ng (n =6 ～9)的精細結構(cm -1)Table 3 Fine structure splittings for 1s2ng (n =6 ～9)states of lithium-like systems from Z=9 to 20 (in cm -1)

圖1 和圖2 分別給出了精細結構劈裂隨著核電荷數Z 和主量子數n 的變化規律:隨著核電荷數Z 的增大，1s2ng (n =5 ～9)等電子序列的精細結構劈裂急劇增大，且增大率逐漸加大，如圖1;隨主量子數n 的增加，1s2ng (n =5 ～9)Rydberg 序列的精細結構劈裂越來越小，且趨于穩定，如圖2.

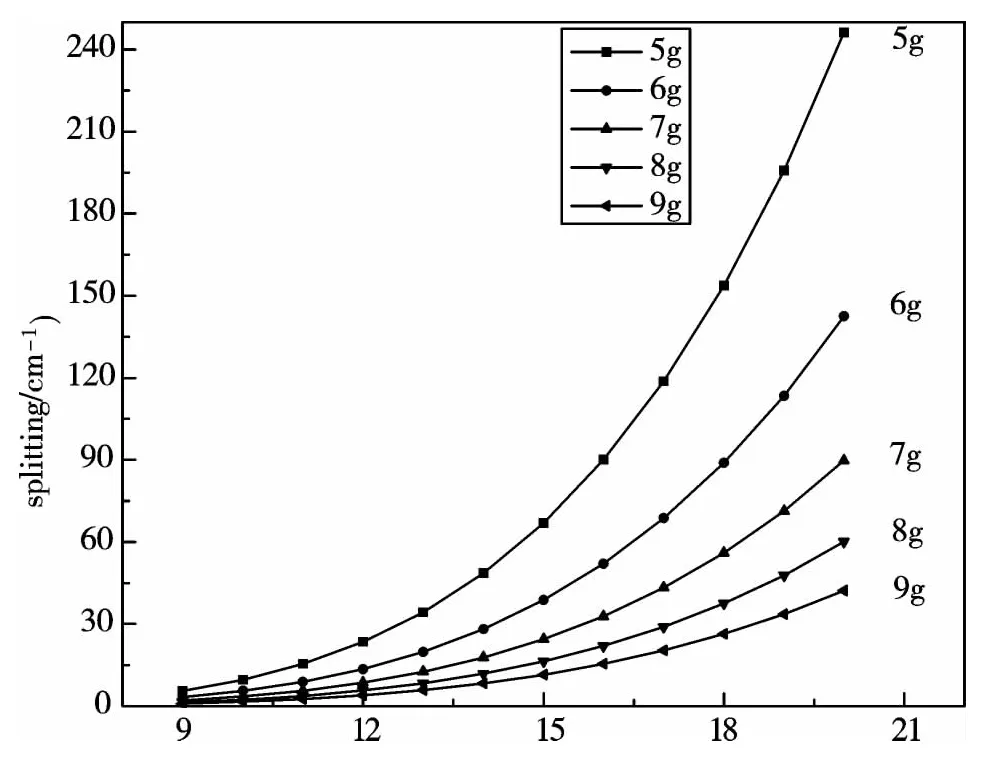
圖1 類鋰等電子序列1s2ng (n =5 ～9)精細結構劈裂隨核電荷數Z (Z =9 ～20)的變化關系Fig.1 Fine structure splittings of 1s2ng (n =5 ～9)states with the change of the nuclear charge Z (Z =9 ～20)

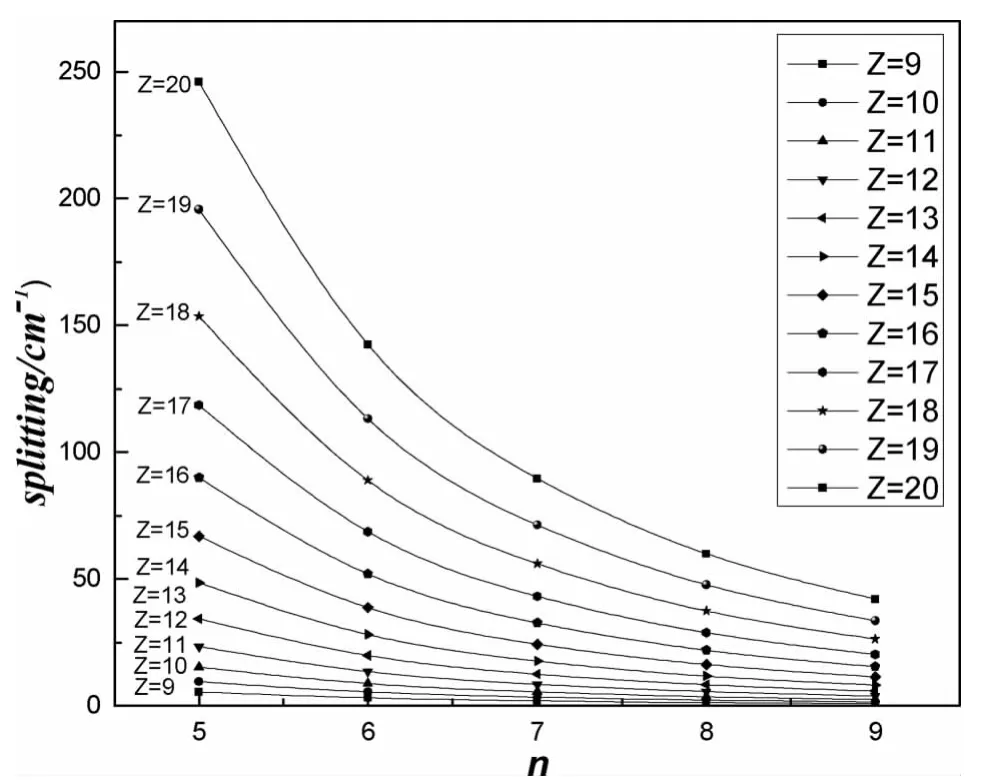
圖2 類鋰等電子序列1s2ng (5≤n ≤9)精細結構劈裂隨主量子數n (n =5 ～9)的變化關系Fig.2 Fine structure splittings of 1s2ng (5≤n ≤9)states with the change of the principal quantum n (n =5～9)

4 結 論

由于實驗數據和其它理論計算結果極少，本文的理論計算結果還有待于實驗數據和其他方法的進一步檢驗，但本文得到結果完全符合精細結構變化的物理規律. 計算所得的精細結構劈裂值具有很好的等電子序列規律性，而且核電荷數較大的體系，精細結構變化比較顯著. 相信本文的理論結果對于相關的實驗研究和彌補現有數據的不足具有參考價值，同時也希望本文計算得出的數據與高精度的實驗相結合，為高角動量態的能級結構和光譜特性的數據完善提供一些理論依據.

［1］ Huang S Z，Wang D L，Huang W X. Derivation of the fine structure hamiltonian for multi-electron atoms by QED［J］. J. At. Mol. Phys. (原子與分子物理學報)，2003，20(2):233 (in Chinese)

［2］ Liu X，Wang Z W，Liu B H，et al. Fine structure and dipole oscillator strength of Zn27+ion［J］. J. At. Mol.Phys. (原子與分子物理學報)，2008，25(5):1045(in Chinese)

［3］ Wang Z W，Liu Y，Hu M H，et al. Transition energy and dipole oscillator strength for 1s22p - 1s2nd of Cr21+ion［J］. Chin. Phys.，2008，17(8):2909.

［4］ Wang Z Z，Guo Y. Fine structure of 1s2np state for Ni25+ion［J］. J. At. Mol. Phys. (原子與分子物理學報)，2009，26:597(in Chinese)

［5］ Hu M H，Wang Z W. Oscillator strengths for 22S-n2P transitions of the lithium isoelectronic sequence from Z=11 to 20［J］. Chin. Phys. B，2009，18(6):2244.

［6］ Hu M H，Wang Z W，Zeng F W，et al. Energy levels of 1s2nd(n≤9)states for lithium-like ions［J］. Chin.Phys. B，2011，20(8):083101.

［7］ Konschuh S，Gmitra M，Kochan D. Theory of spin-orbit couplingin bilayer graphene ［J］. Phys. Rev. B，2012，85:115423.

［8］ Bethe H A，Salpeter E E. Quantum mechanics of oneand two-electron atoms［M］. Berlin:Springer-Verlag，1957:178 -183.

［9］ Yerokhin V A，Pachucki K A，Harman Z A，et al.QED theory of the nuclear magnetic shielding in hydrogenlike ions［J］. Phys. Rev. Lett.，2011，107(4):043004.

［10］ Chung K T. Ionization potential of the lithium like 1s22s states from lithium to neon［J］. Phys. Rev. A，1991，44:5421.

［11］ Kelly R L. Atomic and ionic spectrum lines below 2000 angstroms:Hydrogen through Krypton Part 1(HCr)［J］. J. Phys. Chem. Ref. Data，1987，16:1.