車道占用對道路通行能力的影響研究

陸 霞，楊李娜，王華棟，嚴傳魁

（杭州師范大學 理學院， 浙江 杭州 310036）

車道占用對道路通行能力的影響研究

陸 霞，楊李娜，王華棟，嚴傳魁

（杭州師范大學 理學院， 浙江 杭州 310036）

本文通過某路段交通事故發生后的情況，研究不同車道被占后道路橫斷面實際通行能力的變化，得出路段不同情況下排隊長度達到上游路口所需時間，同時估算車道被占用對城市道路通行能力的影響程度，為交通管理部門正確引導車輛行駛、審批占道施工、設計道路渠化方案、設置路邊停車位等提供理論依據.

多項式擬合；方差；排隊論；M/M/S/∞ 模型；Matlab 仿真

伴隨著經濟社會的發展，城市道路交通流密度越來越大，交通事故發生率持續升高，車道數、車道寬度、沿線街道化狀況、交通量大小、混合車種及外界環境等因素都會影響城市道路通行能力.大量研究者致力于道路通行能力的問題，如胡耀增，李楊，林晨[1]研究了車流量的交通信號燈控制模式和仿真，裝備制造技術對道路通行能力的影響；宋延，周偉，孫姝婷[2]等，研究了多相位信號交叉口通行能力評估方法；高旺生，涂輝招，杜豫川[3]等，研究了一種新的城市道路通行能力計算方法——等效通行能力法；施娟，孔令江，劉慕仁[4]研究了紅綠燈控制下的交通波.這些研究對城市道路通行能力的評估、信號燈對道路通行能力的影響做了理論上的計算，而對于具體事故發生后的道路通行能力涉及較少.本文選擇 2013年全國大學生數學建模競賽 A題的視頻材料，研究基于路段交通事故發生后的擁堵排隊問題.

1 車輛排隊長度相關因素分析的模型建立與求解

假設車輛到達率服從泊松分布.用 spss對到達的車輛數據進行泊松分布檢驗，證實了進入上游路口的車輛到達率確實服從泊松分布.驗證結果如表1.

車輛到達系統的相繼到達時間間隔獨立，且服從參數為 λ 的負指數分布 (即輸入過程為過程），服務臺的服務時間也獨立同分布，且服從參數為μ的負指數分布.所以采用等待制排隊模型中(M/M/S/∞)模型.

根據 lingo編程可知，車輛等待的概率：

Pwait=@peb(load,S).

該函數為 Lingo內部函數，返回值是當到達負荷為 λT，系統中有 S個服務臺且允許排隊時系統繁忙的概率，也就是車輛等待的概率.

車輛的平均等待時間：

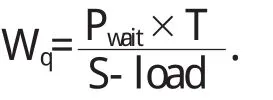
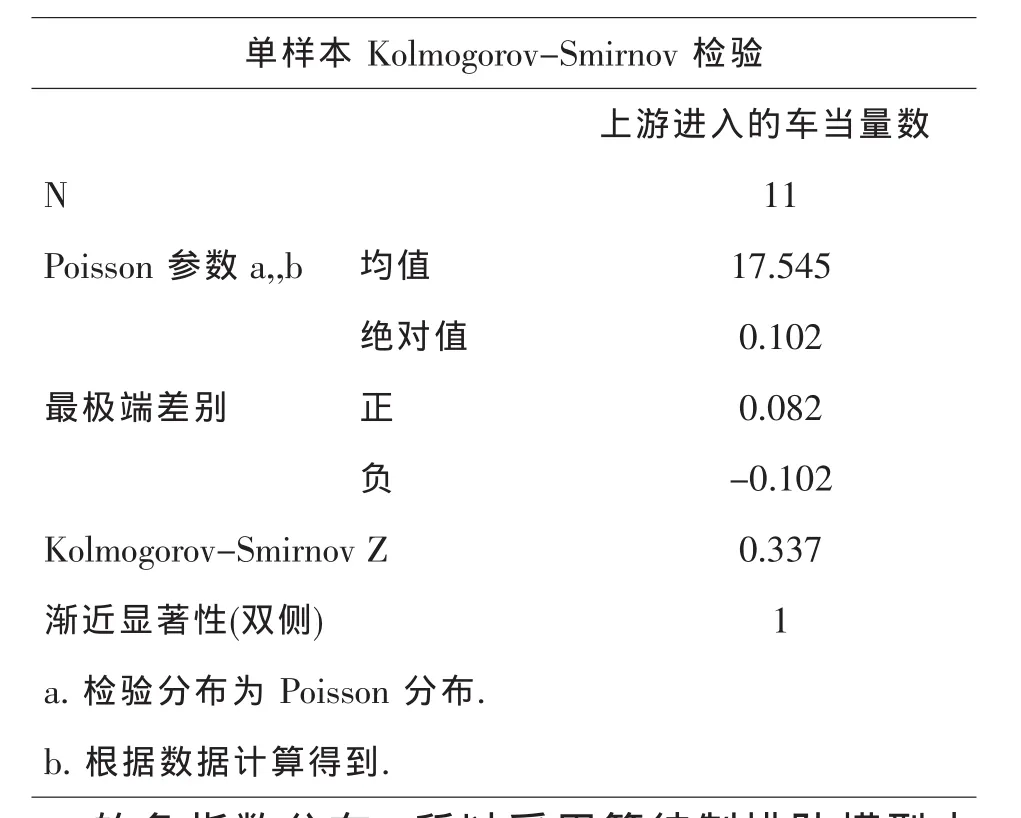
表1 單樣本 Kolmogorov-Smirnov檢驗

車輛等待隊長：Lq=λWq=RWq

利用已建立模型，求解車輛等待隊長為 39米，而理想排隊車長為 40.83米，發現誤差僅為 4.4%，說明本模型可用.

2 車輛排隊長度將到達上游路口所需時間

采用排隊論與模擬仿真的方法來解決車輛排隊長度到達上游路口所需時間問題.排隊現象的要素包括兩個方面的內容：一是通過車禍橫斷面的車輛；二是事故現場車輛可通過的車道數.排隊系統形式如圖1：

圖1 交通事故排隊系統形式

采用面向對象的仿真方法，選取事件發生時刻為仿真時鐘 0.由于 Matlab中的計算均為矩陣計算，故利用矩陣形式建立事件參數表 events，矩陣events的行表示車輛的不同參數，列表示不同的車輛.針對 M/M/1/N/∞ 模型的特點，建立車輛信息如下表所示.

表2 車輛信息表

首先進行車輛信息初始化.根據到達率λ和交通事故橫段面平均放行率μ，確定每個車輛的到達上游路口的時間間隔和車輛的通過事故橫斷面的時間間隔.由此確定每個車輛的到達上游路口時刻.在 Matlab仿真中，用函數 cumsum（x）實現累加功能，選取 10分鐘作為仿真時間.

再對當前車輛進行初始化.第 1個到達系統的車輛不需要等待就可以直接接受服務，其離開時刻等于到達時刻與車輛通過事故橫斷面所花費時間服務時間之和.最后，對標準車當量數統計分析，代入數據和分析可得：

車輛到達率

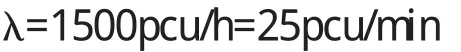
車禍橫段面平均放行率

μ=21pcu/min

等待車輛數最大值

在以上分析的基礎上，利用 MATLAB進行仿真編程.假設各顧客的到達時間間隔和服務時間均服從負指數分布.

平均到達時間 =1/橫段面到達率；

平均放行時間 =1/橫段面平均放行率.

根據上述結果，仿真得到圖 2：

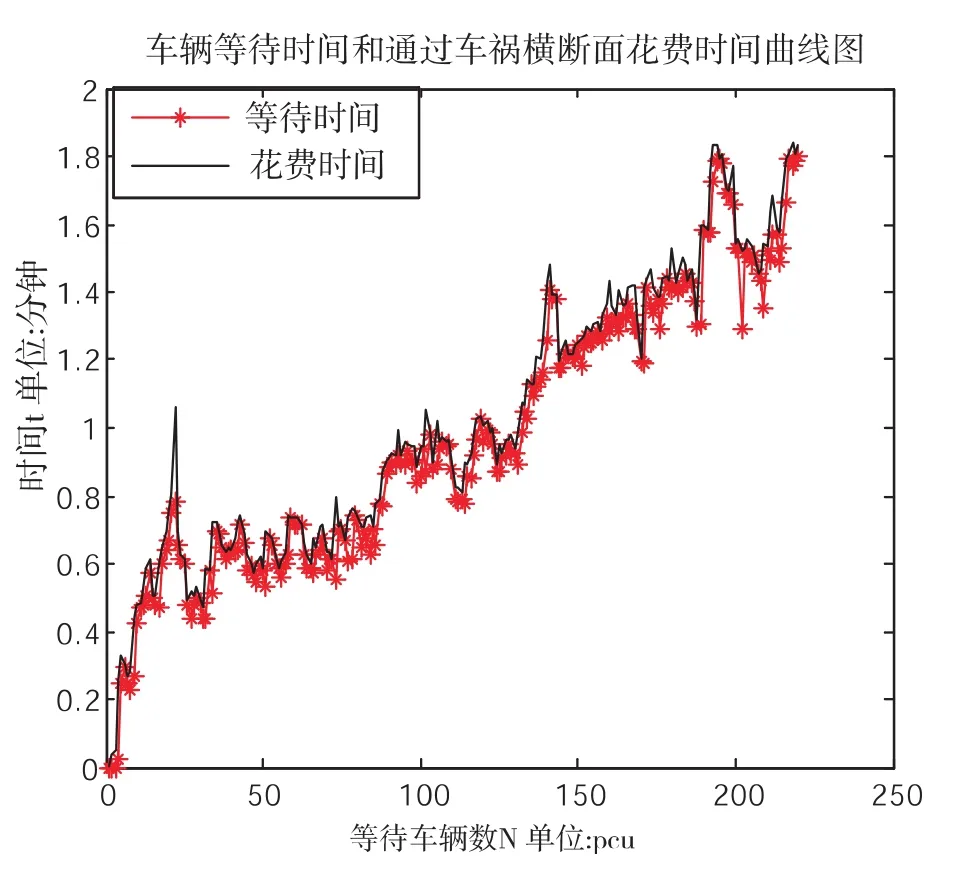
圖2 車輛等待時間與服務臺服務時間

通過圖 2發現，等待車當量數與交通事故所導致的等待時間基本成正比，且由于車通過橫斷面的時間相對極短，車輛等待時間曲線與事故橫斷面花費時間曲線基本重合.

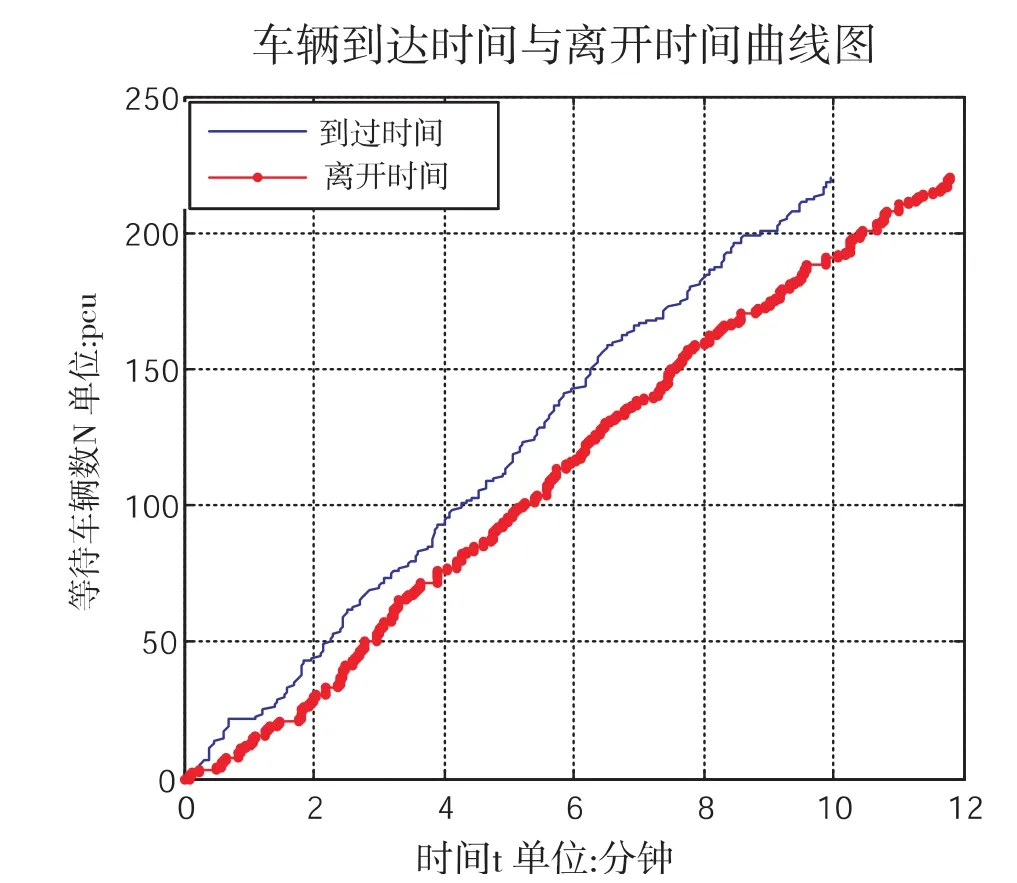
圖3 車輛到達時間與離開時間曲線圖

分析圖3可得：

（1）在發生車禍后到達上游路口的車輛的等待車輛數隨著車禍時間的推移而增長，發生車禍后到達上游路口的車輛的的時間越晚，等待車輛數越多，排隊長度越長.這是由于車禍發生后，車禍橫斷面的實際通行能力下降，車輛到達上游路口的到達率有 25pcu/min，但是通行量不等于到達率.當通行量小于到達率時，車輛就會堆積，排隊隊伍就會變長.

（2）在 1.5分鐘內，到達時間與離開時間兩條曲線差距較小，也即在發生車禍后 1.5分鐘內到達上游路口的車輛的到達時間與離開時間的差值較小，這說明了車輛所需的排隊時間也較短.1.5分鐘后，到達時間與離開時間兩條曲線差距較大，車輛到達時間與離開時間的差值增大，排隊時間也相應增加.

（3）在 2.2分鐘左右，到達時間與離開時間的差值大致等于 28pcu，也就是達到了等待車輛數的最大值 28pcu.若 3條車道的等待車輛都達到最大值，則需要時間為 2.2的 3倍，也就是 6.6分鐘.

也就是從事故開始，經過 6.6分鐘，排隊長度就達到了 140米，車輛排隊長度將到達上游路口.

由于上模型考慮三車道等待車輛達到上游路口時所需時間是在單車道的基礎上乘以一定的倍數得到的，存在誤差較大.在原有模型的基礎上，根據不同道路類型多車道設計通行能力進行了模型改進.

表3 不同道路類型多車道設計通行能力

根據表3，得出單車道修正系數為1，三車道為2.67.例如，在單車道中，以通過上游橫斷面為例.通過單車道，假設以 10pcu標準車當量的車為堵車上限，將通行能力定為標準量 1輛 /秒，則 10pcu標準車當量的車通過的時間為 10/1=10秒,同樣情況在三車道中，則堵車上限為 30pcu標準車當量的車，車道的通行能力為 2.67pcu/s，則 30pcu標準車當量的車通過的時間為 30/2.67=11.24秒，所以三車道的時間為一車道的 1.24倍.根據 matlab仿真得到的堵塞 140米單車道的時間為 2.2min.

故堵塞 140米三車道的時間

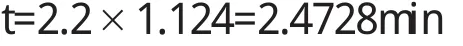
3 結論

根據上游紅綠燈周期車流量分析確定其滿足泊松分布，建立排隊論模型.在排隊論M/M/S/∞模型基礎上，根據已知上游車流量，橫斷面距上游路口距離等條件，利用 Matlab仿真得到車輛到達時間與離開時間關系曲線圖，得到經過6.6分鐘，排隊長度就達到了 140米，車輛排隊長度將到達上游路口.同時考慮了三車道與單車道堵車時間并非純線性關系，通過比例轉換得到三車道隊列達到上游路口所需時間為 2.4728分鐘.最后給出了滿足一定條件的基于以上模型設計的車道被占用后對道路通行能力的影響.

〔1〕胡耀增，李楊，林晨.車流量的交通信號燈控制模式和仿真[J].裝備制造技術，2012（11）:17-18.

〔2〕宋延，周偉，孫姝婷，等.多相位信號交叉口通行能力評估方法[J].交通科技,2010(9).

〔3〕高旺生，涂輝招，杜豫川，等.一種新的城市道路通行能力計算方法——等效通行能力法 [J].交通工程,2005(1).

〔4〕施娟，孔令江，劉慕仁.紅綠燈控制下的交通波[J].廣西師范大學學報,2002,20（3）.

O29

A

1673-260X（2014）08-0001-03

杭州師范大學攀登工程數學建模子項目