基于盒維數的保持架質心軌跡穩定性分析
譚晶,儲著金,顧志鑫,梁建波
(上海大學 機電工程與自動化學院,上海 200072)
保持架的動態特性是球軸承動力學性能中一個極為重要的方面。保持架渦動等不穩定的保持架運動會導致軸承嘯叫并使摩擦力矩產生較大波動。因此,研究保持架的動態特性對于改進軸承設計、提高軸承壽命具有十分重要的意義。
表面波紋度一直是評價球軸承幾何特性的重要參數,雖然國內外對保持架的動力學特性都有較為深入的研究,但有關表面波紋度對保持架動態特性影響的相關報道卻很少。文獻[1]利用ADAMS對滾針軸承保持架進行了動力學仿真,利用模態綜合法分析了保持架的動態應力分布,但并未提及保持架的運動特性。文獻[2]利用離散單元法分析了柔性保持架的動態特性,重點對比了與剛性保持架動態特性的差異。文獻[3-4]對保持架的擬動力學特性進行了理論分析。文獻[5-8] 利用ADAMS討論了保持架的動態特性,得到了許多有益的結論。文獻[9]討論了表面波紋度對保持架質心軌跡穩定性的影響,但缺乏對保持架質心軌跡優劣的定量描述。下文提出用盒維數定量評價保持架質心軌跡的混亂程度,并通過建立多體動力學模型分析表面波紋度對保持架質心軌跡的影響規律。
1 基本理論
1.1 表面波紋度理論模型
由于制造誤差,軸承內、外圈溝道表面和鋼球表面等都不是幾何真圓,不同程度地存在圓度誤差,這些誤差又是隨機的,在圓周方向上呈波譜狀展開。
軸承溝道表面波紋度的幾何曲線r用極坐標可表示為
r=r0+yi,
(1)
yi=Δrsin(360nt+β),
(2)
式中:r0為內、外圈溝道半徑;Δr為軸承溝道表面波紋度最大諧波幅值;β為初始相位角;n為軸承溝道表面波紋度的諧波階次,n=2πr0/λ,λ為波長;t為介于0與1之間的常數。
軸承制造誤差,如表面波紋度在旋轉過程中會引起周期性的接觸變形,運用所建立的振動模型可以分析表面波紋度激勵產生的軸承振動。表面波紋度存在于內、外溝道或鋼球上,其模型如圖1和圖2所示。
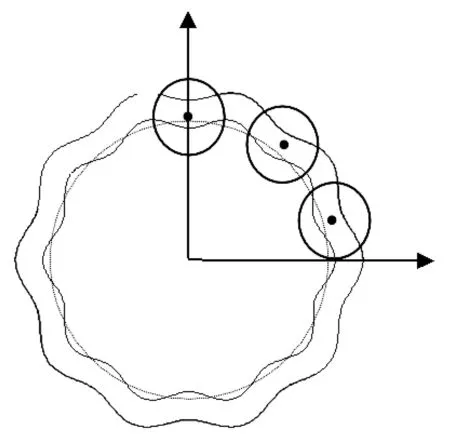
圖1 內、外圈表面波紋度模型
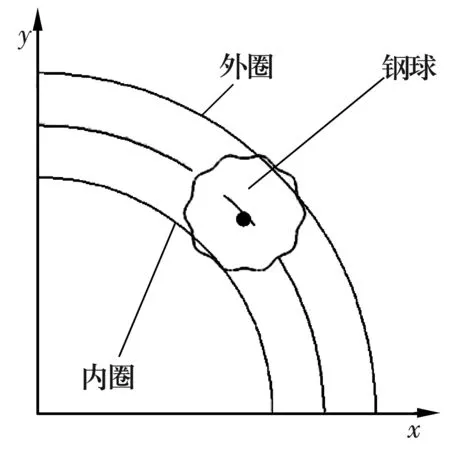
圖2 鋼球表面波紋度模型
1.2 盒維數
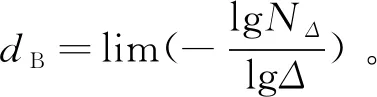
目前,保持架動態特性的優劣主要通過人為觀察來判定,缺少評價的客觀性。而且當保持架質心軌跡較為復雜時,通常變得難以評定。故根據盒維數的計算原理,通過MATLAB編程,分析二維數字圖像,以客觀評價保持架質心軌跡的復雜程度,為定量觀察保持架的動態特性提供借鑒。此方法的優點是既有圖像處理又有數值分析。
2 仿真結果與分析
2.1 仿真工況與邊界條件
以7003C角接觸球軸承為研究對象,在ADAMS中建立參數化模型。首先進行內圈的參數化建模,創建如圖3所示的變量(design variable)。圖中B為內圈寬度;l為內圈一側到內圈溝道中心的距離;ri為內溝曲率半徑;F為內溝道直徑;d為軸承內徑;d1為內圈外徑。最后建立的內圈參數化模型如圖4所示。

圖3 內圈參數

圖4 內圈模型
根據所用實體保持架的尺寸,建立保持架的設計變量如圖5所示。需要注意的是,保持架具有均勻分配的圓孔,圓柱體在旋轉時的計算公式為90.0+360n/Z,其中,n=1,2,…,Z(Z為鋼球數),保持架材料為酚醛夾布。建立的外圈設計變量如圖6所示。在建立外圈擋邊傾斜角β部分時,要注意的是圓錐體大端半徑為E/2,小端半徑為E/2-(C-h)tanβ。
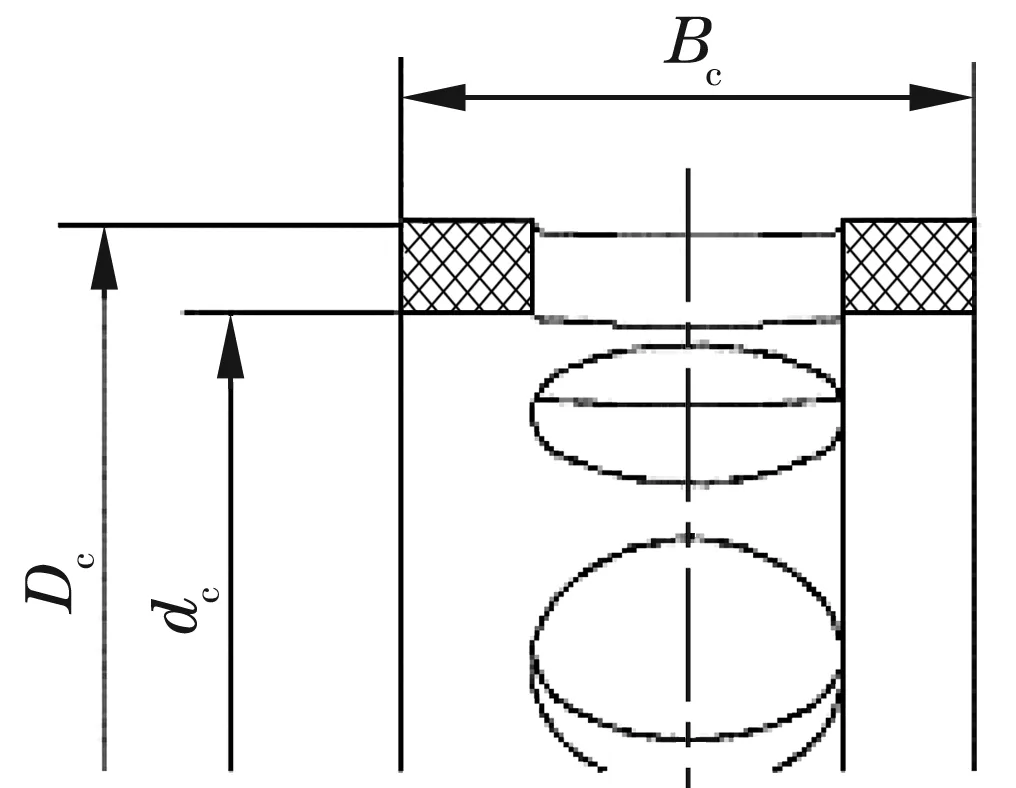
圖5 保持架參數

圖6 外圈參數
建立鋼球的參數化模型時,也要與保持架兜孔相對應,注意球的位置,并使用旋轉公式。建立的軸承參數化模型如圖7所示。建模后可按照設定的設計目標,修改某些參數即可對不同軸承模型進行仿真計算,可大大提高運算效率,減少重復勞動。

圖7 軸承參數化模型
軸承外圈固定,內圈以n=1 800 r/min定速轉動,同時內圈承受徑向載荷Fr=50 N,軸向載荷Fa=200 N。設仿真時間為1 s,仿真步數為1 000,觀察保持架在垂直于軸線方向平面內質心的運動軌跡。
2.2 外溝道表面波紋度諧波階次和球數的影響
設定表面波紋度諧波幅值Δr=2 μm,當表面波紋度位于外溝道,其他零件為理想真圓時,針對球數為13,12,11的3種結構,分別對表面波紋度諧波階次n=4,5,…,15時的不同情況按照給定工況仿真后得到保持架的質心軌跡。根據盒維數原理,進行MATLAB編程,然后將ADAMS分析得到的保持架質心軌跡數據導入程序,應用MATLAB程序計算質心軌跡的盒維數,得到外溝道不同表面波紋度諧波階次下保持架質心軌跡的盒維數。
不同球數時,保持架質心軌跡盒維數隨外溝道表面波紋度諧波階次的變化規律如圖8所示。由圖可知:(1)隨著表面波紋度諧波階次的增加,保持架質心軌跡的復雜性趨于平穩;(2)表面波紋度的諧波階次為7時,保持架質心軌跡的復雜性有明顯波動;(3)當外溝道表面波紋度的諧波階次相同時,隨著球數的減少,質心軌跡的混亂程度呈增加趨勢。

圖8 保持架質心軌跡盒維數隨表面波紋度諧波階次及球數的變化規律
2.3 不同零件表面波紋度的影響
為研究不同零件表面波紋度對保持架質心軌跡的影響,分別計算外溝道、內溝道及鋼球的表面波紋度諧波階次為4時保持架質心軌跡的盒維數,結果如圖9~圖11所示。仿真過程中,給定的鋼球數為12,表面波紋度的諧波幅值Δr=2 μm。
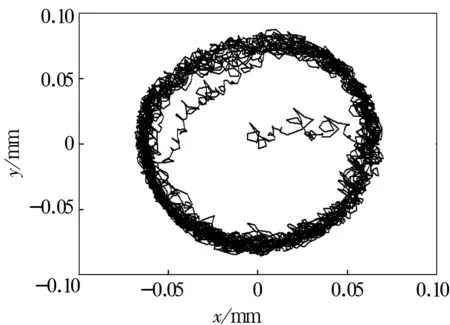
圖9 表面波紋度位于外溝道(盒維數值1.490)
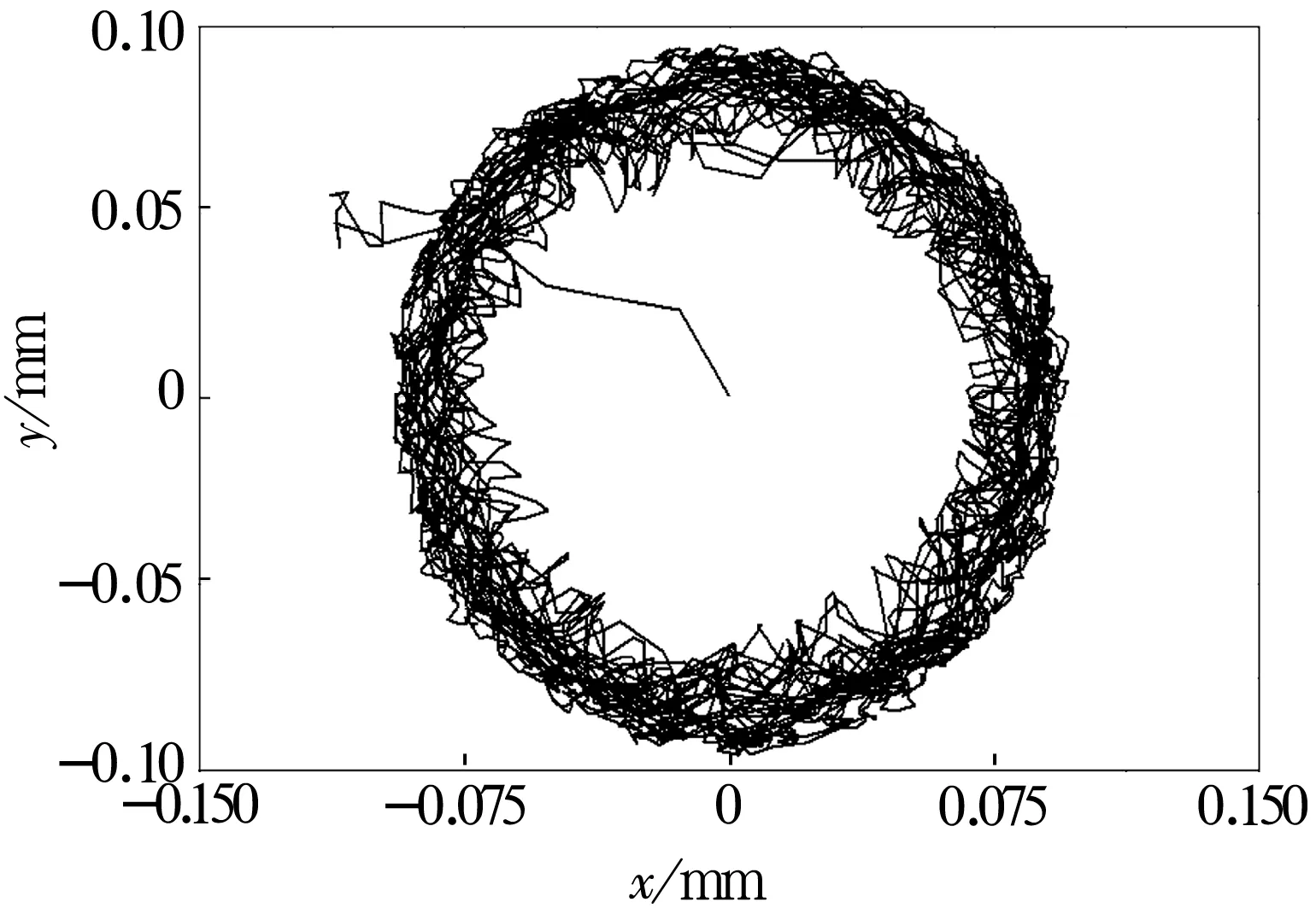
圖10 表面波紋度位于內溝道(盒維數值1.494)
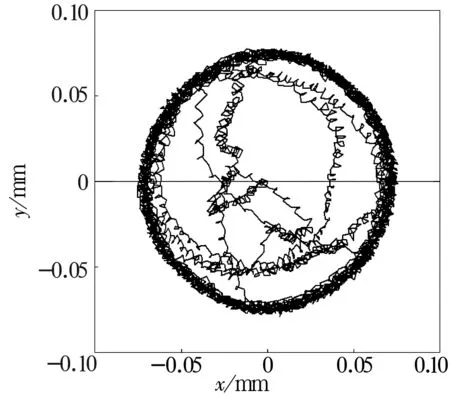
圖11 表面波紋度位于鋼球表面(盒維數值1.499 6)
由圖中的盒維數值可以看出,當表面波紋度位于鋼球表面時,保持架質心軌跡最為混亂,故可以認為,鋼球表面波紋度對保持架質心軌跡的影響程度最大;內溝道表面波紋度次之,而外溝道表面波紋度影響最小。此結果可以為制定軸承零件加工工藝提供一定的借鑒,相對于內、外圈來說,提高鋼球表面的形狀誤差可以更好地改善保持架質心軌跡。
3 結束語
仿真和計算結果表明,表面波紋度的諧波階次、球數及表面波紋度所處的位置均對保持架質心軌跡有較為顯著的影響。
生產中外圈表面波紋度是不可避免的形狀誤差,但應盡量提高其諧波階次。增加球數可以平穩保持架的質心軌跡,相對于外溝道而言,改善鋼球和內溝道的形狀誤差能夠更加有效地控制保持架質心軌跡的復雜性。

