CORDIC算法原理

曹劍英，劉凌云

（集寧師范學院 物理系，內蒙古 烏蘭察布 012000）

CORDIC算法原理

曹劍英，劉凌云

（集寧師范學院 物理系，內蒙古 烏蘭察布 012000）

CORDIC算法根據不同的旋轉軌跡分成線性系統、圓周系統和雙曲系統；每個系統又有旋轉模式和向量模式兩種，本文詳細地來闡述CORDIC的算法原理和實現不同的運算，給初學者一些參考.

坐標旋轉算法；CORDIC算法；原理

1 CORDIC算法原理

1.1 算法推導[1]

圖1 平面坐標的旋轉

CORDIC算法是一種旋轉坐標的方法.設起點坐標為P0=(x(1),y(1))，旋轉θ角度，得到終點坐標，設為Pn=(x(2),y(2))，如圖1所示.由三角函數知識，旋轉后的坐標由式（1-1）計算得到(1-1)

其中

即

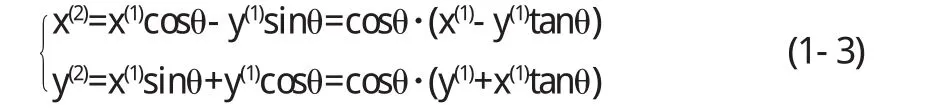
矩陣R可以寫成

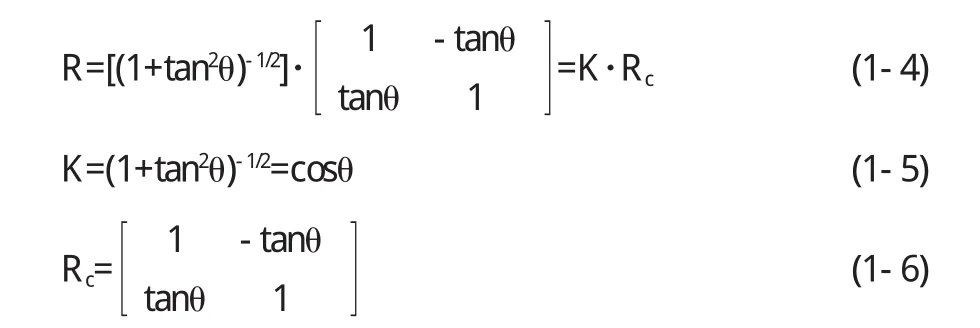
這樣，設P'n=Rc·P0，則

把cosθ去掉后相當于把旋轉后矢量的模減小了，為了保證最終的結果正確，一般在結果的后面乘上一個系數K.對于某一個角度β，假定初始角度為z0，可以通過z0經過若干個小角度θi的旋轉獲得

并可以得到如下所示的迭代公式：

假設我們從X軸開始旋轉，通過一些列逐次減少的角度旋轉后，只要迭代的次數足夠多，就可以實現內任意角度的旋轉，并且通過加法和移位運算得到目的的橫坐標和縱坐標.每次旋轉后得到的實際矢量和目標矢量之間的誤差角度（目標角度減去實際角度）如下式：

其中，z0為目標矢量角度，若zi<0，則di=1.實際迭代后累計角度為：

其中a0=0.例如，要實現680的矢量旋轉，我們可以列出第i次對應的旋轉角度、旋轉方向、迭代后的實際角度和誤差如表1所示.

表1 旋轉680的CORDIC實現

一旦zi迭代的次數確定了，∏Ki也就確定了，Ki的乘積可以在實現時不做處理，而是被當做整個系統處理增益的一部分，實際的增益取決于迭代次數n.

當n趨于無窮大時，An的極限值約為1.647.在實現CORDIC算法時，由于An當作系統的處理增益不做處理，因此只需要移位、相加運算就可完成矢量旋轉，很適合在FPGA中實現[2].

2 CORDIC算法引申及模型

以上所作的Cordic理論分析，只是Cordic算法提出時的理論雛形；之后，John Walther于1971年對其進行了擴展引申，進一步的完備了Cordic算法，得到以下Cordic的迭代模型[2].

這里，

i表示迭代索引（比如i=1,2,…,N），δi=+1 -｛1視情況而定.

根據m=1,-1,0，分別稱為圓周旋轉運算（Circular）、雙曲旋轉

運算(Hyperbolic)和線性旋轉運算(Linear)，也即

根據δi取值的判讀方式，CORDIC算法又分為旋轉模式和向量模式.

2.1 向量模式

設初始旋轉的角度為z0=θ，經過N次旋轉后，使得yN=0，這時

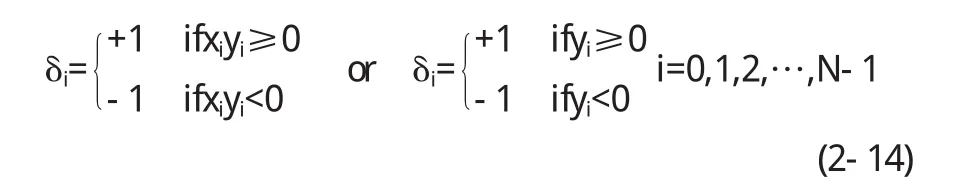
這樣的模式稱為向量模式.根據式（2-11），可得迭代N次之后，有

這里f(x,y,z)、g(x,y,z)表示某具體的函數，比如兩變量的乘法除法運算，具體是哪類函數，還需要根據式（2-13）中的m取值而定.

2.2 旋轉模式

設初始旋轉的角度為z0=θ，經過N次旋轉后，使得zN=0，這時

這樣的模式稱為旋轉模式.根據式（1-10），可得迭代N次之后，有

這里f(x,y,z)、g(x,y,z)表示某具體的函數，比如正弦余弦函數，具體是哪類函數，還需要根據式（2-13）中的m取值而定.

2.3 線性CORDIC

當式（2-13）中的m取值為0時，對應的是線性運算模式下的CORDIC算法.將m=0代入式（2-11），則得到如下迭代式

其中，根據式（2-12），得到θi的計算式，如下

對于初始變量x0,y0,z0，限制性條件為

由式（2-20）可知，在滿足式（2-21）的條件下，輸入z0=0，則可以迭代實現兩變量的除法操作.

在旋轉模式下，zi+1→0，迭代N+1次后，得到如下的結果

對于初始變量x0,y0,z0，限制性條件為

由式（2-22）可知，在滿足式（2-23）的條件下，輸入y0=0，則可以迭代實現兩變量的乘法操作.

2.4 圓周CORDIC

當式（2-13）中的m取值為1時，對應的是圓周運算模式下的CORDIC算法.將m=1代入式（2-11），則得到如下迭代式

i=0,1,2,…,N是迭代次數.

在向量模式下，yi+1→0，迭代N+1次后，得到如下的結果

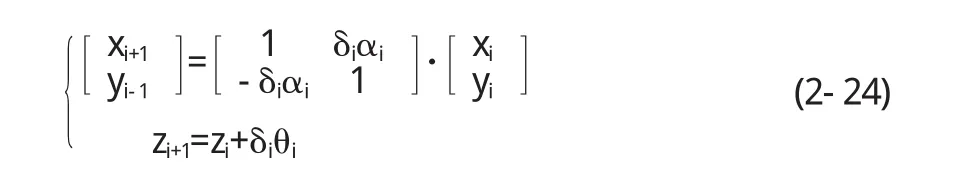
其中，θi=arctan2-i，αi=2-i，i=0,1,2,3,…,N是迭代次數.

在向量模式下，y→0，輸入值yin,xin的限制條件是|atanh (yin/xin)|≤1.7433(99.90)，迭代結果為

在旋轉模式下，x→0，輸入zin的限制條件是|zin|≤1.7433(99.90)，得到的迭代結果為

這里所能表示的角度范圍是在-99.90～99.90，在計算不在這個范圍角度值的三角函數值，需要進行預處理.進行預處理也是一個比較可行的方法，但是，這會較大程度上加大設計的復雜度[3].

2.5 雙曲CORDIC

雙曲模式下，m=-1，得到的迭代式是：

其中，θi=arctan2-i，αi=2-i，i=0,1,2,3,…,N是迭代次數.

在向量模式下，y→0，輸入值yin,xin的限制條件是|atanh (yin/xin)|≤1.1182，可以用來計算方根以及反雙曲正切函數的值.

在旋轉模式下，x→0輸入zin的限制條件是|zin|≤1.1182，可以用來計算雙曲余弦和雙曲正弦函數.

2.6 CORDIC算法小結

當m取不同的值時，可以得到CORDIC的三種不同計算方式，在各個計算方式下，通過多次迭代，可以計算得到多個函數的值，比如三角函數、雙曲函數以及開方運算等.表2描述了線性系統、圓周系統和雙曲系統在旋轉和向量模式下的迭代結果.

表2 CORDIC算法在各種模式下的迭代結果[8]

圖2 圓周系統的旋轉模型迭代結果

〔1〕孔德元.針對正弦余弦計算的CORDIC算法優化及其FPGA實現[D].中南大學碩士論文，2008.1-3.

〔2〕J.E.Volder.The CORDIC trigonometric computing technique [J].IRE Trans.on Electron.Computers,vol. EC-8,1959.330-334.

〔3〕Xiaobo Hu,Ronald G.Harber,and Steven C.Bass, Expanding the Range of Convergence of the CORDIC Algorithm,IEEE Trans.on Computers,[J].vol.40,no.1, 1991.Jan.P.13-P.21.

〔4〕曹劍英.M倍降速遞歸流水線技術實現正切余切函數[J].通信技術，2013(05).

O241

A

1673-260X（2014）04-0021-03