混沌分形的計算機模擬

左常玲，傅廷亮

（安徽三聯學院 信息與通信技術系，安徽 合肥 230601）

混沌分形的計算機模擬

左常玲，傅廷亮

（安徽三聯學院 信息與通信技術系，安徽 合肥 230601）

混沌和分形吸引子的研究是較為復雜的，在計算機出現以前觀察混沌吸引子的動態演化幾乎不可能.這類吸引子以其特殊形狀及內在復雜性而成為分形領域的一大難題，但借助計算機的可視化軟件，人們可以交互地觀察吸引子的演化，對吸引子的研究起到了極大作用.本文從數學原理及計算機實現兩個角度研究了由微分方程產生的混沌分形，提出了合理的圖形繪制算法，使用OpenGL編制出交互程序，并以Lorentz吸引子和Ueda吸引子為例分別繪出其三維演化圖形.

混沌；分形；程序設計；吸引子；微分方程

1 引言

分形理論是當今世界十分風靡和活躍的新學科，其概念是美籍法國數學家曼德布羅德（B.B. Mandelbort）首先提出的.分形一詞英文為Fractal，是由拉丁語Frangere一詞創造而成，該詞本身具有“破碎”和“不規則”兩個含義.分形學科的發展，主要有兩個方面：一方面是科學與自然中的許多現實例子的相似性得到了驗證；另一方面，隨著分形分析新工具的產生，用于研究分形集的數學理論與方法有了巨大的發展，其中大部分源自幾何測度論.

分形理論是非線性科學的前沿和重要分支，作為一種方法論和認識論,其啟示是多方面的:分形整體與局部形態的相似,啟發人們通過認識部分來認識整體,從有限中認識無限；分形揭示了介于整體與部分、有序與無序、復雜與簡單之間的新形態、新秩序；分形幾何的主要價值在于它在極端有序和真正混沌之間提供了一種可能性.分形最顯著的性質是：本來看似十分復雜的事物，事實上大多數均可用僅含很少參數的簡單公式來描述.其實這個簡單并不那么簡單，它蘊含著復雜.分形幾何中的迭代法為我們提供了認識簡單與復雜辯證關系的生動例子[1-4].

2 混沌的定義

人們做了各種努力企圖給分形一個嚴格的數學定義，但是這些定義都很難適用于一般的情形.最常規的描述是，如果一個歐幾里得空間中的集合具有下面所說的全部或大部分性質，它就是分形：

該集合具有精細的結構，即有任意小比例的不規則細節.

該集合是如此的不規則，以至于無論它的局部或整體都不能用微積分或傳統的集合語言來描述.

該集合具有某種統計或近似意義上的自相似或自仿射性質.

該集合的分形維數嚴格大于它的幾何拓撲維數.

分形理論的基礎是分形幾何，而分形幾何中復雜的分支莫過于由微分方程的解逼近的混沌吸引子.分形幾何主要研究吸引子在空間上的結構，它和混沌有共同的數學祖先——動力系統.如果把非線性動力系統看成是一個不穩定的發散過程，那么由迭代法生成分形吸引子正好是一個穩定的收斂過程.有的混沌學家說，混沌是時間上的分形，而分形是時間上的混沌.混沌具有兩個特征：第一個特征是系統狀態對初始條件的靈敏依賴性，即初始條件的微小差別會隨時間的演化呈指數增長.換言之，如果初始條件只有有限的精度，則隨時間的增長，其狀態的精度將變得越來越差，最終不可接受和長期不可預測；混沌的第二個特征是其吸引子具有奇異吸引子結構.奇異吸引子又叫隨機吸引子，它位于空間中，具有分數維，其軌線形狀極其復雜，并具有結構穩定性.隨著時間的演化，其軌線是不重疊的.奇異吸引子最典型的特征是其具有無窮嵌套的自相似結構，即取出吸引子中的一小部分進行放大，它具有與原吸引子相同的內部結構，在將放大后的吸引子取出一小部分再放大，它仍然具有與原吸引子相同的內部結構，如此循環，以至無窮.當系統同時具備這兩個特征時，則認為該系統存在混沌[5，6].

動力系統的奇異吸引子通常都是分形集，它們產生于非線性函數的迭代和非線性微分方程中. 1963年，氣象學家洛倫茲（E.N.Lorentz）在研究流體的對流運動時，發現了以他的名字命名的第一個奇異吸引子，它是一個典型的分形集.1976年，法國天文學家伊儂（M.Henon）考慮標準二次映射迭代系統時獲得伊儂吸引子，它具有某種自相似性和分形性質.1986年勞威爾（H.A.Lauwerier）將斯梅爾的馬蹄映射變形成勞威爾映射，其迭代下不穩定流形的極限集成為典型的奇異吸引子，它與水平線的截面為康托集.其后又有諸多的新發現.動力系統中另一類分形集來源于復平面上解析映射的迭代.朱利亞（G.Julia）和法圖（P.Fatou）于1918-1919年間開創這一研究.他們發現，解析映射的迭代把復平面劃分成兩部分，一部分為法圖集，另一部分為朱利亞集（J集）.他們在處理這一問題時還沒有計算機，完全依賴于他們自身固有的想象力，因此他們的智力成就受到局限.隨后50年間，這方面的研究沒有得到什么進展.隨著可用機算機來做實驗，這一研究課題才又獲得生機.1980年，曼德爾布羅特用計算機繪出用他名字命名的曼德爾布羅特集（M集）的第一張圖來.其后道迪（A.Douady）構造了含參二次復映射fc，其朱利亞集J（fc）隨參數C的變化呈現各種各樣的分形圖象，茹厄勒（D.Ruelle），茄勒特（L.Garnett）等人都在這一領域取得很好的成果，由于篇幅所限，在此不一一列出.

3 關于OpenGL

在使用迭代方程組方法模擬混沌吸引子過程中存在誤差，只能繪制出方程解得近似圖形，且由于計算機時間及空間的限制，要想展現一個吸引子的全貌幾乎是不可能的.可行的方法是：提供一個交互的環境，允許用戶在空間內以任意的角度進行觀察，并且可以指定迭代運算的精度，顯示吸引子的演變軌跡圖形.

在可視化交互式程序設計環境中,OpenGL是個很好的解決方案，它的兼容性好，能在不同的平臺下運行.OpenGL實際上是一種圖形與硬件的接口.它包括了120個圖形函數,開發者可以用這些函數來建立三維模型和進行三維實時交互.與其它圖形程序設計接口不同,OpenGL提供了十分清晰明了的圖形函數，因此初學者也能利用OpenGL的圖形處理能力和1670萬種色彩的調色板設計出三維圖形以及三維交互軟件.OpenGL強有力的圖形函數不要求開發者把三維物體模型的數據寫成固定的數據格式，允許開發者利用其它不同格式的數據源.這種靈活性極大地節省了開發者的時間,提高了軟件開發速度.OpenGL正是提供了這種直觀的編程環境和一系列函數，大大地簡化了三維圖形程序.

在用OpenGL編制圖形程序時要建立圖形和數字之間的聯系，為了使被顯示的物體數字化，要在被顯示的物體所在的空間中定義一個坐標系.這個坐標系的長度單位和坐標軸的方向要適合對被顯示物體的描述，這個坐標系稱為世界坐標系.計算機對數字化的顯示物體使用二維直角坐標系，這個坐標系稱為屏幕坐標系.

投影變換是一種很關鍵的圖形變換，OpenGL中只提供了兩種投影方式，一種是正射投影，另一種是透視投影.圖1所示的是正射投影，圖2所示的是透視投影.

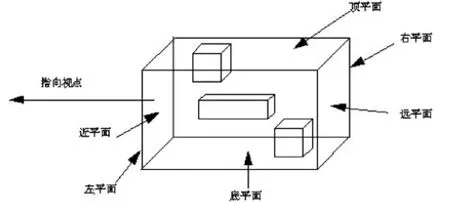
圖1 正射投影示意圖

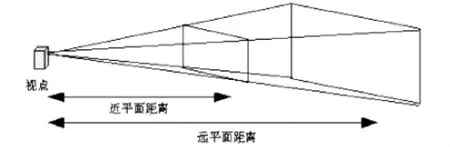
圖2 透視投影示意圖

4 分形圖形的算法和計算機實現

至今人們已發現眾多的奇異吸引子，本文只對Lorentz吸引子和Ueda吸引子進行模擬，從各個不同的角度得到了許多演變圖形.Lorentz吸引子和Ueda吸引子都是典型的分形集，法國天文學家伊儂考慮標準二次映射迭代系統時獲得伊儂吸引子也具有某種自相似性和分形性質.在研究非線性方程演化過程時，迭代法是可用的工具.我們可以用一組變量來描述一個物理系統的狀態，這些變量都是時間t的函數，在所研究的系統中還存在某些可以調節的“控制參量”，它們可能影響系統的運行狀態.最簡單的情景是固定一組參量，把時間變量離散成一系列的等間隔的時間步長△t，計算各時間段的系統狀態如何變化.在只有一個狀態變量x時，這個演化過程可以由一個非線性函數描述.對系統方程進行多次迭代求解，得到一系列的結果數據，繪出系統時間演變的變化圖形（見后面圖3，圖4，圖5和圖6），從圖上看，結果圖形看起來顯得模糊“混沌”，通常人們稱其為周期性的混沌帶.混沌帶并非亂成一片，從混沌帶中不少透明處清楚地看到存在著多點周期.考察每個窗口開始的邊界附近的情況就會發現，雖然運動軌道總體上是混亂的，但迭代的絕大多數點集中在周期軌道開始發生的點附近.如圖3那樣把迭代的值和迭代次數（即時間）畫出圖形，則清楚地看到圖中出現一陣混沌，一陣規則的所謂陣發（間歇）現象.研究發現，以上迭代具有極大的普遍性，很多其它的非線性系統產生混沌的過程、混沌中的窗口情形、自相似結構等等都與一維迭代類似，因為它可以反映出復雜性現象中的內在規律性.

結合本文的需求與OpenGL的特性，我們采用了更加通用的方式去編寫程序：先實現一個通用的3D引擎，然后在上面進一步開發出專用的分形庫.

其基礎數據結構接口如下（由于程序代碼太多，此處只列出很少的實例）：

該數據結構的好處在于，不使用額外空間，與傳統的C語言數組完全兼容，且向上兼容boost庫和STL.在性能方面，通常操作都與傳統的C語言數組性能相當，在矩陣乘法等算法上沒有特殊優化，使用接口設計簡單明了.此外，使用傳統數組的程序可以十分方便的轉由vector代理，幾乎不用付出什么代價，還能得到良好的兼容性.

5 程序運行的結果

本文用程序對Lorenz吸引子和Ueda吸引子進行模擬后給出以下的圖形顯示，操作者可方便的通過指點設備與程序參數進行不同視點的觀察和互動，動態地調整參數，顯示多幅三維演變圖形.圖3、圖4是Lorenz吸引子的圖象，Lorenz吸引子由以下方程給出：

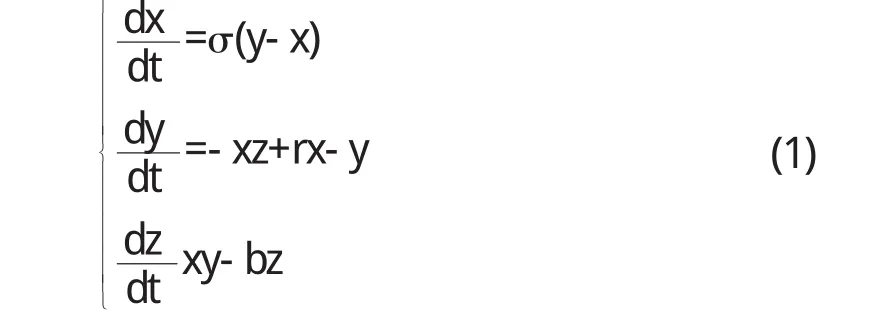
其中σ,r,b是正的參數，這是一個自治的三階方程.當參數不同時，方程的狀態就不同.

圖3 Lorentz attractor在混沌態的三滅點透視圖像

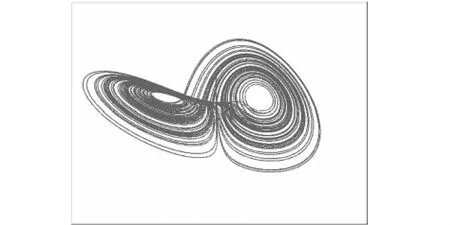
圖4 Lorentz attractor在混沌態的三滅點透視圖像Z-axis

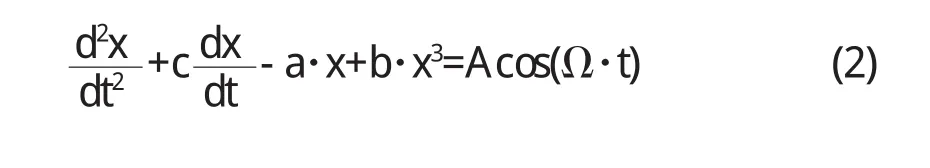
該方程可化為：

其中，

(a=1,b=1,c=1.5,A=0.3)

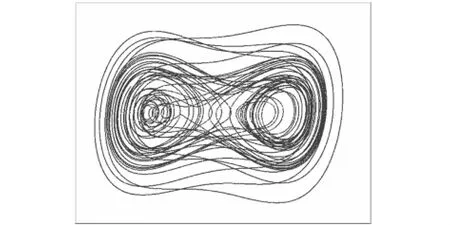
圖5 Ueda attractor在混沌態的三滅點透視圖像

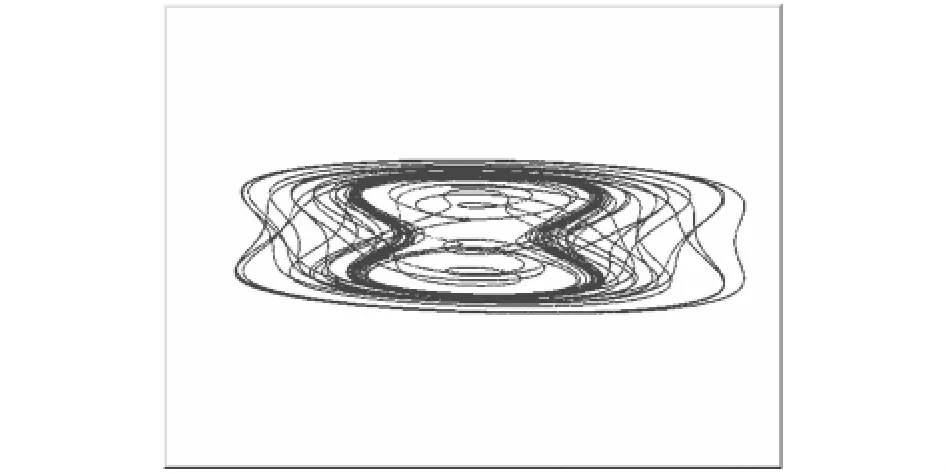
圖6 Ueda attractor在臨界態的三滅點透視圖像

6 結束語

混沌分形吸引子的細節是無窮無盡的，而人們可以通過有限的部分去認識這些無限的整體，分形本身帶來的影響是不可估量的，但更重要的是，通過對它的研究，導致了許多新思想、新工具的誕生，本文正是在有限的計算機環境下去模擬復雜的分形，希望在分形的研究領域起到拋磚引玉的作用.

〔1〕劉華杰.分形藝術[M].湖南：湖南科學技術出版社，1998.18-96.

〔2〕KJ Falconer.Techniques in Fractal Geometry [M].ISBN 7-81054-393-8,July 1997.58-112.

〔3〕BB Mandelbrot,DE Passoja,AJPaullay.Fractal Character of Fracture Surfaces of Metals[J]. Nature,1984，308(19):721-722.

〔4〕JM Sm ith.Fundamentals of Fractals of Engineers and Scientists[M].John W iley&Sons,1991: 125-208.

〔5〕齊東旭.分形及其計算機生成[M].北京：科學出版社，1994.25-102.

〔6〕鐘云霄.混沌與分形淺談[M].北京：北京大學出版社，2010.20-65.

TP391.41

A

1673-260X（2014）04-0027-04

安徽三聯學院質量工程教學研究基金項目（NO.12zlgc011）;安徽省高等教育振興計劃新專業建設項目（2013zypz082)