城鎮化與經濟增長依從關系的實證研究

石瓊強

（安徽財經大學 數量經濟研究所，安徽 蚌埠 233030）

城鎮化與經濟增長依從關系的實證研究

石瓊強

（安徽財經大學 數量經濟研究所，安徽 蚌埠 233030）

本文選取我國城鎮化率與人均實際GDP兩個指標分別作為我國城鎮化水平和經濟增長水平的指標，并根據1978～2011年我國城鎮化率與人均實際GDP的時間序列數據，利用ADF單位根檢驗、E-G協整檢驗、Granger因果檢驗、VEC模型，對我國城鎮化與經濟增長依從關系進行動態計量分析.主要結論有：城鎮化水平與經濟增長水平之間從長期來看存在均衡關系；二者之間存在單向的城鎮化水平→經濟增長的因果關系；城鎮化水平→經濟增長水平呈現出同方向變化，即城鎮化水平、經濟增長水平同增或同減.從一段較長時間來看，城鎮化率增加1%，將推動人均實際GDP上升2.97%，而經濟增長對于城鎮化并無明顯影響；本期人均實際GDP的變動主要受其前一期變動、城鎮化率的前一期變動和前一期偏離均衡狀態的程度的影響，且對于前一期偏離的調整速度為0.06，而本期城鎮化率的變動主要受到其前兩期的變動和其前一期偏離均衡狀態的程度的影響，且對于前一期偏離的調整速度為0.06.

ADF單位根檢驗；E-G協整檢驗；Granger因果檢驗；VEC模型

1 引言

李克強總理曾經指出：“我國已進入中等收入國家行列，未來幾十年我國經濟發展的最大潛力在城鎮化……”.可見，中央領導對于城鎮化水平的提高在促進我國經濟增長的作用方面還是給予充分肯定的.1978年，我國的城鎮化率僅為17.92%，與2011年的51.27%相比平均每年增長約0.98%；同時我國人均實際GDP（1980年價）從1978年的409元增長到2011年的6576元.城鎮化水平的快速上升對于經濟的迅猛增長發揮了很重要的作用，且已經逐漸成為經濟發展的重要引擎.對于城鎮化水平與經濟增長水平關系國外學者進行了大量的研究.最早對城鎮化水平與經濟增長水平關系進行研究的是美國著名的經濟學家Lampard，他研究認為城市的發展速度與城市所處的城鎮化階段高度一致. Luisit Bertinelli&Ericstrob[1]通過構建二者的半參數模型認為城鎮化水平與經濟增長水平之間并無系統聯系，而這與Lampard的研究結果截然相反.國內關于二者關系的研究成果也很豐富.傅鴻源、鐘小偉、洪志偉[4]利用美國、英國和加拿大不同時間的數據通過計量分析認為隨著城鎮化水平的提高，美國、英國與加拿大的人均GDP都增加，而且隨著人均GDP的增長，各國的城鎮化水平都上升.李秀敏、趙曉旭、朱艷艷[6]利用我國28個省22年的數據，通過構建面板計量模型，分析發現：高城鎮化水平能促進經濟增長水平的提高，但是隨著不同省所處的經濟發展水平的提高，城鎮化水平的提高對于經濟增長水平的促進作用逐漸削弱.可見國內外學者對與城鎮化水平與經濟增長水平關系的研究結論不盡相同.總的來說，對于城鎮化水平與經濟增長水平關系的研究，定性分析較多，相比而言定量分析則較少；同時由于數據選取的不同、考慮問題的角度與采用的方法不同，結論也不盡相同.因此本文換一個角度，通過構建VEC模型對城鎮化水平與經濟增長水平的長期與短期波動影響因素進行定量分析.

2 數據及處理

本文選取我國城鎮化率與人均實際GDP兩個指標分別作為我國城鎮化水平和經濟增長水平的指標，并根據1978～2011年我國城鎮化率與人均實際GDP的時間序列數據進行分析.其中，城鎮化率=我國城鎮總人口/我國總人口（年末），記為k；根據按1980年價格計算的1980年不變價GDP與按不變價格計算的GDP指數計算可得到按1980不變價調整的實際GDP，在實際GDP的基礎上在除以我國總人口（年末）即可得到我國的人均實際GDP，即為g.本文采用的我國城鎮總人口、我國總人口（年末）、1980年不變價GDP、GDP指數的數據均來自2012年《中國統計年鑒》.為了減小數據波動、避免“偽回歸”和防止模型中可能存在異方差性，對城鎮化率序列和人均實際GDP序列分別進行自然對數變換，得到自然對數后的序列，分別記為lnk，lng.

3 實證分析

3.1 單位根檢驗

本文利用ADF單位根檢驗法對序列lng、lnk進行平穩性檢驗.

進行ADF單位根檢驗關鍵在于確定單位根檢驗回歸方程的形式，通過繪制lnk序列和lng的時間趨勢圖可知：lng序列和lnk序列的均值均不為零，并且呈現明顯的趨勢.因此選擇包含截距項和時間趨勢項的形式進行檢驗.檢驗方程滯后階數的選擇以SIC最小為準則.lnk、lng序列的ADF檢驗結果（見表1）表明：它們的檢驗t統計量都大于10%的顯著性水平下的臨界值，因此序列lnk和lng在10%的顯著性水平下都至少包含一個單位根，即為非平穩序列.

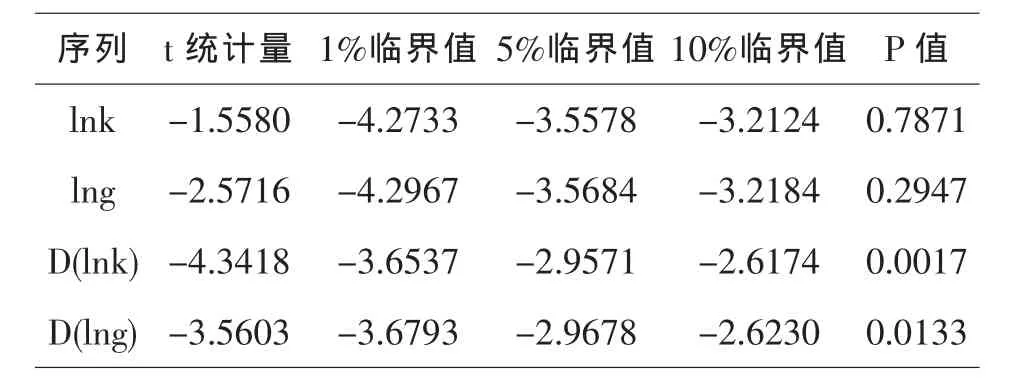
表1 原序列和差分序列的ADF單位根檢驗結果

將lnk和lng序列做一階差分，得到D(lnk)和D(lng)序列，檢驗方程形式與滯后階數的確定與前面相同.D(lnk)和D (lng)序列的ADF檢驗結果（見表1）表明：它們的檢驗t統計量小于1%顯著性水平下的臨界值，因此D(lnk)和D(lng)序列在1%的顯著性水平下不存在單位根，即為平穩序列.綜上所述，lnk和lng序列都是I(1)序列.

3.2 協整檢驗

對于檢驗兩個變量間的協整關系，一般采用Engle-Granger兩步檢驗法，簡稱E-G兩步法.因為lnk和lng都是一階即同階單整序列，所以可以進一步檢驗二者的協整性.

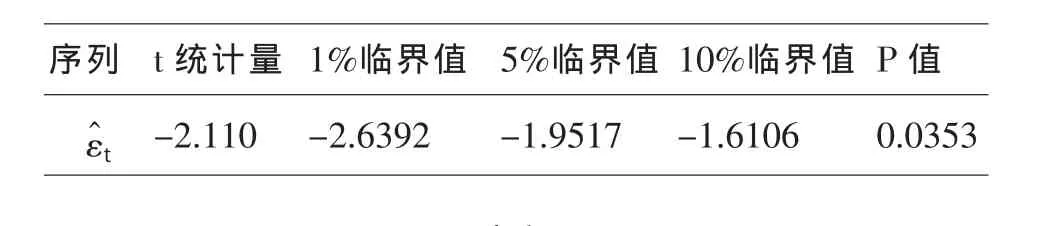
表2 殘差序列的ADF單位根檢驗結果

模型估計得到：

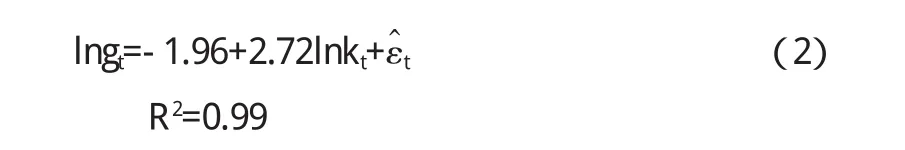
同樣，檢驗方程滯后階數（p=1）由SIC最小為準則，且檢驗方程不包含常數項和時間趨勢項，結果（見表2）顯示：其t統計量小于5%顯著性水平下的臨界值，即在5%的顯著性水平下序列不存在單位根，即平穩序列，因此～I(0).因而根據協整的定義，序列lnk和序列lng之間具有協整關系，即為CI(1,1)的，協整向量為（1，-2.72）.

3.3 Granger因果檢驗

Granger曾指出：若兩個變量之間存在協整關系，那么這兩個變量一定存在單向或者雙向Granger因果關系.由于序列lnk和lng之間存在協整關系，那么序列lnk和lng之間一定存在某種形式的Granger因果關系.進行Granger因果檢驗關鍵在于確定其檢驗式的滯后階數，而其檢驗式與

第一步：利用OLS估計方程：對應VAR模型方程是相同的，因此首先需要確定其對應VAR模型的最佳滯后階數，然后取與VAR模型最佳滯后階數相同的階數進行Granger因果檢驗.

建立VAR(p)模型：

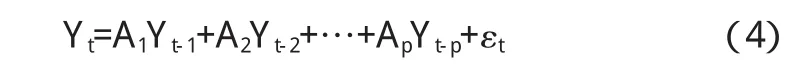
其中Yt=(lng,lnk)'.一般確定最優滯后階數的準則有AIC和SIC取值最小，Eviews6軟件可自動實現，進而確定p=3,即Granger因果關系檢驗的檢驗方程的滯后長度為3.檢驗結果（見表3）顯示：lnk在10%的顯著性水平下是lng變化的Granger原因，相反相同顯著性水平下lng則不是lnk變化的Granger原因.

表3 Granger因果檢驗結果

因此，根據以上分析，序列lng和lnk之間存在從lnk到lng的單向因果關系，即lnk lng，而不存在相反方向的因果關系.

3.4 向量誤差修正模型

由于序列lng和lnk是存在協整關系的變量序列，因此可以建立VEC模型.

VAR(p)可以寫成方程（5）的形式，其中ΔYt=(Δlngt，Δlnkt)'，ECMt-1為誤差修正項，它反映了序列lng和lnk之間的協整關系，即Yt-1偏離均衡關系狀態的程度，而其系數向量α則表示本期對上一期偏離均衡的調整速度.ΔYt-i表示Yt滯后差分項，Γi表示ΔYt對本期Yt的變動對于前i期Yt的變動（即ΔYt-i，）的反應程度.

根據VAR模型估計結果顯示最優滯后階數為3，根據方程（5）可知對于VEC模型滯后區間應設定為2.模型估計結果為：

其中，VECMt-1=lngt-1-2.791lnkt-1+2.217為VAR(3)的誤差修正項，反應了序列lng與序列lnk之間的長期均衡關系.模型的AIC準則和SC準則分別為-11.4665和-10.8189，都比較小.

利用上述所估計的模型我們可以對lng和lnk的短期變動分別進行分析.實際上方程（6）包含兩個方程，分別為方程（7）和方程（8）.

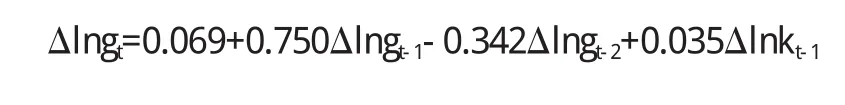
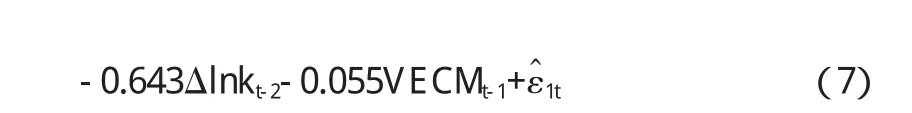
根據方程（7）可以看出對于lng的短期變動，應該分為兩個部分：一部分是由于前兩期lng的變動（即lngt-1和lngt-2）和前兩期lnk的變動（lnkt-1和lnkt-2）的影響，另外一部分是由于上期lng偏離長期均衡關系（即VECMt-1）的影響.當上一期lng變動lngt-1和上二期lng變動lngt-2分別增加1，當期lng變動lngt將分別表現為增加0.75和減少0.34，當lnkt-1和lnkt-2分別增加1，當期lng變動講分別表現為增加0.04和減少0.63.若前一期人均GDP（即lng）沒有偏離長期均衡關系，則VECMt-1，那么當期lng的變動全部來自于第一部分；若前一期lng偏離了長期均衡關系，則VECMt-1≠0，則為了維持lng與lnk的長期均衡關系，當期將以-0.06的速度對前一期lng與lnk的非均衡關系做出調整，將其拉回到長期均衡狀態.

同理，根據方程（8）可以看出對于lnk的短期變動也可以分為兩部分：一為前兩期lnk的變動(即Δlnkt-1和Δlnkt-2)、前兩期lng的變動（即Δlngt-1和Δlngt-2）的影響，二為上期lnk偏離長期均衡關系（即VECMt-1）的影響.當上一期lnk變動Δlnkt-1和上二期Δlnkt-2分別增加1，當期lnk變動將分別增加0.33和0.39，當上一期lng變動Δlngt-1和上二期lng變動Δlngt-2分別增加1，當期lng變動Δlngt將分別減少0.06和減少0.03.當前一期lnk偏離了lng與lnk的長期均衡關系，當期將以0.06的速度對前一期lnk與lng的非均衡關系做出調整而使其回到均衡狀態.

4 結論

通過選取1978-2011年我國城鎮化率與人均實際GDP的相關數據，并構建VEC模型對城鎮化率與人均實際GDP的依從關系進行動態計量分析.結果表明：

（1）從長期來看，城鎮化與經濟增長之間存在均衡關系，且這種均衡關系是穩定的.二者之間存在單向的城鎮化水平→經濟增長的因果關系；城鎮化水平→經濟增長水平呈現出同方向變化，即城鎮化水平、經濟增長水平同增或同減.從一段較長時間來看，城鎮化率增加1%，將推動人均實際GDP上升2.97%，而經濟增長對于城鎮化并無明顯影響；

（2）從短期來看，當期人均GDP的變動受到前兩期人均GDP的變動、前兩期城鎮化率的變動、上一期人均GDP偏離長期均衡狀態的程度的影響.而且前一期人均GDP的變動和前1期城鎮化率的變動對于當期人均GDP的變動的作用較大.當期城鎮化率的變動同樣受到前兩期人均GDP的變動、前兩期城鎮化率的變動和上一期城鎮化率偏離長期均衡關系狀態的程度的影響，而前兩期城鎮化率的變動對于當期城鎮化率的變動作用較大，而前兩期人均GDP的變動對于當期城鎮化率的變動的作用很小.

〔1〕LUISIT BERTINELLI,ERIC STROBL.U rban Concentration and Economic Grow th in Developing Countries[J].U rbanization.W orking Paper,CREDIT.2003.3:145-153.

〔2〕HENDERSON J.U rbanization and Econometric Development[J].Annals of Econom ics and Finance.2003.274-342.

〔3〕DAVIS,JAMES C,HENDERSON J.Vemon Evidence on the Political Economy of the U rbanization Process[J]. Journal of U rban Econom ics,Elsevier.2003.98-124.

〔4〕傅鴻源,鐘小偉,洪志偉.城市化水平與經濟增長的中外對比研究[J].重慶建筑大學學報(社科報),2000(3):19-24.

〔5〕李雪松,張瑩,陳關炎.中國經濟增長動力的需求分析[J].數量經濟技術經濟研究,2005(11):27-33.

〔6〕李秀敏,趙曉旭,朱艷艷.中國東、中、西部地區城鎮化對經濟增長貢獻的比較研究[C].中國西部地區城鄉協調發展與社會創新國際學術研討會論文集,2006(10):27-33.

〔7〕宋元梁,肖衛東.中國城鎮化發展與農民收入增長關系的動態計量經濟分析[J]數量經濟技術經濟研究,2005(09): 30-39.

〔8〕楊慧.北京城市化與經濟增長研究[J].經濟與管理,2005 (4):20-24.

〔9〕沈凌,田國強.貧富差別、城市化與經濟增長—一個基于需求因素的經濟學分析[J].經濟研究,2009(1):17-29.

〔10〕楊開忠.中國城市化驅動經濟增長的機制與概念模型[J].城市問題,2001(3):4-7.

〔11〕段瑞君,安虎森.中國城市化和經濟增長關系的計量分析[J]經濟問題探索，2009(3):26-30.

〔12〕李金昌,程開明.中國城市化與經濟增長的動態計量分析[J].財經研究，2006（9）:19-30.

〔13〕王小魯.城市化與經濟增長[J].經濟社會體制比較,2002 (1):23-32.

〔14〕樊歡歡,李嫣怡,陳勝可.EVIEWS統計分析與應用[M]. 2011.199-282.

〔15〕高鐵梅.計量經濟分析方法與建模-Eviews應用及實例[M].2009.267-299.

F224.0

A

1673-260X（2014）04-0099-03