基于Weibull分布的高速自潤滑關節軸承可靠性分析
李彥偉,林晶,張令,趙穎春
(中國航空綜合技術研究所,北京 100028)
高速自潤滑關節軸承主要由內圈、外圈和自潤滑襯墊3部分組成[1],是一種可以實現高頻擺動的自潤滑關節軸承。自潤滑關節軸承靠內圈與外圈內球面粘貼的自潤滑襯墊的接觸面滑動,所以磨損量是判定軸承壽命的主要依據。
由于高速自潤滑關節軸承壽命服從Weibull分布,故可采用Weibull分布模型進行可靠性分析。Weibull分布模型參數的精度是軸承可靠性分析的關鍵,目前常用的參數估計法[2]中圖估計法簡單方便,但人為因素影響較大,所估計的參數精度較差;極大似然估計法獲得的參數精度較高,但計算復雜繁瑣;最佳線性無偏估計和最佳線性不變估計等方法都需借助專用表格,使用方便,但表格數量很大,且無表格之處無法使用;而最小二乘估計法能實現分布函數的線性化,是Weibull分布模型參數估計的一種較好方法。
試驗數據是軸承可靠性分析的基礎,但在試驗過程中,經常出現試驗磨損量未達到額定磨損量而試驗中止的情況,產生了不完全試驗數據。平均秩次法根據試驗完成產生的完全試驗數據和試驗中止產生的不完全試驗數據估計所有可能的秩次,求出平均秩次,代入近似中位秩公式,得到經驗分布函數,充分利用試驗數據的同時也取得了更加精確的參數估計值。下文采用結合平均秩次法的最小二乘參數估計法對高速自潤滑關節軸承進行可靠性分析。
1 Weibull分布模型
Weibull分布模型[3]是近年來在軸承可靠性分析中使用最廣泛的模型之一,Weibull分布的分布函數為
(1)
分布密度函數為
(2)
可靠度函數為
(3)
失效率函數為
(4)
式中:t為時間;η為尺度參數;β為形狀參數。
2 參數估計
2.1 最小二乘參數估計
最小二乘估計是對線性函數中的未知參數進行估計,是Weibull分布模型參數估計的一種較好方法[4]。
將(1)式變形,得
(5)
兩邊取自然對數,得
lnln[1/(1-F(t))]=β(lnt-lnη)。
(6)
令
x=lnt,
(7)
y=lnln[1/(1-F(t))],
(8)
A=β,
(9)
B=-βlnη,
(10)
則(6)式可轉化為
y=Ax+B。
(11)
對于線性回歸方程(11)式,回歸系數A,B的最小二乘估計解為
(12)
(13)
在Weibull分布模型參數的最小二乘估計中,提高經驗分布函數的精度即可求出一條偏差最小的回歸直線和最符合實際的回歸系數估計值。
2.2 平均秩次法
已有的經驗分布函數計算方法是通過近似中位秩公式或直接查中位秩表[5]得到,誤差較大。近似中位秩公式為
(14)
式中:i為完成試驗的試件順序號;n為試件數量;ti為第i個試件的試驗時間。
平均秩次法是提高經驗分布函數精度的一種有效方法,其原理是:根據完全試驗數據和不完全試驗數據估計出所有可能的秩次,再求出平均秩次,將平均秩次代入近似中位秩公式,求出其經驗分布函數[6]。
文獻[7]通過實踐總結給出的計算平均秩的增量公式為
(15)
Ai=Ai-1+ΔAi,
(16)
式中:k為所有試件的排列順序號,按試驗完成時間和試驗中止時間的大小排列;Ai為完成試驗的試件的平均秩次;Ai-1為前一個完成試驗試件的平均秩次。
將平均秩次Ai代入(14)式,得
(17)
將試驗完成時間和通過計算得到的經驗分布函數,利用最小二乘參數估計法,擬合出Weibull分布模型的回歸直線,從而確定Weibull分布模型的尺度參數和形狀參數。
3 可靠性分析
為了進行軸承可靠性分析,選擇20套高速自潤滑關節軸承進行磨損壽命試驗。試驗方法主要參照SAE(美國機動車工程師學會)標準AS 81819A,試驗軸承在5.4 kN的徑向載荷下進行高速擺動,擺動角度為±6°,擺動頻率為20.78 Hz,當試驗軸承的磨損量達到0.038 mm時,即可結束試驗[8]。
通過記錄20套軸承達到額定磨損量的時間和試驗中止的時間,并按試驗時間進行排序,結果見表1。表中包含了高速自潤滑關節軸承磨損壽命試驗的完全試驗數據(C)和不完全試驗數據(I),去掉不完全試驗數據,將軸承試驗的完全試驗數據進行排序,建立Weibull分布模型,采用平均秩次法,由(16)、(17)式分別計算平均秩次和經驗分布函數,結果見表2。將計算結果(無量綱)按照最小二乘的原理擬合出最小二乘回歸直線,如圖1所示。
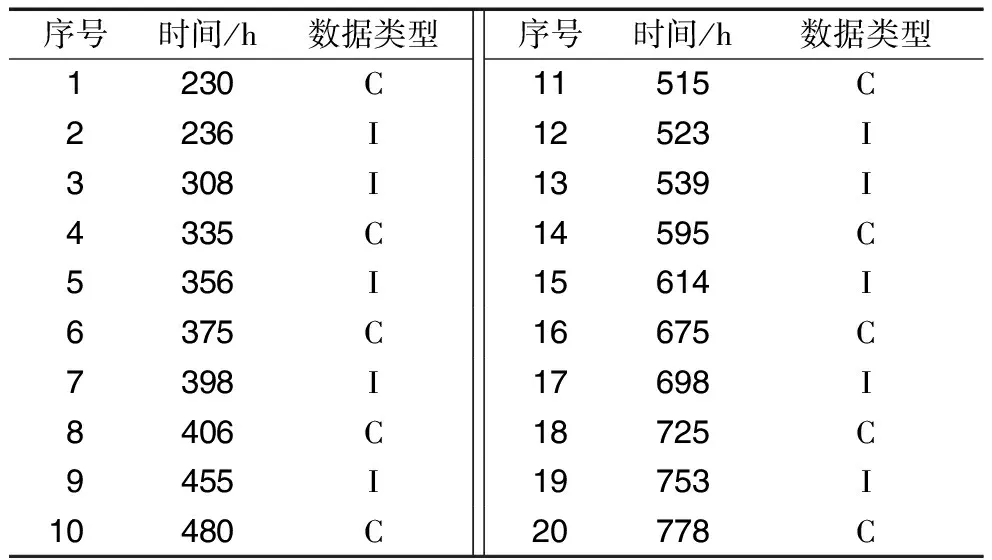
表1 高速自潤滑關節軸承磨損壽命試驗數據
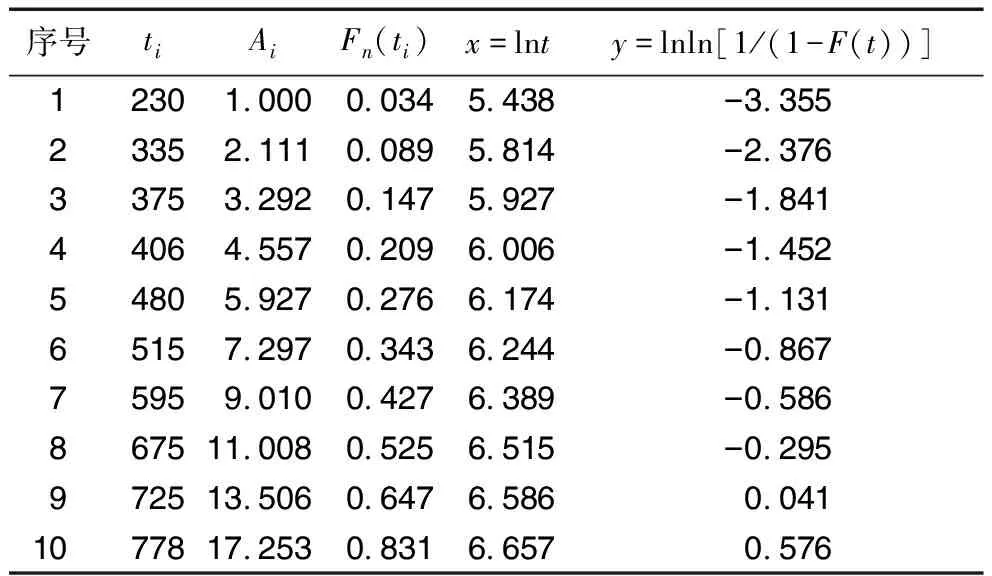
表2 平均秩次法計算的經驗分布函數
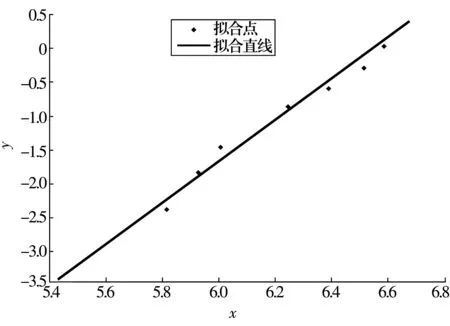
圖1 平均秩次法的最小二乘擬合圖
采用近似中位秩公式,由(10)式計算經驗分布函數,結果見表3。將計算結果(無量綱)按照最小二乘的原理擬合出最小二乘回歸直線,如圖2所示。與圖2相比,圖1中的試驗數據點在擬合直線兩側分布更均勻。S為最小二乘擬合度,其值越趨近于1則擬合越好。采用平均秩次法的計算結果經最小二乘擬合后S=0.985 7,采用近似中位秩公式的計算結果經最小二乘擬合后S=0.974 7,顯然前者更加精確。
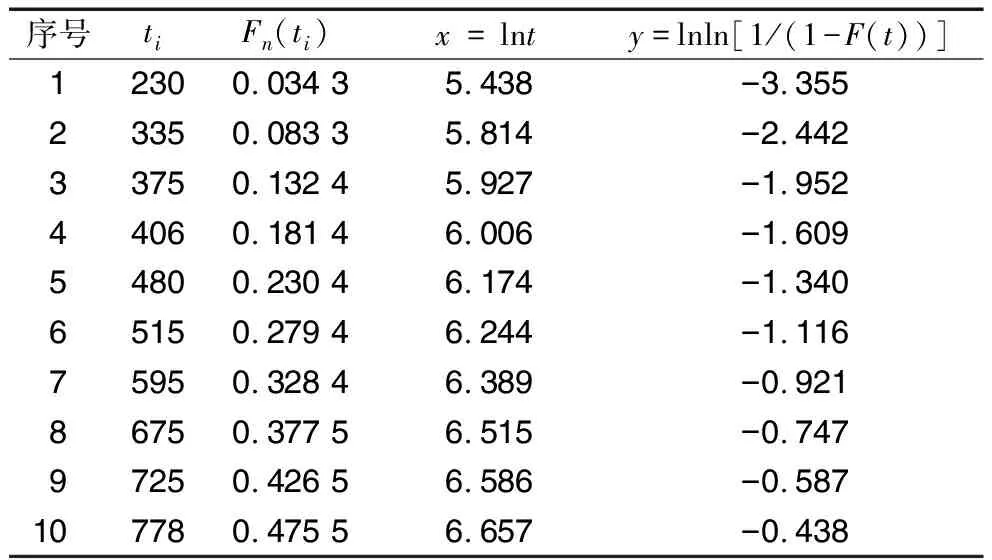
表3 近似中位秩公式計算的經驗分布函數
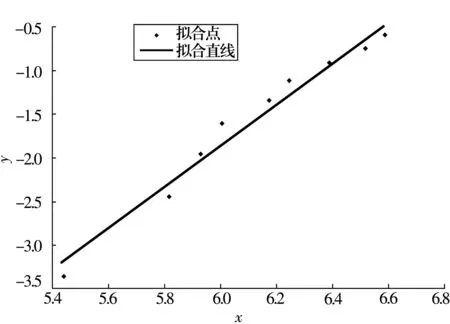
圖2 近似中位秩公式的最小二乘擬合圖
平均秩次法的直線擬合式為
lnln[1/(1-F(t))]=3.037lnt-19.88,
(18)
由(9)、(10)式解得β=3.037,η=696.404。
則分布函數為
(19)
分布密度函數為
(20)
可靠度函數為
(21)
失效率函數為
(22)
當R(t)=0.9時,由(21)式解得可靠度為90%的軸承壽命為t=332 h。
4 結束語
根據完全試驗數據和不完全試驗數據估計出所有可能的秩次,求出平均秩次,代入近似中位秩公式,得到軸承磨損壽命失效分布函數、分布密度函數、可靠度函數和失效率函數;進而計算出可靠度為90%的高速自潤滑關節軸承的壽命。結合平均秩次法的最小二乘參數估計法擬合度高,擬合效果好,并能充分利用試驗數據,得到的參數估計值更加精確。

