諧波小波濾波與HHT在軸承故障診斷中的應用
臧懷剛,王石云,王冀龍
(燕山大學 電氣工程學院 工業計算機控制工程河北省重點實驗室,河北 秦皇島 066004)
滾動軸承在旋轉機械中應用極為廣泛,也是最易損壞的零部件[1],其工作狀態直接影響機械設備的安全與性能。因此,對軸承的狀態監測與早期故障診斷具有重要意義[2-3]。
諧波小波具有良好的盒形頻譜特性,是一個理想的帶通濾波器,可以將任何信號正交、無冗余、無泄漏地分解到相互獨立的頻段上[4]。通過諧波小波將特定頻段的成分與信號的其他頻率成分分解后分離,從而消除了其他頻段成分對該頻段的影響,使一些被淹沒的較弱信號凸顯出來,相當于提高了信噪比。為了研究信號某一特定頻段的成分,對信號的諧波小波分解進行重構時,可將其他頻段的諧波小波系數置為0,只保留該頻段的小波系數。由于諧波小波的正交性,重構的結果只包含該頻段的成分,剔除了其他成分,達到了濾波的目的[5]。
HHT(Hilbert-Huang Transformation)是一種整體變換,雖然不能反映信號的局部信息,但不受Fourier分析的局限,其應用經驗模態分解(Empirical Mode Decomposition,EMD)理論將信號分解成相互獨立的若干固有模態函數(Intrinsic Mode Function,IMF)的和,并對每個IMF進行Hilbert變換,得到信號的瞬時頻率和幅值,能夠精確描繪出信號的時頻譜和幅值譜圖,且具有自適應性,主要用于復雜、非平穩信號的時頻局部分析[6-7]。在此,嘗試將諧波小波濾波去噪與HHT結合,并應用到軸承故障診斷中。
1 算法
1.1 諧波小波原理
諧波小波是一種小波函數。在頻帶[m2π,n2π]內,定義函數的Fourier變換為[8-9]
(1)
時域表達式為
(2)
(2) 式稱為廣義諧波小波[10-11]。當m=1,n=2時為經典諧波小波,諧波小波實部為偶函數,虛部為奇函數。
連續時間信號x(t)的諧波小波變換定義為
(3)
對 (3) 式進行Fourier變換得
(4)
(3)和 (4) 式分別為信號x(t)的諧波小波變換在參數m,n尺度下的時域和頻域表達式,其離散形式可寫為
r=1,2,…,N-1。
(5)
1.2 HHT基本原理
Fourier頻譜的幅值只能反映頻率在信號中實際存在的可能性,而邊際譜的幅值能真實反映頻率在信號中是否存在。利用邊際譜的線性性質進一步給出邊際譜的物理意義,即邊際譜的幅值表示信號在某一頻率各個時刻的幅值之和。每個IMF是滿足以下2個條件的信號:(1)整個信號中零點數與極點數相等或至多相差1;(2)信號上任意一點,由局部極大值點確定的包絡線和由局部極小值點確定的包絡線的均值均為零,即信號關于時間軸局部對稱[12]。
信號x(t)經過EMD處理后可以成為相互獨立的若干IMF分量ci(t)(i=1,2,…,n)和1個殘量rn(t)的線性組合
(6)
對(6)式中的每個本征模函數ci(t)進行Hilbert變換得
(7)
式中:P為柯西主分量。
構造解析信號
(8)
可以求出瞬時頻率為
ωi(t)=dφi(t)/dt。
(9)
則
(10)
式中:Re表示取實部;ai(t),φi(t)為每個固有模態函數ci(t)經Hilbert變換后構造的解析信號的幅值函數和相位函數;此處省略了殘量rn。
Hilbert譜為
(11)
Hilbert邊際譜為
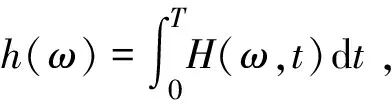
(12)
式中:T為信號總長度。當H(ω,t)或h(ω)中有某一頻率的能量出現時,就表示一定有該頻率的振動波出現,Hilbert邊際譜能比較準確地反映信號的實際頻率成分。
1.3 故障診斷流程
首先,對采集信號進行諧波小波去噪處理,去除噪聲信號對軸承振動信號的干擾;然后,進行EMD處理,得到各個IMF分量;最后,對包含故障頻率的IMF分量進行Hilbert邊際譜分析,診斷出故障類型。故障診斷流程如圖1所示。

圖1 故障診斷流程圖
2 應用分析
2.1 試驗數據分析
以西儲大學的SKF6205-2RS軸承故障數據為例[13],軸承轉速為1 797 r/min,鋼球數為9,鋼球直徑為7.94 mm,球組節圓直徑為39.04 mm,計算得軸承內圈、外圈和滾動體故障特征頻率分別為162,107和141 Hz。對采樣頻率12 kHz、采樣點數2 400的軸承外圈故障信號進行分析,波形如圖2所示。
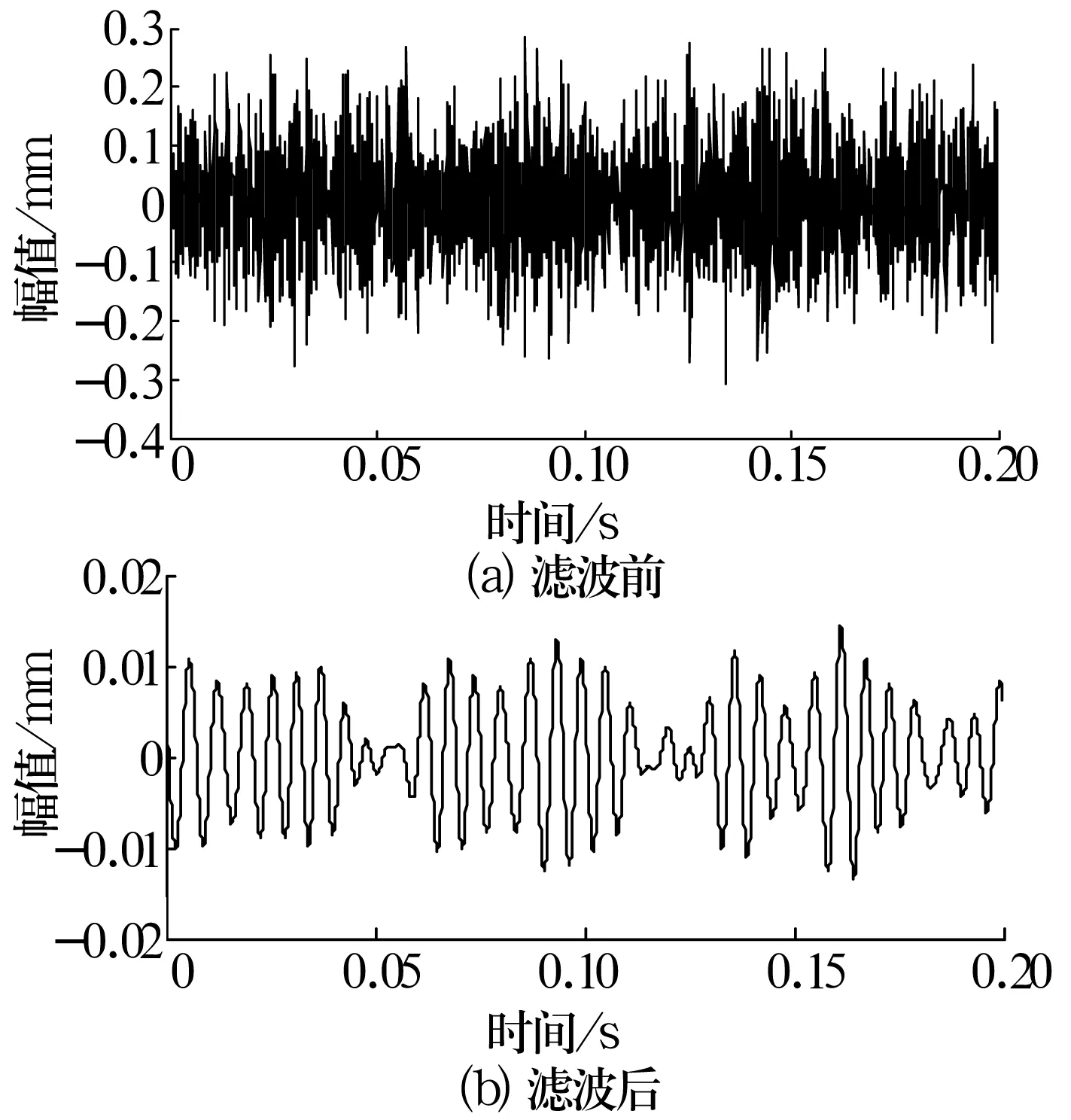
圖2 外圈故障信號的時域波形
由圖2a可以看出,軸承信號淹沒在噪聲中,無法識別故障類型;經過諧波小波濾波處理后,由圖2b可以清楚地看出,諧波小波濾波器可有效消除干擾噪聲,提高信噪比。圖2b中的振動信號呈現有規律的波動,但仍然無法看出信號的故障特征頻率。因此,對信號進行EMD處理,得到不同頻率段的IMF分量如圖3所示。通過分析發現IMF1分量中含有明顯且均勻的沖擊成分,其Hilbert譜如圖4所示。
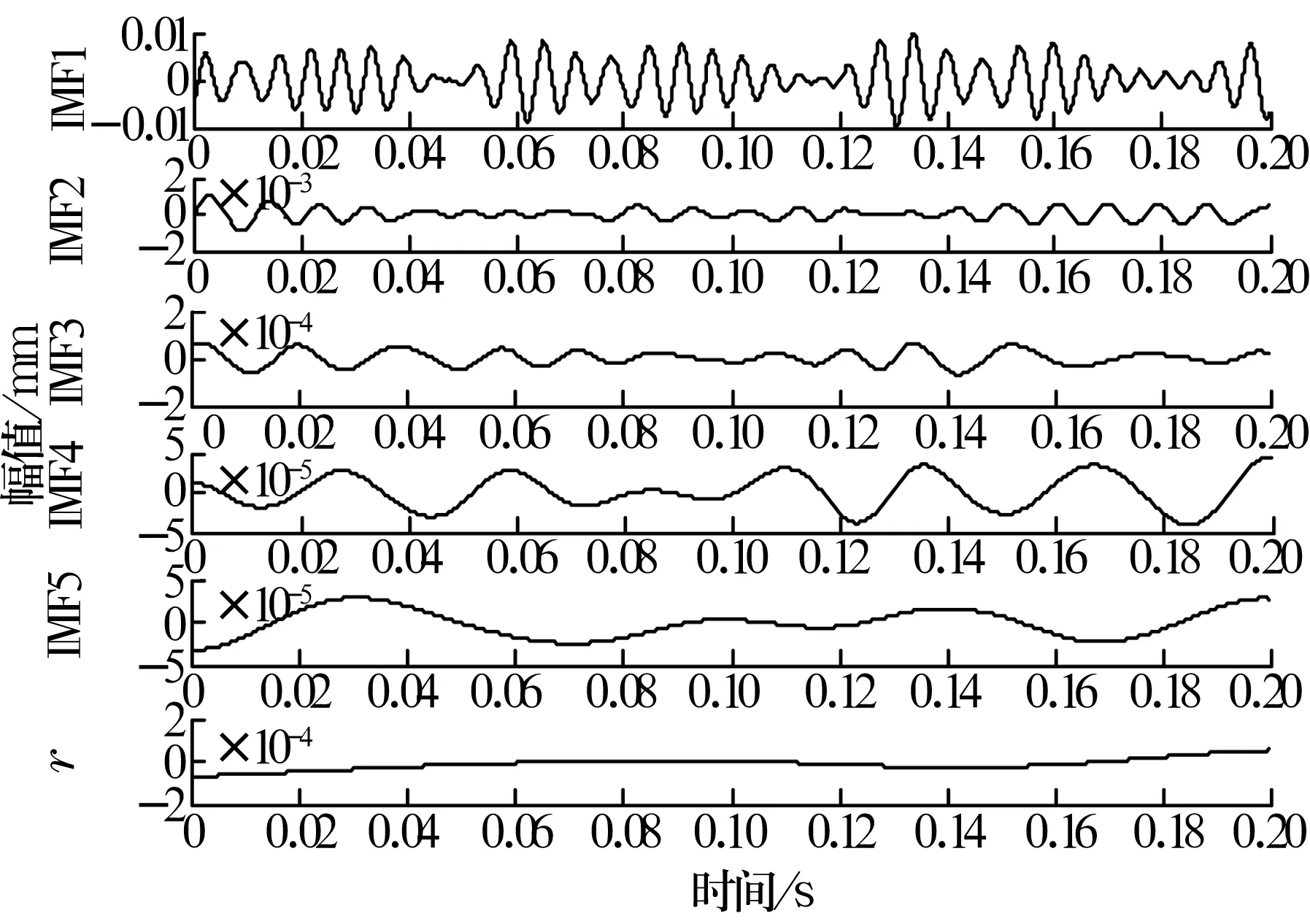
圖3 濾波后經EMD處理的軸承信號
由圖4可以看出,峰譜值為106.3 Hz,與試驗軸承的外圈故障頻率比較接近,可以判斷軸承為外圈故障。
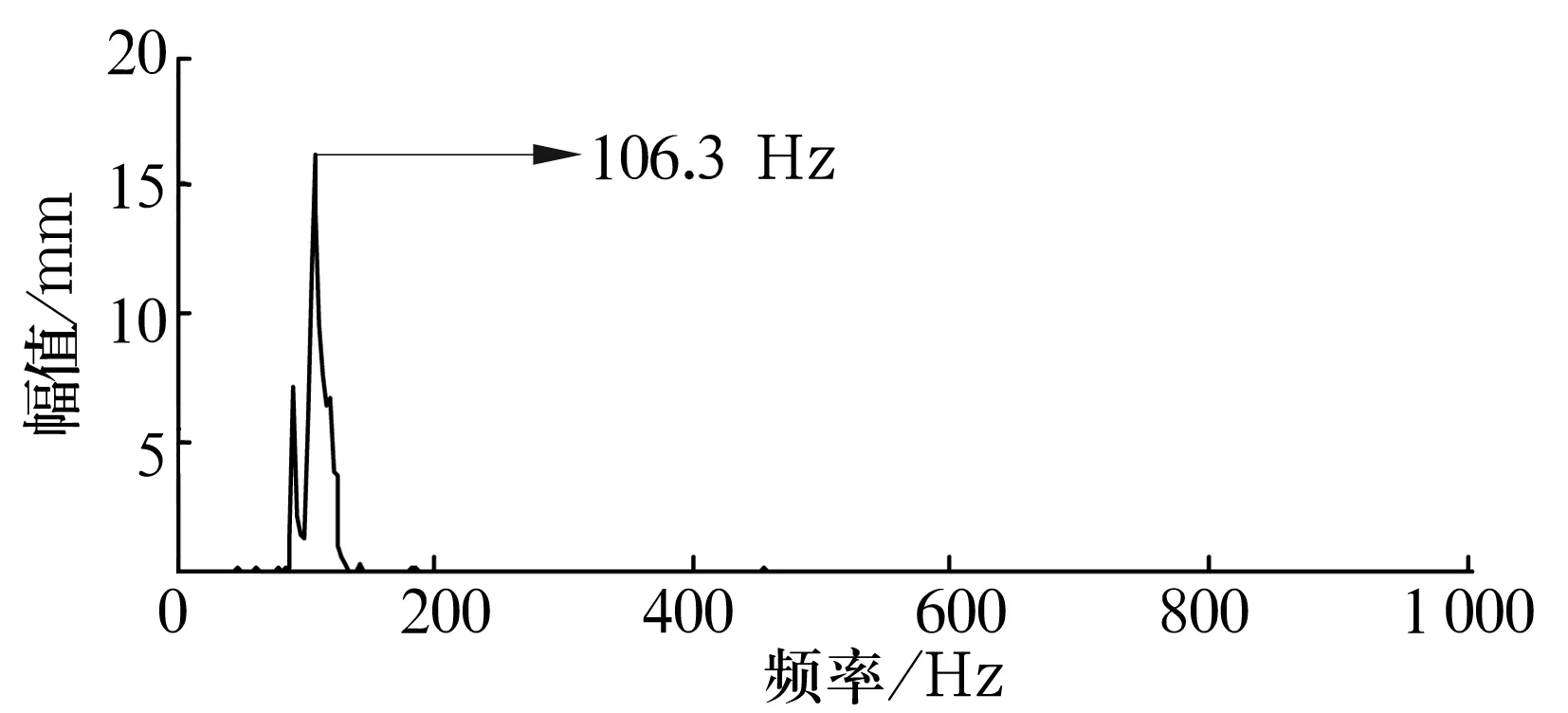
圖4 IMF1的Hilbert邊際譜
若不經諧波小波濾波,直接對信號進行EMD處理,并對包含故障頻率的特征頻率分量進行Hilbert譜分析,結果如圖5所示。
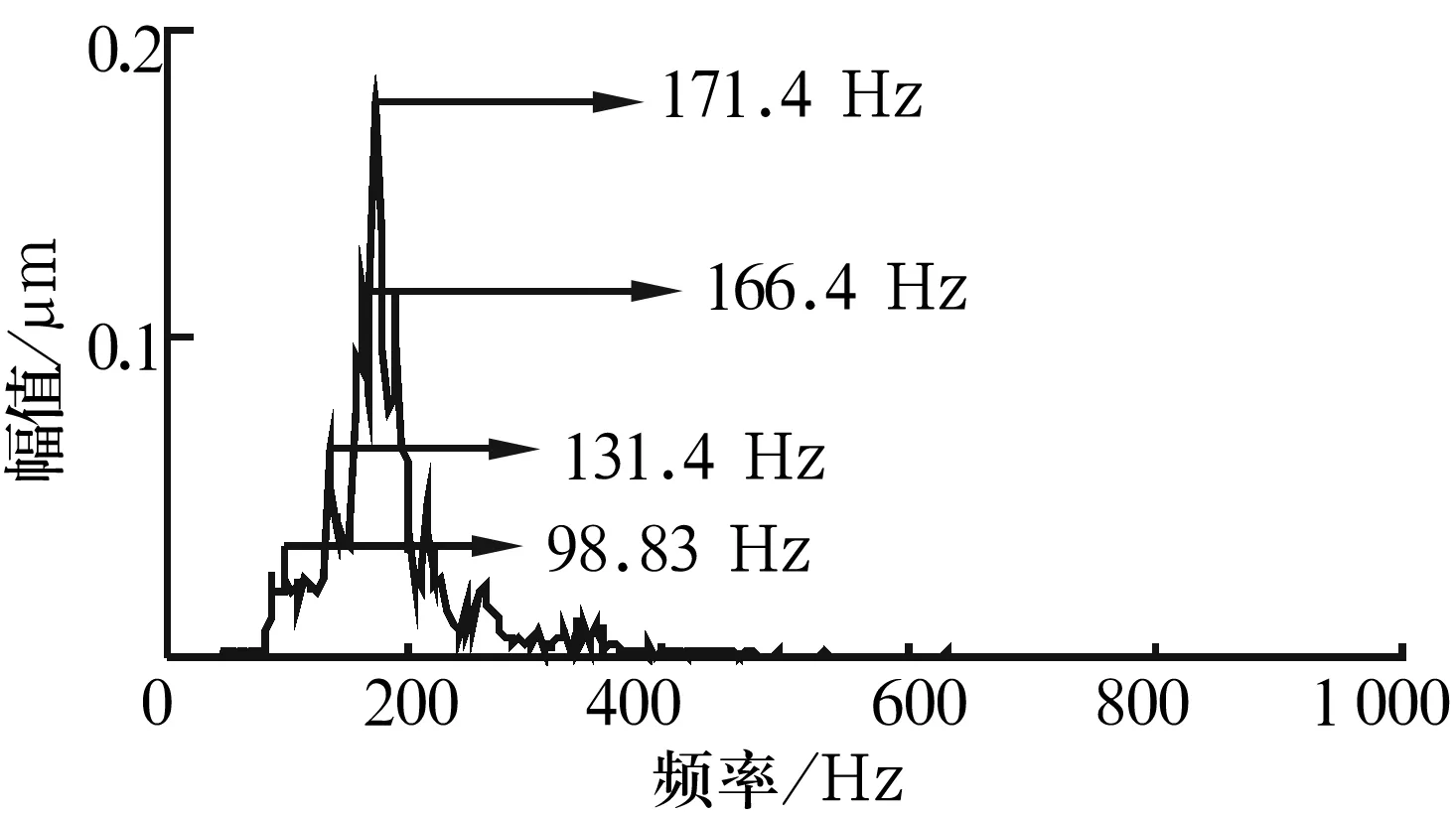
圖5 未經諧波小波濾波信號的Hilbert邊際譜
由圖5可以看出,頻率上升和下降階段均呈階梯形,出現了大量邊頻,給信號的物理解釋帶來困難,而且故障診斷受到干擾,容易引起誤判。與圖4比較可得,諧波小波濾波可以有效去除干擾頻率,突出信號的主要成分。
2.2 實際應用
針對某變速箱中NU205M軸承實際信號進行分析。其中,軸承外圈有直徑為0.403 mm、深度為0.223 mm的點蝕,控制器頻率設置為40 Hz,振動信號由橫向通道數據記錄儀采集,采樣頻率為10 kHz,實際轉速為1 188.12 r/min。計算可知軸承外圈故障頻率為104 Hz,波形如圖6所示。
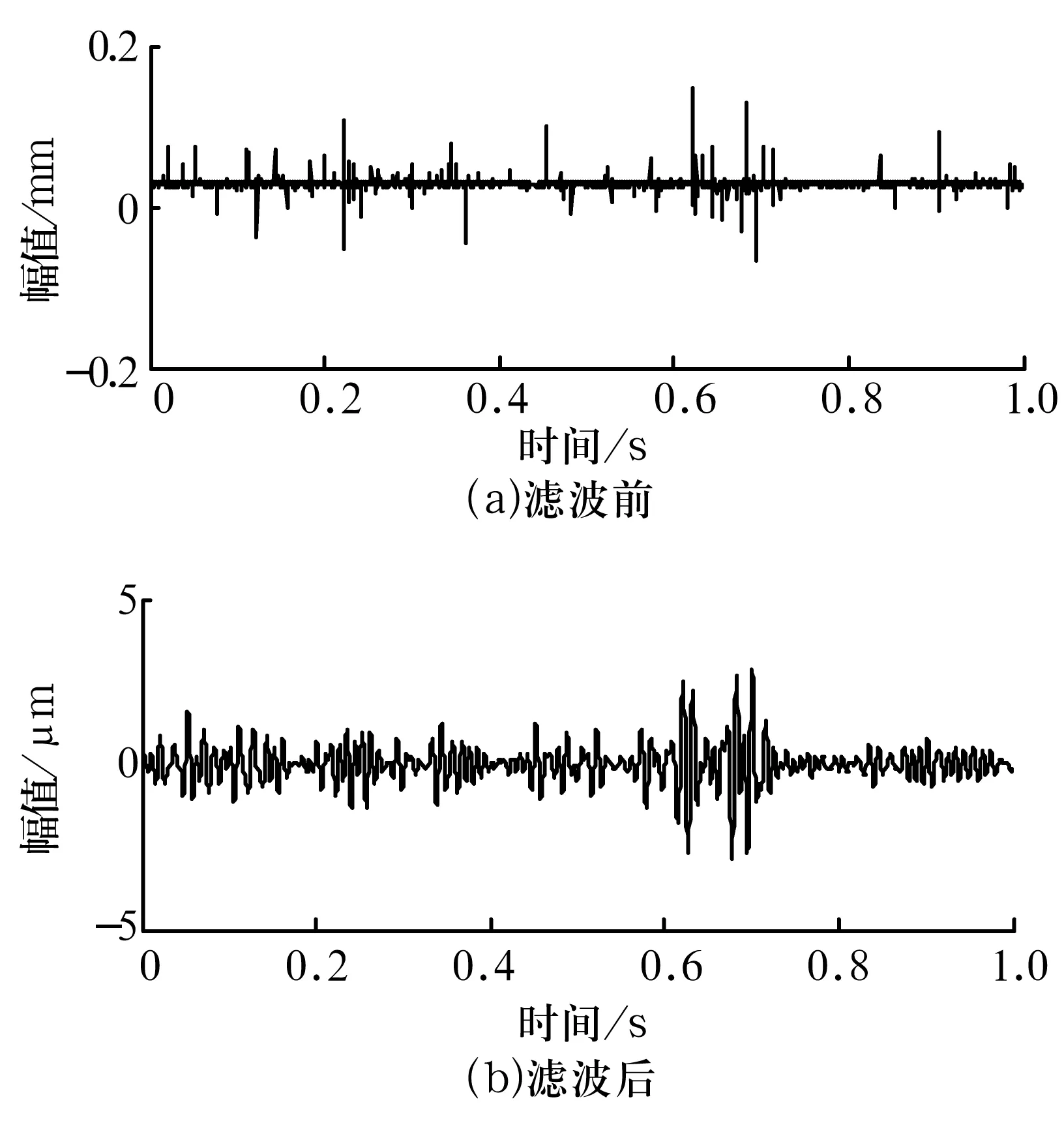
圖6 實際外圈故障信號的時域波形
經過諧波小波濾波處理后,由圖5b可以看出,諧波小波濾波器有效地消除了干擾噪聲,提高了信噪比,圖中的振動信號呈現有規律的波動。對濾波后的信號進行EMD處理,如圖7所示。
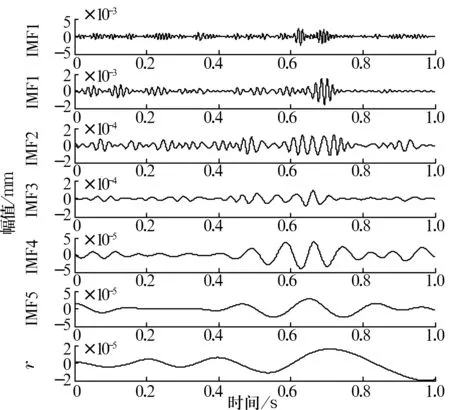
圖7 EMD處理后的軸承信號
經諧波小波濾波處理后,對特定信號頻率段IMF1進行邊際譜分析,結果如圖8所示。從圖中可以清楚看出峰譜值為107.4 Hz,診斷為外圈故障,與實際情況相符。
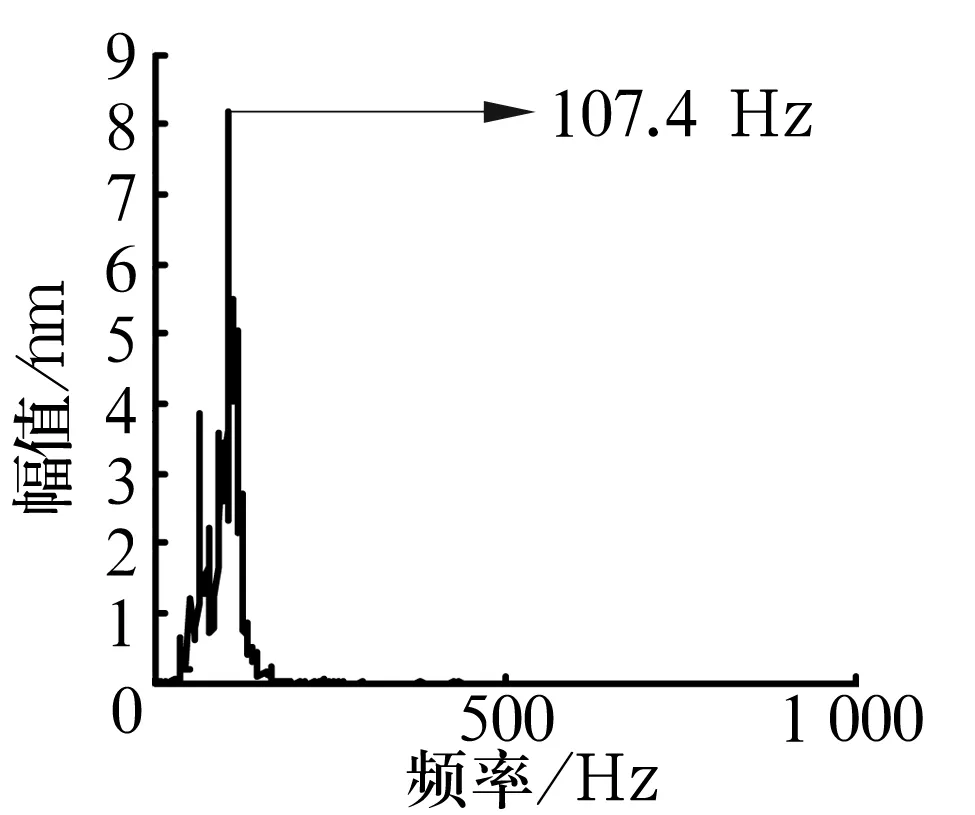
圖8 外圈故障軸承Hilbert邊際譜
另一NU205M軸承存在內圈故障,為直徑0.32 mm、深0.217 mm的點蝕,控制器頻率設置為20 Hz,振動信號由橫向通道數據記錄儀采集,采樣頻率為4 kHz,實際轉速為589.68 r/min。計算可知軸承內圈故障頻率為76.167 Hz。經諧波小波濾波處理后,對特定信號頻率段作邊際譜分析,結果如圖9所示。從圖中可以清楚看出峰譜值為74.8 Hz,診斷為內圈故障,與實際情況相符。
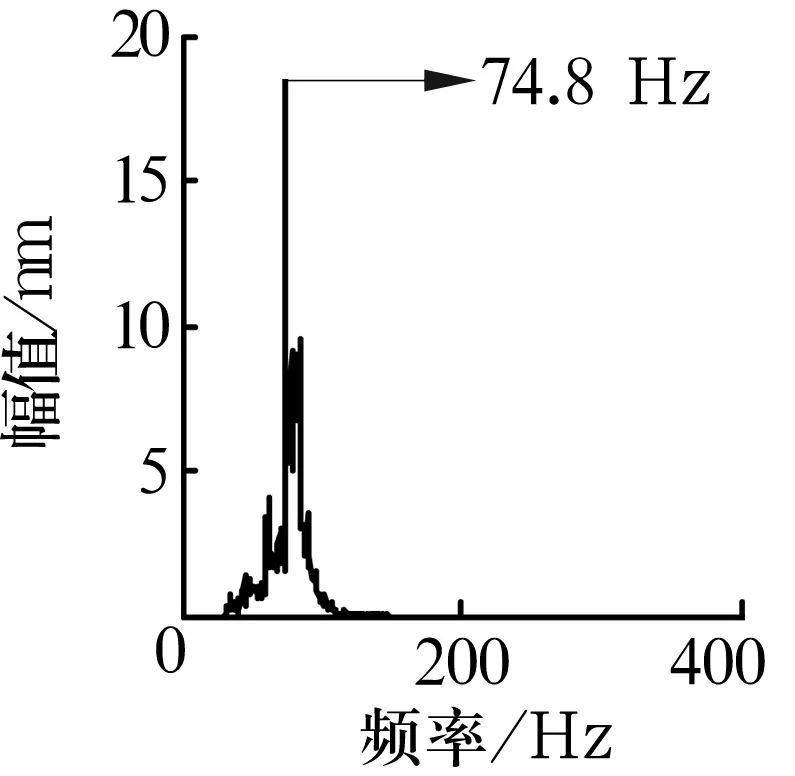
圖9 內圈故障軸承Hilbert邊際譜
3 結束語
將諧波小波濾波與HHT相結合,應用到滾動軸承故障診斷中,實例分析表明,該方法能有效去除干擾噪聲,突出噪聲環境下軸承振動信號的數據特征,進而提取故障信號的特征成分,具有實用價值。

