交換環(huán)上低階反對稱矩陣?yán)畲鷶?shù)的李三導(dǎo)子

彭曉霞，陳海仙，王 穎

(大連理工大學(xué)數(shù)學(xué)科學(xué)學(xué)院，遼寧 大連 116024)

交換環(huán)上低階反對稱矩陣?yán)畲鷶?shù)的李三導(dǎo)子

彭曉霞，陳海仙，王 穎

(大連理工大學(xué)數(shù)學(xué)科學(xué)學(xué)院，遼寧 大連 116024)

設(shè)R是含1的交換環(huán)，用Un(R)(n∈N+)表示R上的n階反對稱矩陣?yán)畲鷶?shù).研究了U4(R)及U5(R)上的李三導(dǎo)子，并證明了它們的李三導(dǎo)子都是內(nèi)導(dǎo)子.同時也說明了U4(R)及U5(R)都是完備李代數(shù).

反對稱矩陣；李三導(dǎo)子；內(nèi)導(dǎo)子；交換環(huán)；完備李代數(shù)

1 預(yù)備知識

近些年來，許多學(xué)者都研究過一般線性李代數(shù)及其子代數(shù)的導(dǎo)子，并且取得了一些重要成果.[1-8]如：文獻(xiàn)[1]刻畫了交換環(huán)上嚴(yán)格上三角矩陣?yán)畲鷶?shù)的導(dǎo)子；文獻(xiàn)[2]刻畫了三角矩陣上的李導(dǎo)子；文獻(xiàn)[3]刻畫了一般線性李代數(shù)的拋物子代數(shù)的導(dǎo)子；文獻(xiàn)[4]刻畫了可交換環(huán)上嚴(yán)格上三角矩陣?yán)畲鷶?shù)的李三導(dǎo)子；文獻(xiàn)[5]刻畫了交換環(huán)上嚴(yán)格上三角矩陣的廣義李三導(dǎo)子；文獻(xiàn)[6]刻畫了廣義李三導(dǎo)子的一些性質(zhì).關(guān)于反對稱矩陣?yán)畲鷶?shù)的李三導(dǎo)子，目前還沒有什么結(jié)果.本文旨在描述交換環(huán)上低階反對稱矩陣?yán)畲鷶?shù)的李三導(dǎo)子.在定理的證明中我們使用了大量的矩陣技巧來得到一些有用的等式.

設(shè)R是含1的交換環(huán)，Un(R)(n∈N+)是R上的n階反對稱矩陣構(gòu)成的集合.定義[A，B]=AB-BA，?A，B∈Un(R)，則Un(R)關(guān)于[，]運算構(gòu)成李代數(shù)，稱其為R上的n階反對稱矩陣?yán)畲鷶?shù).

定義1[4]設(shè)ρ：Un(R)→Un(R)是一個線性變換，若對任意的A，B∈Un(R)，都有ρ[A，B]=[ρ(A)，B]+[A，ρ(B)]，則稱ρ為Un(R)上的一個導(dǎo)子.

定義2[4]若一個線性變換φ：Un(R)→Un(R)滿足

φ([[a，b]，c])=[[φ(a)，b]，c]+[[a，φ(b)]，c]+[[a，b]，φ(c)]，?a，b，c∈Un(R)，

則稱φ為Un(R)上的一個李三導(dǎo)子.

定義3[8]設(shè)Z∈Un(R)，如果對任意的A∈Un(R)，都有[Z，A]=0，則稱Z為Un(R)的中心元素.Un(R)的所有中心元素的集合稱為Un(R)的中心.

注1 導(dǎo)子一定是李三導(dǎo)子，但反之不一定成立.

關(guān)于交換環(huán)上低階反對稱矩陣?yán)畲鷶?shù)的李三導(dǎo)子，本文給出了以下結(jié)果：

設(shè)φ和φ分別是U4(R)，U5(R)上的李三導(dǎo)子，則φ和φ都是內(nèi)導(dǎo)子.

2 定理的證明

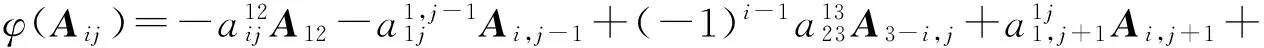
證明 由[[A12，A13]，A12]=A13，可知

[[φ(A12)，A13]，A12]+[[A12，φ(A13)]，A12]+[-A23，φ(A12)]=φ(A13)，

又[[A1j，A12]，A1j]=A12，j=3，4.于是有

[[φ(A1j，A12]，A1j]+[[A1j，φ(A12)]，A1j]+[A2j，φ(A1j)]=φ(A12)，

由于[[A12，A13]，A14]=0，因此

[[φ(A12)，A13]，A14]+[[A12，φ(A13)]，A14]+[-A23，φ(A14)]=0，

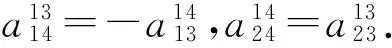
由[[A12，A23]，A13]=0及[[A23，A12]，A23]=A12，可得

因為[[A13，A23]，A14]=A24，所以

根據(jù)[[A23，A12]，A14]=A34，可知

故結(jié)論得證.

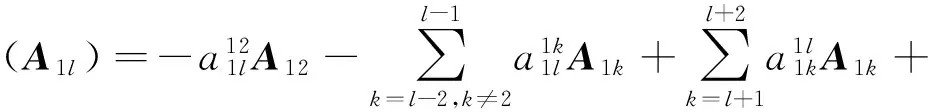
其中：i=2，3；j=4，5；3≤l≤5.

證明 由[[A12，A1l]，A12]=A1l，3≤l≤5，可知

[[φ(A12)，A1l]，A12]+[[A12，φ(A1l)]，A12]+[-A2l，φ(A12)]=φ(A1l)，

因此

因為

[[A1l，A12]，A1l]=A12，3≤l≤5，

所以

[[φ(A1l)，A12]，A1l]+[[A1l，φ(A12)]，A1l]+[A2l，φ(A1l)]=φ(A12).

于是有

由[[A12，A13]，A1j]=0，4≤j≤5及[[A12，A14]，A15]=0，可得

因此

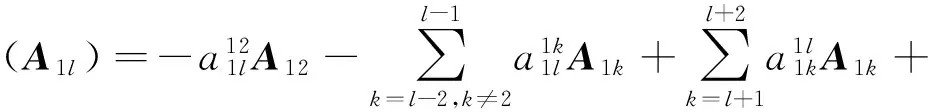
由[[A12，A23]，A23]=-A12可知，

根據(jù)[[A12，A13]，A23]=0，我們有

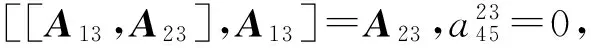
因為

[[A13，A1j]，A23]=A2j，4≤j≤5，

由上述證明的結(jié)論有

又[[A1j，A12]，A23]=A3j，4≤j≤5，因此

由[[A12，A14]，A25]=A45，可得

綜上所述，所證結(jié)論成立.

由上述引理，我們易得下面的定理.

定理1 設(shè)φ和φ分別是Un(R)，n=4，5上的李三導(dǎo)子，則φ和φ都是內(nèi)導(dǎo)子.

證明 不妨設(shè)

當(dāng)n=4時，令

則由引理1，(φ-adx)(Aij)=0，因此φ=adx.

當(dāng)n=5時，令

則(φ-ady)(Aij)=0.因此φ=ady，故所證命題成立.

易知，U4(R)，U5(R)的中心為{0}，所以我們有下面的推論.

推論1U4(R)，U5(R)都是完備李代數(shù).

[1] OU SHIKUN，WANG DENGYIN，YAO UIPING.Derivations of the Lie algebra of strictly upper triangular matrices over a commutative ring[J].Linear Algebra Appl，2007，424：378-383.

[2] DOMINIK.Lie derivations on triangular matrices[J].Linear and Multilinear Algebra，2007，55(6)：619-626.

[3] WANG DENGYIN，YU QIU.Derivaions of parabolic subalgebras of the general linear Lie algebra over a commutative ring[J].Linear Algebra Appl，2006，418：763-774.

[4] HENG'TAI WANG，QING'GUO LI.Lie triple derivation of the Lie algebra of strictly upper triangular matrix over a commutative ring[J].Linear Algebra Appl，2009，430：66-77.

[5] LI HAI-LING，WANG YING.Generalized Lie triple derivations of strictly upper triangular matrices over a commutative ring[J].J of Math，2012，32(2)：254-262.

[6] LI HAI'LING，WANG YING.Generalized Lie triple derivations[J].Linear and Multilinear Algebra Appl，2011，59(3)：237-247.

[7] 李小朝，陳瑩.一類矩陣?yán)畲鷶?shù)的結(jié)構(gòu)[J].東北師大學(xué)報：自然科學(xué)版，2012，44(2)：14-17.

[8] JAMES E HUMPHREYS.Introduction to Lie algebras and representation theory[M].New York：Springer，1997：6-7.

Abstract:LetRbe a commutative ring with identity 1.Denote byUn(R)(n∈N+) the Lie algebra consisting of alln×nantisymmetric matrices overR.This article describes the Lie triple derivations ofU4(R) andU5(R)，and proves that their Lie triple derivations are inner derivations.As application，we prove thatU4(R) andU5(R) are perfect Lie algebra.

Keywords:antisymmetric matrices；Lie triple derivation；inner derivation；commutative ring；perfect Lie algebra

(責(zé)任編輯：陶 理)

Lie triple derivations of the Lie algebra of antisymmetric matrices of low dimensions over a commutative ring

PENG Xiao-xia，CHEN Hai-xian，WANG Ying

(School of Mathematical Sciences，Dalian University of Technology，Dalian 116024，China)

1000-1832(2014)03-0016-04

10.11672/dbsdzk2014-03-004

2013-05-06

國家自然科學(xué)基金資助項目(J1103110).

彭曉霞(1990—)，女，碩士研究生；通訊作者：王穎(1967—)，女，博士，副教授，主要從事李代數(shù)研究.

O 152.5 [學(xué)科代碼] 110·21

A