有關奇完全數的一點注記
張四保,劉啟寬
(1.喀什師范學院數學系,新疆 喀什 844008;2.昆明學院數學系,云南 昆明 650214;3.成都信息工程學院數學學院,四川 成都 610225)
1 預備知識
設N是正整數集合,設σ(n)是正整數n所有不同正約數(包括1和其自身)的和函數.如果正整數n滿足σ(n)=2n,則n被稱為完全數.此時,若n是偶數,則n被稱為偶完全數;若n是奇數,則n稱為奇完全數.到目前為止,只發現了48個偶完全數,而尚未找到奇完全數,也未能給出其存在與否的合理性證明.是否存在奇完全數是數論中一個盡人皆知的沒有解決的問題.[1]
奇完全數存在性問題雖尚未解決,但其有著眾多的研究熱點,如相異素因數個數的下界估計與素因數的大小估計,以及奇完全數的下界大小估計等.對于這些有關奇完全數的熱點問題的研究情況,可參見文獻[3-8].
對于奇數而言其個位數字必是1,3,5,7,9中之一.而對于奇完全數的各個位次上數字的取值情況,以及取值條件的確定,對奇完全數存在的問題具有一定的促進作用.本文通過對奇完全數的Euler因子以及非Euler因子及其指數的討論,利用中國剩余定理對n的個位數字進行探討.
為了敘述的方便,現對一些符號加以說明:
(1)ordp(n)表示一個非負有理數s,使得ps整除n,而ps+1不整除n;
(2)[x]表示不超過實數x的最大整數;
2 主要結論及證明
引理1 令π為給定奇完全數n的歐拉素因子,則有πordπ(n)≡π(mod 5).
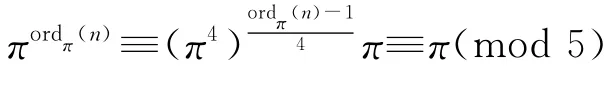
證明 如果π=5,則證明是平凡的.現在令π≠5,因為ordp(n)是偶數,所以
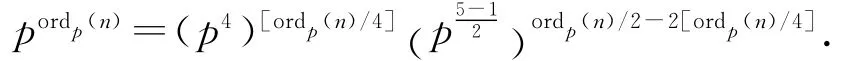
由費馬小定理及Legendre符號的定義,有
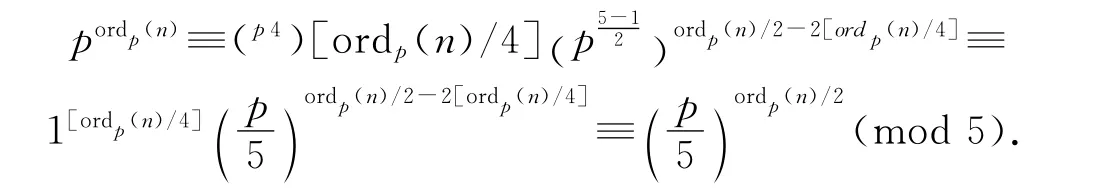
故引理2得證.
定理1 令π為給定奇完全數n的歐拉素因子,則有
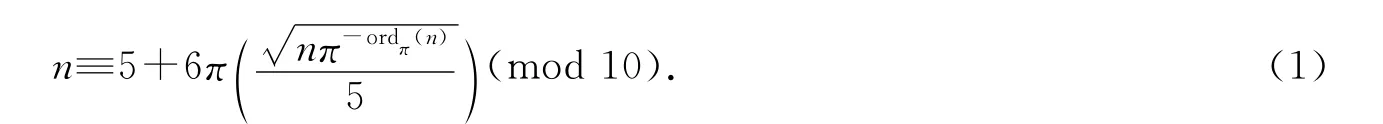
[1]蓋伊R K.數論中未解決的問題[M].第二版.張明堯,譯.北京:科學出版社,2006:59.
[2]EULER L.Commentationes arithmeticae collectae[J].Tractayus de Numerorum Doctrina,1849,2:515-517.
[3]HAGIS P.Outline of a proof that every odd perfect number has eight prime factors[J].Math Comp,1980,35:1027-1032.
[4]NIELSEN P P.Odd perfect numbers have at least nine distinct prime factors[J].Math Comp,2007,76:2109-2120.
[5]ZHANG SIBAO,DENG YOUNG.Numberω(n)of distinct prime factors for a kind of odd perfect number[J].中國科學院研究生院學報,2011,28(4):548-550.
[6]VOIGHT J.On the nonexitence of odd perfect numbers[J].MASS Selecta,2003:293-300.
[7]GOTO T,OHNO Y.Odd perfect numbers have a prime factor exceeding 108[J].Math Comp,2008,77:1859-1868.
[8]COHEN G L,SORLI R M.On the number of distinct prime factors of odd perfect number[J].Journal of Discrete Algorithms,2003(1):21-35.

