局部環(huán)上n階矩陣的{1}-逆作成的群

吳 炎，楊其強

(瓊州學院理工學院，海南 三亞 572022)

局部環(huán)上n階矩陣的{1}-逆作成的群

吳 炎，楊其強

(瓊州學院理工學院，海南 三亞 572022)

研究了有單位元的可換局部環(huán)上n階可對角化的矩陣A的{1}-逆集中的子群及其構造問題，運用矩陣和群方法，給出了這個矩陣A的{1}-逆集AP{1}-中元素的乘法封閉的條件，獲得了矩陣A的{1}-逆集AP{1}中的子集作成群的充要條件，以及這些子群的結構定理及相關結果.

可換局部環(huán)；廣義逆矩陣；矩陣群；LU分解

1 預備知識

矩陣廣義逆的應用十分廣泛，在統(tǒng)計學、控制工程、力學、生物學等諸多領域都有較好的應用.如文獻[1]利用{1}-逆等解決了水果模糊圖像的恢復問題.近年來許多學者在自反廣義逆的逆反律、分塊矩陣廣義逆的塊獨立性、廣義逆的線性組合、推廣形式的矩陣及其結構和性質等交叉拓展方面開展了研究，也做了不少工作[2-11].最近我們曾在文獻[5]中初步討論了廣義逆矩陣半群中的子集及其元素的一些性質，在本文中我們將進一步研究n階矩陣A的{1}-逆集AP{1}中的矩陣子群的存在和構造及相關問題，通過運用矩陣和群方法，得到了矩陣A存在{1}-逆且其{1}-逆的乘法封閉的條件，以及集合AP{1}中子集關于其乘法作成群的充要條件及相關結構，推廣了矩陣群和矩陣廣義逆的相關理論.

文中假設R是有單位元1的可換局部環(huán)，m是R的唯一極大理想，用R*=R-m表示R中可逆元乘法群，用Z+表示正整數(shù)集，Mn(R)(或Mn(m))表示元素在R(或m)中的所有n階矩陣構成的集合，GLn(R)表示R上n階一般線性群，用I(n)和0(n)分別表示n階單位矩陣和n階零矩陣.用H≤G表示群H是群G的子群.易見，若設t∈R；a∈R*；u，b∈m；A∈GLn(R)；B∈Mn(R)；D∈Mn(m).則有a±u∈R*；b±u，tu∈m；A±D∈GLn(R)；tD，bA∈Mn(m).若是a∈R，a2=a，則有a=0或a=1.因此，若U=diag{d1，…，dn}(di∈R*，i=1，…，n)，且U2=U，則有di=1(i=1，2，…，n)，U=I(n).

我們知道，若假設A∈Mn(R)，則把滿足矩陣方程

AXA=A

(1)

的矩陣X(∈Mn(R))稱為A的{1}-逆，這里用A{1}表示A的所有{1}-逆矩陣所構成的集合.

2 n階可對角化矩陣存在{1}-逆且其{1}-逆的乘法封閉的條件

假設A(∈Mn(R))是一個可對角化的矩陣，即

PAP-1=diag{U，D，0}=C.

(2)

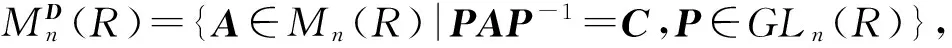
特別當(2)式中的D=0，U=I(r)時，A的任意一個{1}-逆矩陣X為

其中：X12∈Mr×(n-r)(R)，X21∈M(n-r)×r(R)，X22∈Mn-r(R).

由引理2.1，可設A=P-1diag{U，0(n-r)}P，U=diag{d1，…，dr}∈GLr(R)，且

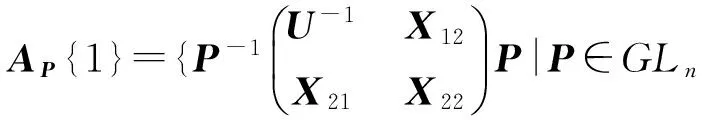
引理2.2 設A=P-1diag{U，0(n-r)}P，U=diag{d1，…，dr}∈GLr(R)，且

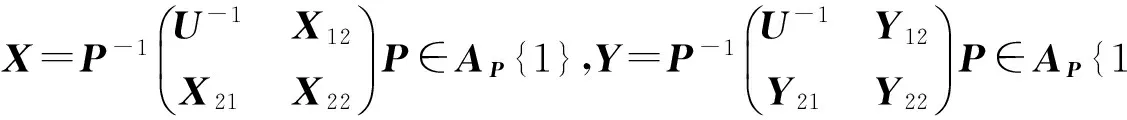
(3)

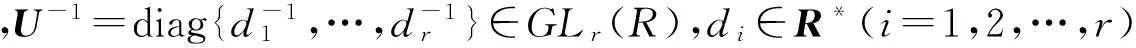
XY∈AP{1}?(U-1)2+X12Y21=U-1.

特別的，當U=I(r)時(此時U-1=I(r))，則上式右邊(U-1)2=U-1=I(r)，于是有

XY=AP{1}?X12Y21=0.

證明 由滿足(3)式的X，Y(∈AP{1})，經(jīng)直接計算有

(4)

若XY∈AP{1}，則由(4)式及引理2.1得到(U-1)2+X12Y21=U-1.

反之，如果(3)式所給矩陣X，Y滿足(U-1)2+X12Y21=U-1，則由(4)式及引理2.1有

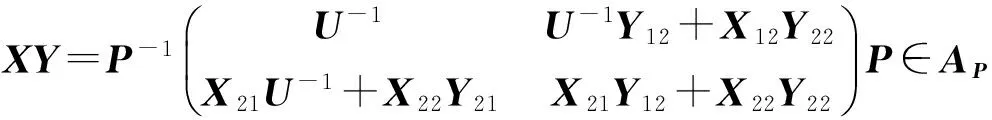
3 AP{1}中的子群及相關結果

我們約定，只討論滿足如下條件的矩陣A(∈Mn(R))：

A=P-1diag{I(r)，0(n-r)}P.

(5)

于是由引理2.1可得

(6)

其中：P是GLn(R)中取定不變的可逆矩陣，X12∈Mr×(n-r)(R)，X21∈M(n-r)×r(R)，X22∈Mn-r(R).

引理3.1[5]設A=P-1diag{I(r)，0(n-r)}P，且

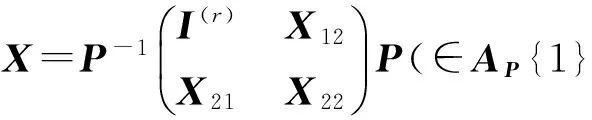
(7)

(8)

(9)

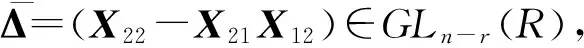
則顯然有Y∈AP{1}.由于有

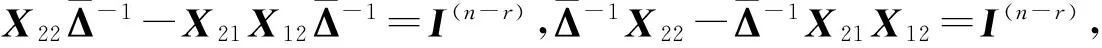
(10)

(11)

(12)

(13)

同理可得YX=I，于是(7)式中的矩陣X可逆且X-1=Y∈AP{1}∩GLn(R).

定理3.1 設A=P-1diag{I(r)，0(n-r)}P，且

如果對于任意X，Y∈H有XY∈AP{1}，那么H對于其矩陣的乘法作成一個群.

證明 由引理3.2可知H?AP{1}∩GLn(R)，又顯然有I=P-1diag{I(r)，I(n-r)}P∈H≠?，且對任意X∈H有IX=XI=X，故要證明H是一個群，只需證明以下兩點：

(1) 對于任意X∈H，都有X-1∈H.

事實上，對于任意X∈H，由H中元素所滿足的條件及引理3.2得到X，X-1∈AP{1}∩GLn(R)，且

(14)

(2) 對于任意X，Y∈H，有XY∈H.

對于任意X，Y∈H?AP{1}∩GLn(R)，由H中元素所滿足的條件及結論(1)，有X-1，Y-1∈AP{1}∩GLn{R}.又由已知條件有XY∈AP{1}，而易見XY∈GLn(R)，故XY∈AP{1}∩GLn(R)，于是可設

推論3.1 設H是定理3.1確定的群，則AP{1}中如下子集對于其矩陣乘法作成H的子群：

證明 只需證(1)中H(X12)≤H(X12∈Mr×(n-r)(m))，其余同理可證.事實上，對于任意

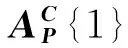
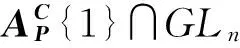
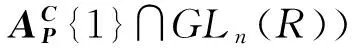
(15)

(16)

由(15)和(16)式中L，U構作

K={L1U1|L1∈L，U1∈U，U-1L-1∈AP{1}}.

(17)

則由推論3.2的結論(1)有L≤H，U≤H，且易見K?AP{1}∩GLn(R).因此有下面的結論.

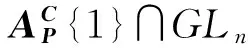
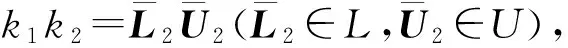
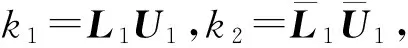
(18)

由此，經(jīng)直接計算得到

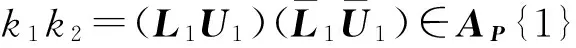
(19)

(20)

故有U2∈U，也有

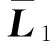
(21)

(22)

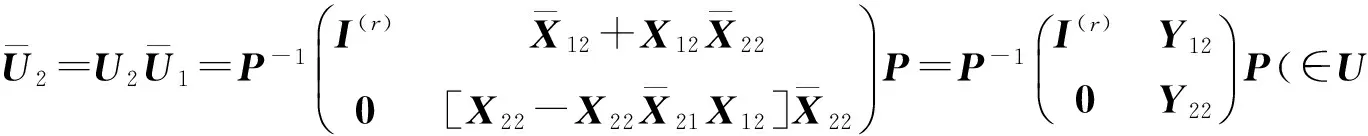
(23)

此外，由(22)式和(23)式還得到

(24)

(25)

(26)

(2) 顯然I∈L，I∈U，I-1I-1=I∈AP{1}，故單位矩陣I=I·I∈K≠?，且K?GLn(R).故要證明，在所給條件下K對其乘法作成群，且K=H，只需證明以下幾點：

由(18)式中所給的L1和U1經(jīng)直接計算得到：

(27)

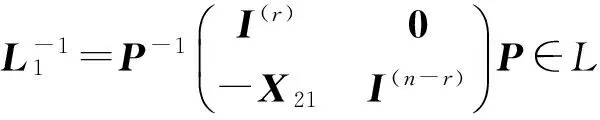
(28)

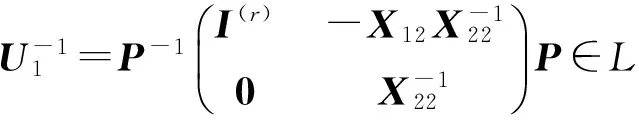
(29)

于是有

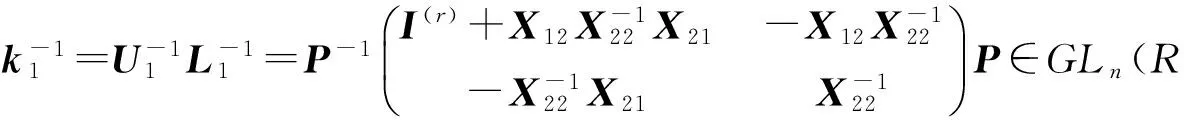
(30)

(31)

(32)

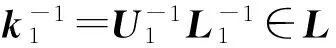
(Ⅲ) 最后證明，H?K，K=H.事實上，對于任意X∈H，可設

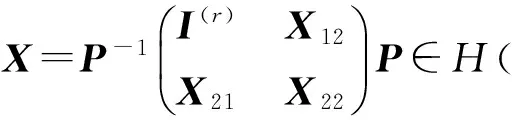
(33)

(34)

其中

(35)

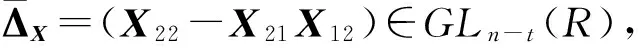
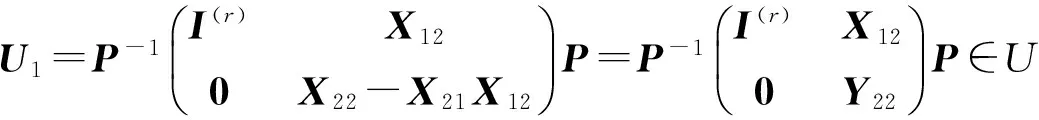
(36)

綜合(Ⅱ)，(Ⅲ)的證明有H=K.

[1] 桂江生，應義斌.基于矩陣廣義逆和奇異值分解的運動水果模糊圖像恢復[J].生物數(shù)學學報，2006，21(1)：448-452.

[2] SHINOZAKI N，SIBUYA M.Further results on the reverse order law[J].Linear Algebra Appl，1979(27)：9-16.

[3] HONG YOU，JIANLONG CHEN.Generalized inverses of a sum of morphisms[J].Linear Algebra and its Applications，2001(338)：261-273.

[4] 劉淑丹，游宏.域上矩陣積的廣義逆及自反廣義逆的逆反律[J].數(shù)學年刊：A，2004，25(4)：523-530.

[5] 吳炎，張宗杰，符曉芳.局部環(huán)上矩陣廣義逆半群的子集及其性質[J].數(shù)學的實踐和認識，2011，41(6)：168-174.

[6] 袁暉坪.關于k-廣義Hermite矩陣的研究[J].東北師大學報：自然科學版，2012，44(2)：5-8.

[7] 章里程，廖祖華.分塊矩陣加權逆的塊獨立性[J].數(shù)學雜志，2010，30(5)：921-925.

[8] 吳炎.局部環(huán)上冪等矩陣線性組合的廣義逆之間的關系[J].純粹數(shù)學與應用數(shù)學，2012，28(2)：155-166.

[9] 吳炎，邱發(fā)儒，易文靜.相似變換下方陣的拓展{I}-逆及其應用[J].河南大學學報：自然科學版，2010，40(6)：565-570.

[10] 盛中平.多項式系的子結式矩陣[J].東北師大學報：自然科學版，2013，45(2)：1-4.

[11] 吳炎.相似變換下冪零矩陣的{2，3}-逆的表示式[J].瓊州學院學報，2013，20(5)：19-25.

Abstract:In this paper，we study the subgroups of the setAP{1} formed by some {1}-inverses of diagonalization matrixAof ordernover a commutative local ring with an identity and their structures.By using the methods of matrix and group，we give the conditions on the closure of multiplication in the setAP{1}.Furthermore，we also obtain some necessary and sufficient conditions that make the subsets of the setAP{1} into groups and some structure theorems about these subgroups and some relevant results.

Keywords:commutative local ring；generalized inverse matrix；matrix group；LU-decomposition

(責任編輯：陶 理)

Groups of {1}-inverses of matrixAof ordernover a local ring

WU Yan，YANG Qi-qiang

(School of Physics and Engineering，Qiongzhou University，Sanya 572022，China)

1000-1832(2014)03-0028-06

10.11672/dbsdzk2014-03-006

2013-07-31

海南省自然科學基金資助項目(113008).

吳炎(1964—)，男，教授，主要從事矩陣群和矩陣論及其應用研究.

O 151.21 [學科代碼] 110·21

A