利用HPGe鈾能譜88～100 keV能區確定鈾富集度方法研究

周 浩，趙永剛，李建華，金惠民

(中國原子能科學研究院 放射化學研究所，北京 102413)

γ能譜法是測量鈾富集度的首選方法之一，其所用探測器和分析技術取決于應用場景和被測對象。HPGe、NaI(Tl)以及CdTe/CdZnTe是γ能譜測量中常用的3種探測器，其中HPGe探測器能量分辨率最高，最適合進行復雜能譜的精確分析。

與豐度計原理法相比，利用鈾能譜88～100 keV能區重峰解析確定鈾富集度方法具有以下優點：1) 無需使用已知鈾富集度的樣品進行刻度；2) 被測樣品無需滿足“無限厚度”等條件，并且可是任意幾何形狀和化學形態；3) 該方法同樣具有較高的分析精度[1-3]。

一般而言，該方法對樣品質量及活度無特殊要求，但要求樣品內核素均勻分布。為達到較高分析精度，要求能譜在88～100 keV能區內的計數統計性較好。實際測量中，樣品活度、探測器類型、測量幾何條件等都會影響到能譜計數率，因此需根據實際測量條件選擇合適的測量時間。另外，該方法要求探測器在低能區具有足夠高的能量分辨率。國外有研究[4]表明，當探測器在122 keV處能量分辨率優于3%時，才能使用該方法進行能譜重峰解析。經過多年研究，目前國際上已有應用該方法較為成熟的MGAU、MGA++等軟件，這類軟件在應用中要求探測器低能區(100 keV左右)能量分辨率足夠高，并且探測器及譜儀的設置均應滿足其要求。這類軟件中使用的能區內效率修正方法需低能分辨率較高(例如達到0.5%)，對于低能分辨率優于3%,又達不到該要求的HPGe探測器，以及新型的CdTe/CdZnTe探測器，目前尚缺乏合適的解決方法。

本文擬自行編寫一套能適用于大多數HPGe探測器能譜的鈾富集度分析程序，以研究用效率擬合因子進行效率修正的可行性。在解譜程序編寫完成后，對鈾富集度已知的兩種鈾樣品進行實驗測量，檢驗解譜程序的可行性。

1 原理

鈾富集度的計算公式為：

(1)

式中：Enr為鈾富集度；N5、N8、N4和N6分別為235U、238U、234U、236U的原子數。

通常234U和236U的同位素豐度很小(如234U在武器級高濃鈾材料中含量才可能達到1%)，本文將其忽略，235U富集度僅取決于235U和238U的原子數之比。

同一樣品中兩種核素的原子數之比可通過測得的相應特征能峰凈計數之比以及全能峰探測效率之比計算獲得：

(2)

式中：S為特征峰凈面積；Br為分支比；ε為全能峰探測效率；T為半衰期；下標5和8分別表示235U和238U。

選取鈾能譜中88～100 keV能區內的11個主要能峰進行分析，該能區內的能峰組成示于圖1，圖中N為能譜凈計數。這11個γ、X射線能峰分別來自235U的子體231Th及231Pa、238U的子體234Th和U的X射線。231Th半衰期很短(25.5 h)，而234Th半衰期為24 d，新生產的核材料中238U-234Th不平衡，而對于本文測量分析的樣品，生產后已放置半年以上，因此235U-231Th和238U-234Th體系均為衰變平衡體系，可將子體發射的γ射線能峰作為對應母體的特征峰。式(2)中235U和238U各自特征峰的凈面積S5和S8由能譜擬合結果給出。

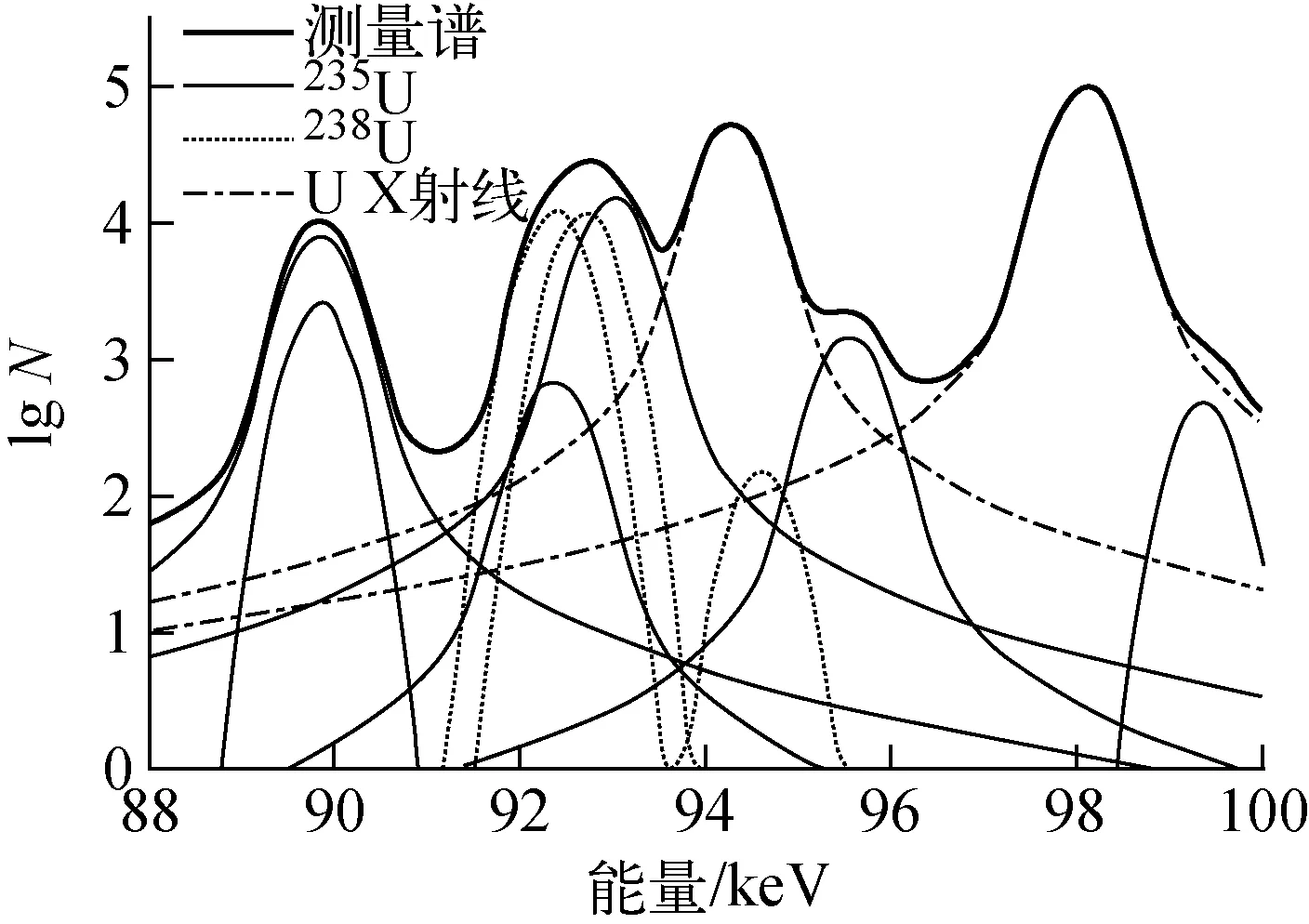
圖1 鈾能譜88～100 keV能區內能峰組成

利用鈾能譜88～100 keV能區重峰解析確定鈾富集度時需考慮能區內的探測效率修正問題，國際上現行的做法是通過104～116 keV Kβ射線能區內能峰信息進行相對效率自刻度[1,3,5-6]或將能區內能峰的探測效率近似相等[7]。而對于能量分辨率能達到該方法的基本要求，但又不足以使用104～116 keV Kβ射線能區進行相對效率自刻度的探測器，如常用的低能分辨率相對較差的HPGe探測器以及近年來發展較快的CdTe/CdZnTe探測器，尚未見到效率修正方法的相關文獻。

2 算法建立

根據上述鈾富集度分析原理，設計解譜流程，并編寫了相應的計算程序。 其中解譜流程示于圖2。

圖2 程序流程圖

2.1 建立峰形模型

由于能峰的凈面積是通過其峰形函數逐道積分計算得到，因此峰形模型曲線與測量譜中各能峰實際分布的符合程度直接影響到解譜結果的分析精度。峰形模型中的主要參數包括峰面積參數、峰寬參數、尾部修正項參數等。

1) γ射線峰形模型的建立

借鑒相關文獻[8-9]的研究成果，建立γ射線峰形模型：

(3)

式中：f(k)表示單個γ射線在能譜中第k道的凈計數；H0為峰高；wg為高斯函數半高寬；E0為截斷因子；k0為能峰中心位置；A和B分別為能峰的“尾部幅度”和“尾部斜率”。

根據該γ射線峰形模型，編寫程序實現γ射線峰形函數及尾部修正項的計算。

2) X射線峰形模型的建立

X射線本身具有一定的能量展寬(服從洛侖茲分布)，因此其峰形函數是洛侖茲分布函數和探測器響應函數(高斯函數)的卷積，即Voigtian函數：

(4)

式中：I(k)為第k道的凈計數，wg和wl分別為高斯分布、洛倫茲分布的半高全寬分量。SVoigtian為式(3)的積分面積。

由于Wilkinson方法計算Voigtian函數值的相對偏差在0.2%以內[10]，因此本文參考該方法近似計算Voigtian函數的值：

(5)

X射線峰形模型中除Voigtian函數部分外，還需要加上尾部修正項：

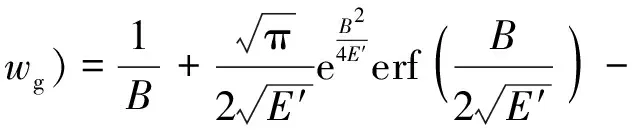
(6)

式中：Stail為尾部修正項的積分面積；E0為尾部截斷因子。采用辛普森積分公式計算式(6)。

式(5)與式(6)之和即為X射線的峰形模型。

根據上述X射線峰形模型，自行編寫程序實現X射線峰形函數及尾部修正項的計算。

2.2 效率修正

如上文所述，利用104～116 keV能區U的Kβ射線進行相對效率修正需要探測器在低能區的能量分辨率較高，并且過程十分復雜。88～100 keV能區較窄，其中各能峰全能峰探測效率差異較小，并且只需要得出不同射線間全能峰探測效率之比即可進行相對效率修正。因此，本文依據相對效率自刻度原理及平滑曲線在窄區間內近似線性變化的特點，假設88～100 keV能區內各能峰的全能峰效率呈線性變化，并且令其中98.4 keV能峰的相對探測效率為1，能量最小的能峰相對探測效率為ε0(也稱為效率擬合因子，其值作為未知量由擬合結果給出)，則能區內其他能峰相對于98.4 keV能峰的相對效率可由內插(或外推)法得到：

(E-98.4)

(7)

式中，εr(E)表示能量為E的能峰對應的相對效率。

由于ε0描述的是能區左右兩端的全能峰探測效率之比，因此可以預期，對幾何、化學形態相同的樣品，在相同測量條件下，分析結果給出的效率擬合因子ε0應當是相近的；而不同類型的樣品，由于其自吸收等因素的影響不同，ε0可能不同，并且其值越小表明能區兩端探測效率差異越大，進行效率修正對提高分析結果的精度意義越大。

3 實驗驗證

3.1 實驗材料

供分析測量的有兩類樣品：U3O8粉末和UO2核燃料芯塊。U3O8粉末樣品的鈾富集度分別為4.06%(2.3 g)、19.9%(1.3 g)、36.8%(3.3 g)、90.1%(1.9 g)；UO2核燃料芯塊樣品的鈾富集度分別為1.80%(1.4 g)、3.20%(1.4 g)、4.20%(1.4 g)、10.0%(1.4 g)。粉末樣品用厚約2 mm的圓底聚乙烯盒盛裝，芯塊樣品無外包裝。這些樣品的標稱值來自質譜法的分析結果，其相對不確定度小于0.5%。

3.2 實驗方法

利用低本底(探測器探頭置于15 cm厚的鋼鉛屏蔽體內)HPGe γ譜儀(GEM100210，相對效率約115%，122 keV處能量分辨率約1%)對粉末、核燃料芯塊兩種類型的8個樣品進行測量和分析。測量過程中保持譜儀高壓、成形時間等參數設置不變，譜儀道寬設置為0.125 keV/道。

被測樣品緊貼探測器端面進行近距離測量，每個樣品的測量時間為2 h，每個樣品重復測量8次以上。另外，將樣品置于距離探測器16 cm處進行重復測量，以分析比較不同測量距離對能區內能峰探測效率差異的影響(測量時間2 h，重復測量8次以上)。

4 結果與討論

實際能譜的典型擬合效果圖如圖3所示(以鈾富集度36.8%的粉末樣品為例，圖中數據點的誤差取其相對標準偏差,下同)。由圖3可看出，擬合譜和測量譜符合程度較高，說明解譜程序中所建立的峰形模型能較好地描述實際峰形。

圖3 能譜的典型擬合效果圖

解譜程序對各樣品重復測量能譜的主要分析結果列于表1。由表1可知，效率近似時，分析結果整體偏小，精度較差，而在進行效率修正后，分析精度明顯提高。效率修正后，芯塊樣品分析值與標稱值的相對偏差在2%以內，其平均值的相對標準偏差低于3%；粉末樣品分析值與標稱值的相對偏差不超過1%，其平均值的相對標準偏差不超過1%。若取包含因子k=2，則芯塊和粉末樣品分析結果各自的相對擴展不確定度分別在6%和2%以內。

表1 兩種類型樣品的分析結果

粉末樣品和芯塊樣品的分析精度及其不確定度(以相對標準偏差進行A類不確定度評定)略有差異，部分原因可能是樣品本身活度、探測效率等差異導致在相同測量時間內的能譜計數統計性不同。表1數據表明，重復測量有效減小了平均值與標稱值的相對偏差。近距離測量時，對芯塊樣品，分析結果給出的效率擬合因子為0.694±0.008(包含因子k=2，置信度95%，下同)，而粉末樣品為0.847±0.010。分析結果給出的效率因子在平均值附近小范圍波動，表明本文采取的效率修正方法穩定性較強。芯塊樣品給出的效率擬合因子小于粉末樣品，說明芯塊樣品能譜中88～100 keV能區兩端的效率差異較粉末的大，可能的原因是其對γ、X射線的自吸收較大。事實上，效率修正后芯塊樣品的分析精度提高更為明顯，這和其效率因子較小相符。

樣品距離探測器16 cm測量時，能譜分析結果給出的效率擬合因子如圖4所示，對于芯塊樣品，分析結果給出的效率擬合因子為0.682±0.016，而粉末樣品的為0.848±0.014。

由于全能峰探測效率與測量距離近似呈反比，探測效率對測量距離的變化十分敏感，而在不確定度范圍內，兩種不同測量距離下的效率因子基本一致，說明探測效率的變化對88～100 keV能區兩端的探測效率影響不大，而主要受樣品本身幾何、化學形態等的影響。

圖4 距離16 cm測量時的效率擬合因子

從效率擬合因子的數值來看，擬合能區(88～100 keV)盡管只有12 keV范圍，但能區兩端的全能峰探測效率差異仍較為明顯，為提高分析精度，有必要采取相應方法進行效率修正。

與國際現有的效率修正方法相比，本文提出的用效率擬合因子修正效率的方法不需要通過能譜中104～116 keV能區進行相對效率自刻度修正，因此適用于所有達到基本分辨率要求的探測器。

5 結論

為利用鈾能譜中88～100 keV能區內的混合γ、X射線的重峰分解確定235U的富集度，自行編寫了鈾富集度解譜程序，在程序中建立了γ、X射線峰形模型、提出用效率擬合因子修正效率的方法，并對解譜程序的可行性進行了實驗驗證。分析結果表明，本文所建立的模型能較好描述實際峰形，提出的效率修正方法可行，整套解譜程序運行穩定可靠。

芯塊樣品測量能譜的程序分析結果與標稱值(由質譜法給出)的相對偏差在2%以內，相對擴展不確定度(k=2)在6%以內；粉末樣品測量能譜的程序分析結果與標稱值的相對偏差在1%以內，相對擴展不確定度(k=2)在2%以內。

參考文獻：

[1] GUNNINK R, RUHTER W, MILLER P, et al. MGAU: A new analysis code for measuring U-235 enrichment in arbitray samples, UCRL-JC-114713[R]. Vienna: IAEA, 1994.

[2] BERLIZOV A, GUNNINK R, ZSIGRAI J, et al. Performance testing of the upgraded uranium isotopics multi-group analysis code MGAU[J]. Nuclear Instruments and Methods in Physics Research A, 2007, 575: 498-506.

[3] MOREL J, HILL C, BICKEL M, et al. Results from the international evaluation exercise for uranium enrichment measurements[J]. Applied Radiation and Isotopes, 2000, 52: 509-522.

[4] LAVIETES A, MCQUAID J, PAULUS T. Cadmium zinc telluride detector system for nuclear material assay[C]∥Institute of Nuclear Materials Management 38thAnnual Meetting. USA: [s. n.], 1997.

[5] BERLIZOV A, TRYSHYN V. Study of the MGAU applicability to accurate isotopic characterization of uranium samples, IAEA-SM-367/14/05/P[R]. Vienna: IAEA, 2001.

[6] CLARK D, WANG T F. Uranium and plutonium isotopic analysis using MGA++, UCRL-JC-131168[C]∥Institute of Nuclear Materials Management 39thAnnual Meeting. Naples, Italy: [s. n.], 1998.

[7] ABBAS K, MOREL J, ETCHEVERRY M, et al. Use of miniature CdZnTe X/γ detector in nuclear safeguards: Characterization of spent nuclear fuel and uranium enrichment determination[J]. Nuclear Instruments and Methods in Physics Research A, 1998, 405: 153-158.

[8] RAY G, WAYNE R. GRPANL: A program for fitting complex peak groupings for gamma and X-ray energies and intensities, UCRL-52917[R]. California: Lawrence Livermore Laboratory, University of California, 1980.

[9] RAY G, ROLF A. Methods for evaluating and analyzing CdTe and CdZnTe spectra[J]. Nuclear Instruments and Methods in Physics Research A, 2001, 458: 196-205.

[10] WILKINSON D. Breit-wingers viewed through Gaussians[J]. Nuclear Instruments and Methods, 1971, 95: 259-264.