基于模糊神經網絡算法的機器人路徑規劃研究

姚毅, 陳光建, 賈金玲

(四川理工學院b.計算機學院;a.自動化與電子信息學院, 四川自貢643000)

基于模糊神經網絡算法的機器人路徑規劃研究

姚毅a, 陳光建b, 賈金玲b

(四川理工學院b.計算機學院;a.自動化與電子信息學院, 四川自貢643000)

路徑規劃是移動機器人研究的關鍵技術之一。在研究模糊理論和神經網絡的基礎上，提出了一種新的算法，即模糊神經網絡。模糊神經網絡既可以像神經網絡那樣并行處理、自行學習，又可以像模糊理論處理模糊信息、完成模糊推理功能。采用模糊神經網絡來對移動機器人的路徑進行規劃，充分發揮模糊理論和神經網絡的各自優勢，從而獲得從起始點到目標點的最優路徑。在環境信息完全未知且靜態的情況下進行了仿真實驗，結果表明：該算法效率高、收斂速度快，有效提高了移動機器人的智能化水平。

移動機器人；路徑規劃；模糊理論；神經網絡

引言

目前，機器人的發展趨勢是高度智能化，而路徑規劃又是評定機器人智能化的重要指標。所謂路徑規劃技術就是當機器人在前進過程中當遇到障礙物無法前進時，需要重新尋找一條路徑到達終點。新找的一條路徑不僅能使機器人繞過障礙物，而且要用時最短，選擇的距離最科學。障礙物的大小，距離機器人的距離都直接影響到機器人的路徑規劃。隨著機器人技術向人工智能化方向的發展，對機器人的路徑規劃提出了越來越高的要求。神經網絡和模糊算法在人工智能方面都表現了各自的優越性，但也存在許多弊端。神經網絡雖然有很好的學習功能及魯棒性，但是它不適合對已經存在的規律性知識的表達，對已有先驗知識不能很好的利用。模糊邏輯能將通常不能用數學方法精確處理的問題用模糊的方法來綜合判斷，但需要全面的先驗知識，來構成推理規則和模糊表。在路徑規劃中，通過模糊算法和神經網絡的有機結合可以很好地綜合各自的優點，使規劃的方式更靈活，規劃的效果更優越。

本文在研究了模糊邏輯算法和神經網絡算法的基礎上，提出了模糊神經網絡算法，并應用于移動機器人的路徑規劃，最后通過了仿真驗證該算法切實可行的。

1 模糊神經網絡

1.1神經網絡

人工神經網絡(Artificial Neural Networks，簡稱ANN)是一種模擬人類大腦的思維能力，通過大量的模擬神經元來實現非線性算法功能的一種網絡。它與人腦神經系統處理信息的過程類似，都具有學習和自適應功能，不同在于其理論基礎是數學網絡拓撲，用神經網絡自身結構表達輸入輸出關系，使網絡具有非線性映射的功能對信息進行并行處理。人工神經網絡主要特點是非線性、能夠并行處理信息的網絡，且具有學習功能、容錯性、信息分布式存儲功能及魯棒性。人工神經網絡的學習規則主要有誤差糾正學習、競爭學習、Hebb學習等。

1.2模糊理論

模糊理論(Fuzzy Theory)是指用到了模糊集合的基本概念或連續隸屬度函數的理論。通過研究發現，模糊邏輯和神經網絡這兩種技術各有所長且具有互補性，因此利用一定的技術將模糊邏輯與神經網絡適當地結合起來，形成一種新的結構，此結構吸取了兩者的長處，且在不失原有特點的基礎上又有自己的特性，是比單獨的神經網絡或單獨的模糊系統性能更好的系統。對于移動機器人路徑規劃這樣復雜的系統，模糊神經控制技術有其巨大的優勢。

1.3模糊系統和神經網絡的融合方式

將神經網絡和模糊邏輯采用一定的手段結合起來形成了一種新結構的技術，叫神經模糊技術。它們的融合主要有神經網絡和模糊系統集成[1]、模糊邏輯增強型的神經網絡、模糊神經網絡三種方式[2-4]。

本文研究的是模糊神經網絡。模糊神經網絡其實就是在傳統的神經網絡中加入了一些模糊成分而形成的。它既可以像神經網絡那樣并行處理、自行學習，又可以像模糊理論處理模糊信息、完成模糊推理功能。根據在神經網絡中加入的模糊成分不同，又可以將模糊神經網絡分成不同類型。模糊神經網絡在保持原有功能的基礎上又有自身的特點。

2 模糊神經網絡的結構及學習算法

2.1模糊神經網絡的結構

模糊推理中的關鍵問題就是隸屬度函數和模糊規則的確定，而基于神經網絡的模糊控制器將它們歸結為神經網絡參數和結構的訓練。有學者提出了基于Takagi-Sugeno模型(簡稱T-S模型)的模糊神經網絡，本文用變結構神經網絡來實現基于T-S的模糊推理[5-9]。

模糊系統的輸出量為每條規則的輸出量的加權平均，即：

(1)

將多個單輸出系統采用一定技術組合起來就形成了一個多輸出系統。現代技術中可以用來實現上述模糊推理過程的典型方法就是神經網絡。

2.2模糊神經網絡的學習算法

模糊神經網絡的學習包含兩個步驟：

第一，參數初調及結構訓練。根據經驗確定網絡參數初值，構造訓練樣本對，進行參數初始學習；然后根據如下規則進行變結構：對于與某個輸出相對應的某個結點j，若與其相連的權均小于某域值，則刪除該結點j。若對于所有的輸出，其對應的結點j都被刪除，則刪除結點j。這表明第j條規則不存在，從而可以實現規則庫的精煉[2]。

第二，進一步進行參數調整。在經過前面的訓練調整后，其網絡結構已經比較成熟，在此基礎之上，讓參數進行再學習。

從本質上來講，由于模糊神經網絡與BP網絡的結構非常類似，因此，其參數學習完全可以借用BP網絡的誤差反傳算法[10-11]。按照T-S模糊系統模型建立了模糊神經網絡，該網絡中的所有結點及相關參數都分別與模糊系統的隸屬函數或者是推理過程對應。該網絡中的參數值隨系統的模糊或定性的知識都是可以根據需要確定的，因為神經網絡是一個黑箱子，參數值要隨機選取；另外，用較短的時間收斂到要求的輸入輸出關系，也是模糊神經網絡的一個優點所在。由于它具有神經網絡的結構，因此，可以實現規則及參數的自學習，與單純的模糊邏輯系統相比，這也是它的優勢所在。

3 機器人對環境的感知

機器人對環境的外部感知采用的是多傳感器信息融合模型，具體結構如圖1所示。

圖1 機器人多傳感器信息融合模型框圖

實現它的核心硬件是智能機器人傳感器交互模塊，該模塊通過串行口和I2C總線配置各個傳感器，包括超聲波、紅外，攝像頭；通過I2C總線連接六組超聲波測距傳感器和四組紅外測距傳感器獲取機器人周圍障礙物信息數據，并利用多傳感器信息融合準確定位障礙物以便機器人實現避障和為返回做準備。用超聲波傳感器和紅外傳感器完成障礙物距離的測量，用視覺傳感器完成障礙物邊緣和位置信息的提取。在對障礙物距離的測量過程中，采用超聲波傳感器測距為主，紅外傳感器為輔，紅外傳感器主要用來彌補超聲波傳感器的一些缺陷，作為緊急避障來使用。

具體的原則為：對CCD攝像頭采集到的視覺信息，按照數字圖像處理的方法檢測到障礙物的邊緣，再利用分區掃描的辦法獲得障礙物邊緣的像素坐標，最后得到障礙物兩側空間的大小，歸一化處理后作為模糊神經網絡輸入[12]。

機器人在作業時主要靠傳感器獲得的外部障礙物信息以及自身所處的狀態來決定下一步該怎樣運動。機器人獲得相關數據通后輸入計算模塊，通過計算得到合理的運動軌跡避開障礙物，且在避開障礙物后，能返回到設定運動路線上繼續前進。

4 模糊神經網絡的訓練

為了減少模糊神經網絡的訓練時間，在此采用了離線訓練[7,13]，其流程如圖2所示。

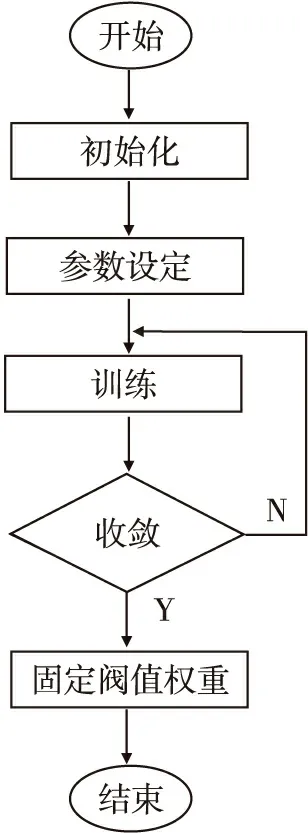
圖2 模糊神經網絡訓練流程圖

根據離線訓練網絡的參數和結構，把已建立的模糊控制規則作為模糊神經網絡控制器的訓練樣本來訓練網絡。在訓練好網絡之后，模糊神經網絡控制器就可以對移動機器人的局部運動進行規劃，通過CCD攝像機、紅外和超聲波傳感器來獲取障礙物信息，從而實現對移動機器人的實時控制。

經過訓練以后，隸屬度函數變得很平緩，即機器人運行比較平穩；當障礙物距離機器人較近時，機器人會實時靈敏的做出相應的操作；當距離較遠時，機器人具有較強的魯棒性控制自己的運動。由此可知：經過訓練，機器人的避障功能得到增強，用于輸入變量的隸屬度函數由于得到有效的優化而更適用于機器人的避障。

5 仿真結果

本仿真實驗是在環境信息完全未知且靜態的情況下進行的。在仿真實驗中，一些外界信息都是通過計算得到的，但是在實際情況中，機器人作業環境的外部信息包括溫度、濕度、障礙物分布情況等都是由傳感器獲得的。為了簡化實驗，在具體操作的時候，將外界信息理想化(比如將障礙物的形狀用圓形來表示)。最后，分別給出了在同樣的環境下障礙物多和障礙物少的路徑圖的兩種仿真結果，其中移動機器人的起始點均為原點。圖3是障礙物分布較密集的時候的路徑軌跡,圖4是障礙物分布較疏散的情況下的機器人仿真路徑。

圖3 障礙物(圓形)較多時的路徑規劃仿真圖

圖4 障礙物(圓形)較少時的路徑規劃仿真圖

通過以上仿真結果可以得出，采樣時間的長短和轉角度數的選擇對機器人路徑規劃有相當重要的影響。仿真結果顯示采樣時間較短時，機器人在障礙物間就會不停地轉向甚至在某些點會打轉進而發生死鎖現象；但當采樣時間比較長時，機器人又會很容易和障礙物發生碰撞，當障礙物較小時機器人還會沖進障礙物區域。本文進行了多次試驗，得到一組能滿足大多數情況的采樣時間和轉角度數的組合：采樣時間0.1秒，轉角度數為5度。由仿真圖可知，機器人可以比較順利地完成路徑規劃，說明采用模糊神經網絡算法是可行的。

6 結束語

本文以已有的機器人雛形為研究對象，針對未知環境下移動機器人路徑規劃問題開展研究。在對神經網絡和模糊理論進行分析對比的基礎上，將兩者有機地結合到了一起，構建了在靜態未知環境下用于路徑規劃的模糊神經網絡，并提出了相應的方法。采用模糊神經網絡對移動機器人的路徑進行規劃，從而獲得從起始點到目標點的最優路徑。該算法能夠有效提高移動機器人的智能化水平。

[1] 許 亮.基于模糊神經網絡的AUV路徑規劃技術[D].青島:中國海洋大學,2007.

[2] 鄭洪濤,李玉榕,喬 斌,等.基于模糊神經網絡開關磁阻電動機轉矩觀測[J].儀器儀表學報,2002,23(4):351-353,360.

[3] 蓋慶書,白 雪.基于神經網絡模型的信息融合技術[J].華北水利水電學院學報,2009(1):25-27.

[4] 叢 爽,戴 宜.遞歸神經網絡的結構研究[J].計算機應用,2004,24(8):18-21.

[5] 周 杰.含擴散項時滯模糊Cohen-Grossberg神經網絡的指數穩定性[J].四川理工學院學報:自然科學版, 2010,23(3):270-274.

[6] 張寒松,賈瑞清.基于實際函數的機器人模糊神經網絡路徑規劃[J].礦山機械,2010,38(14):44-48.

[7] 李貽斌,李彩虹,宋 勇.基于模糊神經網絡的移動機器人自適應行為設計[J].山東大學學報:工學版,2010(2):28-33.

[8] 劉 毅.移動機器人路徑規劃中的仿真研究[J].計算機仿真,2011(6):227-230.

[9] 錢 夔,宋愛國,章華濤,等.基于自適應模糊神經網絡的機器人路徑規劃方法[J].東南大學學報:自然科學版,2012(4):637-642.

[10] 李瑞峰,張 超,黃 超,等.清掃機器人路徑規劃的研究[J].機械設計與制造,2012(12):160-162.

[11] 郜園園,朱凡,宋洪軍.進化操作行為學習模型及在移動機器人避障上的應用[J].計算機應用, 2013(8):2283-2288.

[12] 王華秋.自組織模糊神經網絡的內模控制研究與應用[J].計算機仿真,2014(4):343-346.

[13] 張萬緒,張向蘭,李 瑩.基于改進粒子群算法的智能機器人路徑規劃[J].計算機應用,2014(2):510-513.

Study on the Robot Path Planning Based on Fuzzy Neural Network Algorithm

YAOYia,CHENGuangjianb,JIAJinlingb

(a.School of Automation and Electronic Information; b.School of Computer Science, Sichuan University of
Science & Engineering, Zigong 643000, China)

Path planning is one of the key technologies for mobile robot researches. Based on the study of fuzzy theory and neural network, a new algorithm namely fuzzy neural network is proposed. Fuzzy neural network-FNN can not only perform parallel processing and self learning, as what NNs can do, but also process fuzzy information and perform fuzzy reasoning, as what fuzzy theory can do. The fuzzy neural network-FNN is used for designing routes of mobile robots, and respective advantages of fuzzy theory and NNs are fully utilized, then the optimum route from start point to object point is obtained. In conditions where environmental information is unknown and static, simulation experiment is conducted and the results indicate that this algorithm is efficient and has fast convergence rate, which helps to improve the intelligence level of mobile robots in an efficient way.

mobile robot; path planning; fuzzy theory; neural network

2014-08-01

人工智能四川省重點實驗室基金項目(2014RYY01;2014RYY03);企業信息化與物聯網測控技術四川省高校重點實驗室基金項目(2013WZY02);四川理工學院校級培育科研項目(2012PY21;2013PY06)

姚 毅(1961-),男,四川自貢人,教授,碩士,主要從事信號檢測與智能信息處理方面的研究,(E-mail)yaoyi@suse.edu.cn 陳光建(1979-),男,四川自貢人,副教授,碩士,主要從事計算機應用方面的研究,(E-mail)guangjian224@126.com;

1673-1549(2014)06-0030-04

10.11863/j.suse.2014.06.08

TP242

A