旋轉控制固定鴨舵二維彈道修正彈氣動特性

吳 萍,陳少松,楊晉偉,譚獻忠,杜學偉

(1.南京理工大學 能源與動力工程學院,南京 210094;2.淮海工業集團有限公司,山西 長治 046012)

遠程精確打擊是現代武器裝備發展的方向,導彈是精確打擊武器的代表。導彈可以遠程發射并直接對目標予以毀滅性的打擊,但是它的造價昂貴,無法大規模裝備使用[1]。彈道修正彈通過加裝低成本的修正機構,對原本無控飛行的彈道進行修正,提高彈箭射擊密集度,實現精確打擊。彈道修正彈特別適合于遠程彈箭,通過改進原有引信,加裝修正機構,即可達到對原本無控彈箭進行精確化改進的目的,具有成本低、精度高、性價比高的優點[2]。

彈道修正是在彈箭飛行彈道的合適位置,通過修正機構的作用改變彈箭的氣動外形以改變氣動力,進而對彈箭的飛行彈道進行修正,提高射擊密集度。彈道修正彈分為一維彈道修正彈和二維彈道修正彈。一維彈道修正彈通過增加縱向的氣動阻力來實施對射程的改變,達到提高射擊縱向密集度的目的。早在1994年,美國陸軍裝備研究發展與工程中心(ARDEC)就開始推進基于GPS定位的自動修正阻力器式(一維距離修正式)和制導式(距離和方向二維修正式)引信的研究工作;二維彈道修正彈不僅要改變縱向氣動力,還要改變橫向氣動力,實現對彈箭縱向距離和橫向偏差的修正,提高縱橫向的密集度指標[3]。2003年美國陸軍就提出二維彈道修正引信的采購項目,即XM1156式精確制導組件(PGK)的低成本彈道修正引信采購項目,加裝該二維彈道修正引信的二維修正彈預期要達到圓概率誤差50 m的水平[4]。針對高速旋轉榴彈,有一種二維修正機構采用鴨舵修正機構,該鴨舵偏角固定,如圖1所示,2對舵中一對舵呈俯仰偏航姿態,另一對舵呈差動姿態。俯仰偏航舵修正彈丸縱向距離和橫向偏差;差動舵控制修正機構旋轉,控制俯仰偏航舵所處的位置。該種二維彈道修正彈稱為旋轉控制固定鴨舵二維彈道修正彈。關于這種結構二維彈道修正彈的氣動力研究所見報道很少,文獻[5-6]采用數值模擬的方法對此種類型的全彈氣動力和鴨舵修正氣動力進行了研究。

圖1 XM1156式精確制導組件(PGK)

本文采用風洞實驗研究方法,對該彈在亞跨超音速時不同舵偏角下俯仰氣動特性、滾轉氣動特性、升阻比的氣動特性進行了研究,得到了各氣動參數隨馬赫數、攻角和舵偏角的變化規律,為這種彈的彈道設計和研究提供了參考依據。

1 風洞及實驗模型

本實驗是在某HG-4號風洞中進行的。HG-4號風洞為直流下吹暫沖式閉口高速風洞,實驗段截面為300 mm×300 mm,實驗段長為600 mm。

實際飛行過程中,差動舵差動方向與彈的旋轉方向相反,起到旋轉剎車的作用,最終使得差動舵和俯仰舵組成的修正頭部與彈體隔轉,即該部分相對大地坐標系不轉。當需要進行縱向修正時,俯仰舵處于水平位置,向上或向下打舵使彈增加或縮短射程;當需要進行橫向修正時,俯仰舵處于豎直位置起偏航作用,向左或向右打舵使彈向左或向右偏轉。由于引信部分在修正過程中相對大地坐標系不轉,在本文的實驗中模型的舵偏角也呈固定狀態。

本實驗設計了2種模型,2種模型的外形結構尺寸相同,尖拱形頭部、圓柱形模型身和船尾形模型尾;修正機構有一對俯仰舵和一對差動舵。同一種模型舵偏角度相同,不同種的模型舵偏角度不同,2種模型舵偏角度分別為4°和10°,對應的模型代號為H1和H2,模型外形簡圖如圖2所示。模型外形尺寸滿足亞跨音速的壅塞度和超音速下洞壁反射激波不打在模型上的條件[7]。

圖2 組合體模型簡圖

實驗過程中模型的俯仰舵(偏航舵)處于水平位置,舵朝上偏,零攻角下產生正升力;差動舵處于垂直位置。模型以尾支撐的方式安裝在天平上,天平由風洞中的攻角機構支撐,圖3為模型在風洞實驗段照片。實驗中攻角的變化范圍為:-4°～+8°,馬赫數范圍為0.6～3.930 5。

圖3 模型在風洞實驗段

模型的參考面積選取最大橫截面積S,俯仰力矩系數和壓心系數的參考長度選總長度L、滾轉力矩系數的參考長度選取最大截面對應的直徑D,俯仰力矩系數參考點距模型頭部頂點的相對距離(與模型長度之比)為0.646 7,滾轉力矩系數參考軸取模型對稱軸,壓心系數參考點取彈頂點。實驗模型單位長度的雷諾數見表1。

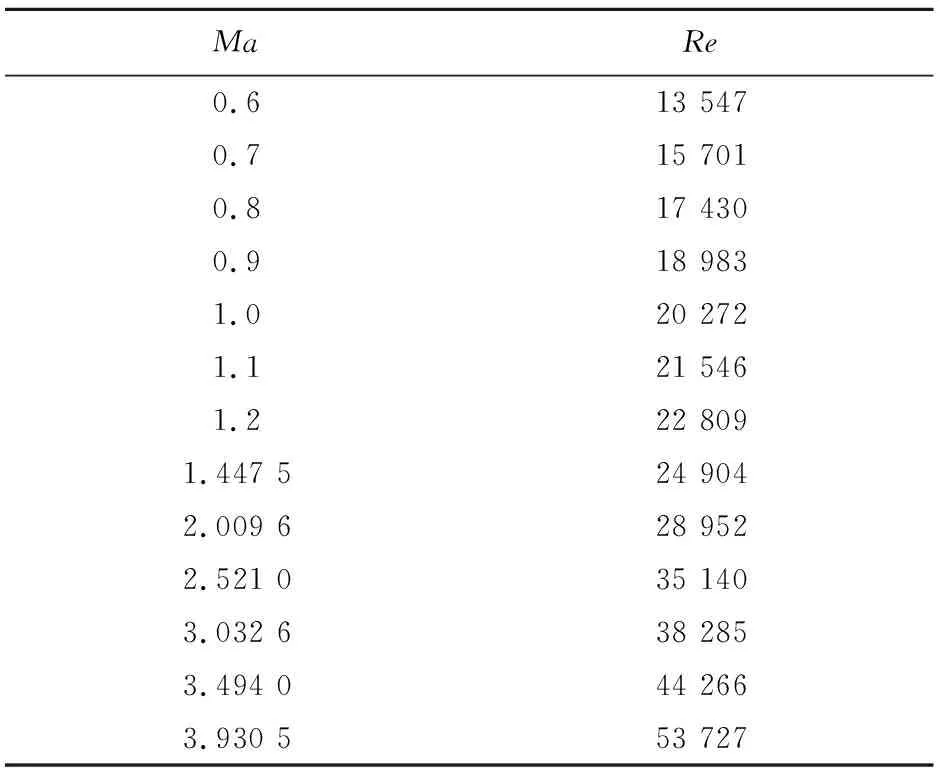
表1 實驗模型單位長度雷諾數

2 實驗結果及分析

2.1 阻力系數

圖4給出了阻力系數CD隨馬赫數變化曲線,由圖4分析發現,H1、H2模型阻力系數CD都是隨馬赫數先增大后減小的,在Ma=1.1時達到最大值。這是由于在跨音速附近彈身已產生激波,使得波阻迅速增大,而動壓增加有限,所以阻力系數增加迅速。在超音速時,隨著速度的繼續增大,激波傾角越來越大,波阻有所降低,而動壓增加明顯,所以阻力系數呈下降趨勢。該變化趨勢符合氣動規律。

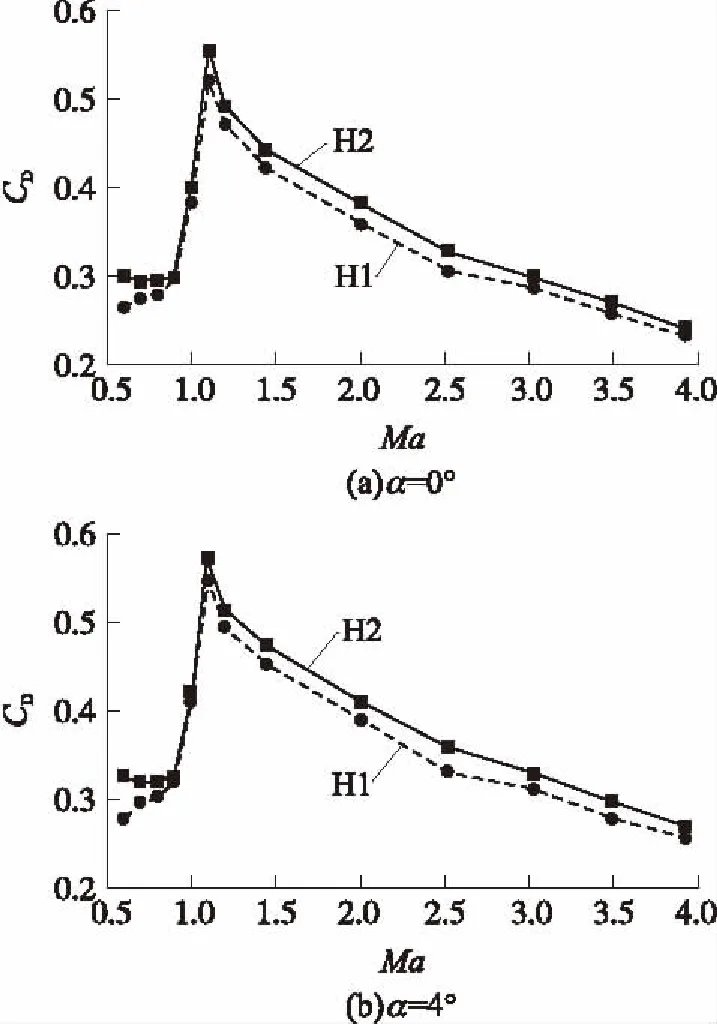
圖4 兩模型阻力系數CD隨Ma變化曲線

圖4顯示H2模型阻力系數大于H1模型,主要是舵偏角增加了迎風的面積,增加了阻力。亞音速時,隨著速度的減小舵偏角增阻情況越明顯,0°攻角時最大增阻率達到12.76%;跨超音速時,舵偏角增阻效果幾乎相同,阻力系數曲線幾乎平行,平均增阻率為4.82%。

圖5為H1模型在馬赫數Ma=2,攻角α=0°拍攝的紋影照片,從圖中可以明顯看到第1道激波出現在模型的頭部,第2道激波出現在舵片前緣處,第3道激波出現在模型頭部圓柱段與模型身部接觸處。第1道激波與第2道激波有一定的交錯,這是因為模型頭部的尖錐半頂角沒有舵片的前緣后掠角的余角大,波后氣流有所減速,使得舵片前緣產生的激波傾角大于模型頭部激波傾角,從而產生交錯。第3道激波主要是由模型頭部圓柱段與模型身部結合處有凹向臺階造成的,超音速氣流受此擾動產生激波。

圖5 H1模型Ma=2,α=0°時紋影照片

2.2 升力系數

在不同馬赫數下,升力系數CL隨攻角α的增加均呈線性增加,圖6給出了Ma=2時升力系數隨攻角變化曲線。由于模型的俯仰舵有一個正舵偏角,此舵偏角使舵片產生升力,所以模型處于0°攻角時總是有個正的升力系數。由于H2模型舵偏角大于H1模型,H2模型的升力系數在實驗攻角范圍內均大于H1模型的升力系數,所以圖6中H2的升力系數曲線一直處于H1的上方。

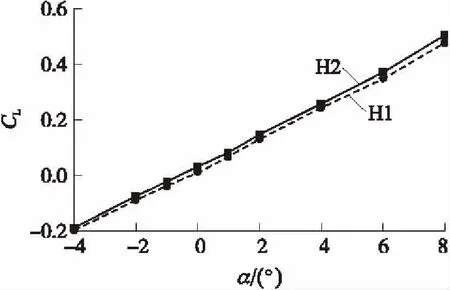
圖6 Ma=2時模型H1、H2的CL隨α變化曲線

模型的差動舵面舵偏角在升力方向的投影面積較小,且產生的升力方向相反,對全彈的升力特性沒有貢獻。

圖7所示為攻角α=8°時升力系數CL隨Ma變化曲線。從圖7中可見,升力系數CL隨Ma變化趨勢基本相同,在亞音速段升力系數先減小后增大,在馬赫數Ma=0.8時達到最小值;在超音速階段CL隨Ma的增大而增大,在Ma=3.0附近達到最大值后隨馬赫數的增大而減小。同一Ma下,H2模型的CL均大于H1模型的CL,說明在實驗范圍內,舵偏角越大,模型的升力系數越大。

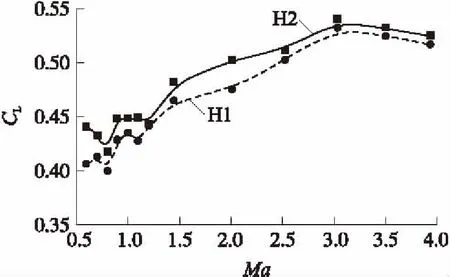
圖7 H1、H2模型CL隨Ma變化曲線

攻角α=0°時,升力系數CL隨舵偏角δ變化曲線如圖8所示。在舵偏角δ=0°,攻角α=0°時,由于模型的對稱性,可以預知模型的升力系數CL=0 。由圖8可以發現,升力系數CL隨著舵偏角δ的增大而增大,僅在個別Ma下呈現線性特性,多數Ma下呈現非線性。

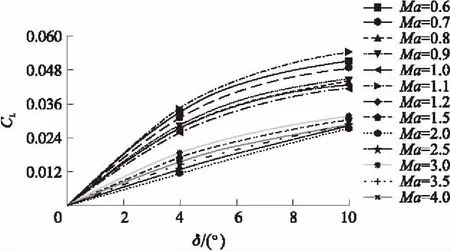
圖8 α=0°時CL隨δ變化曲線

2.3 俯仰力矩系數

圖9給出了攻角α=4°時俯仰力矩系數Cm隨Ma變化曲線,由圖可見,兩模型俯仰力矩系數的變化規律一致。在跨音速階段Cm先波動上升再下降,在Ma=1.2時達到最小值;在超音速段,Ma>1.2后,Cm先上升并在Ma=1.5時達到最大值;Ma>1.5以后,Cm呈下降趨勢。俯仰力矩是彈體法向力對參考點的力矩,它的大小取決于法向力的大小、合力作用點(壓心)相對參考點的位置。模型法向力主要有3個來源:①模型體頭部和靠近頭部的圓柱產生的法向力;②模型體船尾部產生的法向力;③模型俯仰舵產生的法向力。在攻角為正時,模型頭部、圓柱部和俯仰舵產生的法向力為正,且占主導地位,船尾部產生負法向力,其合力的作用點位于力矩參考點之前,所以產生正的俯仰力矩。

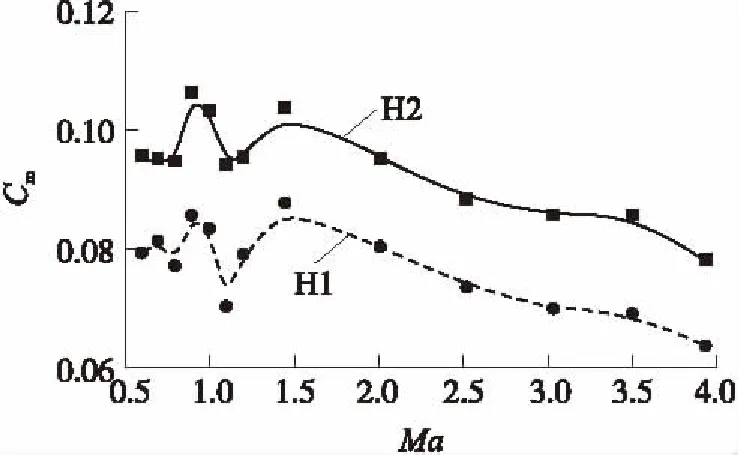
圖9 α=4°時Cm隨Ma變化曲線

在相同Ma、α情況下,模型頭部、靠近頭部的圓柱段及船尾部產生的法向力基本一致;不同的是俯仰舵產生的法向力,舵偏角越大則舵片上下面壓差越大,產生的法向力越大;當俯仰力矩參考點位置相同時,H2模型的俯仰力矩系數Cm總是比H1模型的大。圖10給出了Ma=2的俯仰力矩系數Cm隨攻角α的變化曲線,結果顯示俯仰力矩系數隨攻角的增加呈線性增加,且H2模型的俯仰力矩曲線一直處于H1模型的上方。俯仰力矩系數大說明改變二維修正彈姿態的控制能力大,可以較容易地進行二維修正。

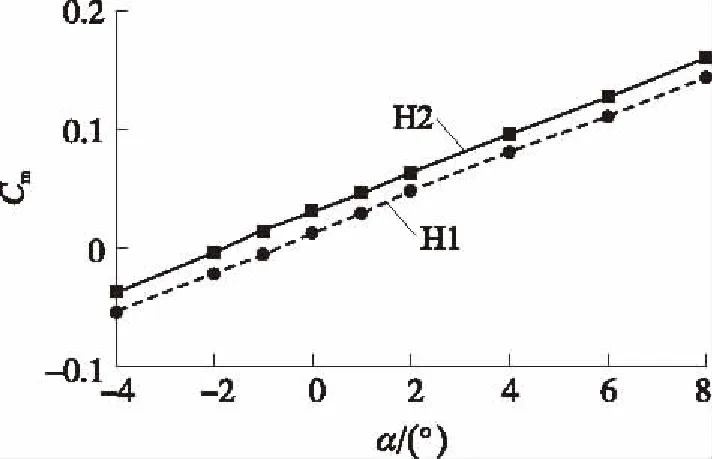
圖10 Ma=2時Cm隨α變化曲線

2.4 滾轉力矩系數

圖11給出了H1、H2模型的滾轉力矩系數Cl隨Ma的變化曲線。在跨音速階段Cl曲線呈波動式下降趨勢,在超音速階段Cl隨馬赫數增加先增大后減小,在Ma=2附近達到最大值。滾轉力矩主要是由處于模型頭部上下位置的差動舵產生,由于一對舵偏角呈差動位置,一片舵片產生的垂直舵面的力與另一片舵面產生的垂直舵面的力方向相反,但對彈軸的力矩方向相同,其合力矩就是滾轉力矩。隨著差動舵偏角的增加,垂直舵面的力增加,滾轉力矩也就增加,所以H2模型產生的滾轉力矩大于H1模型產生的滾轉力矩,滾轉力矩系數大使得控制修正機構旋轉的能力大。

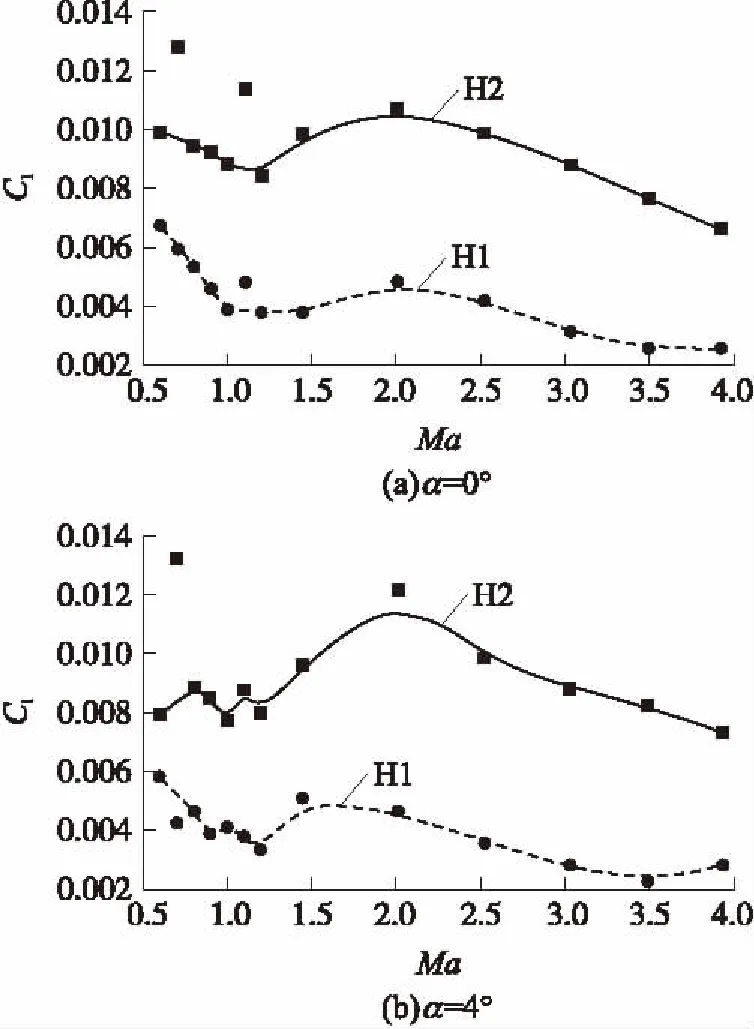
圖11 不同攻角下Cl隨Ma變化曲線

3 結論

旋轉控制固定鴨舵二維彈道修正彈模型風洞實驗研究表明:

①模型阻力系數隨馬赫數變化符合旋轉彈阻力系數變化的氣動規律,舵偏角的增加有一定的增阻效果,H2模型的阻力系數大于H1模型的阻力系數。亞音速下隨著速度減小增阻效果增加,跨超音速下增阻效果幾乎相同。

②在所研究的攻角范圍內,升力系數隨攻角增加呈線性增加,舵偏角的增加使得升力系數增加;0°攻角時,升力系數隨舵偏角增加僅在個別馬赫數下呈線性增加,多數馬赫數下呈現非線性變化特性。

③俯仰力矩系數隨攻角增加呈線性增加,隨著舵偏角的增加而增加。在跨音速階段,俯仰力矩系數先波動上升再下降,在Ma=1.2時達到最低值;Ma>1.2后先上升并在Ma=1.5時達到最大值;Ma>1.5以后呈下降趨勢。

④滾轉力矩系數隨舵偏角的增大而增大;在亞跨音速下隨馬赫數增加而減小,Ma=1.1時達到最小值,當馬赫數增加至2.0時達到最大值,以后隨馬赫數增加而減小。

[1] 張民權,劉東方,王冬梅,等.彈道修正彈發展綜述[J].兵工學報,2010,31(12):127-130.

ZHANG Min-quan,LIU Dong-fang,WANG Dong-mei,et al.A summary for trajectory correction projectiles[J].Acta Armamentarii,2010,31(12):127-130.(in Chinese)

[2] 楊慧娟,霍鵬飛,黃崢.彈道修正彈修正執行機構綜述[J].四川兵工學報,2011,32(1):7-9.

YANG Hui-juan,HUO Peng-fei,HUANG Zheng.Overview of correction executive mechanism on trajectory correction projectile[J].Journal of Sichuan Ordnance,2011,32(1):7-9.(in Chinese)

[3] 馬寶華.戰爭、技術與引信——關于引信及引信技術的發展[J].探測與控制學報,2001,23(1):1-6.

MA Bao-hua.War,technology and fuze—about fuze and fuze technology development[J].Journal of Detection & Control,2001,23(1):1-6.(in Chinese)

[4] 華菊仙.彈道修正引信讓笨彈變聰明[J].現代兵器,2006(8):13-16.

HUA Ju-xian.Trajectory correction fuze make bullet smarter[J].Modern Weaponry,2006(8):13-16.(in Chinese)

[5] 郝永平,孟慶宇,張嘉易.固定翼二維彈道修正彈氣動特性分析[J].彈箭與制導學報,2012,32(3):171-173.

HAO Yong-ping,MENG Qing-yu,ZHANG Jia-yi.Aerodynamic characteristic ananlysison two-dimensional trajectory corrector shell with fixed-wing[J].Journal of Projectiles,Rockets,Missiles and Guidance,2012,32(3):171-173.(in Chinese)

[6] 張嘉易,王廣,郝永平.二維彈道修正彈鴨舵修正機構氣動特性研究[J].彈箭與制導學報,2013,33(2):121-124.

ZHANG Jia-yi,WANG Guang,HAO Yong-ping.The investigation of aerodynamic characteristics for two-dimensional trajectory correction projectile canard rudder device[J].Journal of Projectiles,Rockets,Missiles and Guidance,2013,33(2):121-124.(in Chinese)

[7] 王鐵城.空氣動力學實驗技術[M].北京:國防工業出版社,1986.

WANG Tie-cheng.Aerodynamic experiment technology[M].Beijing:National Defence of Industry Press,1986.(in Chinese)