炮彈三維密集度指標體系研究
盧國勝,郭尚生
(1.中國人民解放軍駐七二四廠軍事代表室,沈陽 110045;2.遼沈工業集團有限公司,沈陽 110045)
目前,炮彈密集度指標都是以二維坐標給定和檢查,對于地面壓制性作戰,火炮可以基本滿足論證研制、生產制造、檢驗驗收和作戰指揮的需求,但對在空中引爆開艙的照明彈、偵察彈和對空中目標作戰的榴彈,以及用時間引信空中引爆后對地面目標作用的炮彈,用二維坐標考核密集度就顯得不準確、不直觀和不方便。為了解決目前炮彈密集度指標都以二維坐標給出并考核的不足,通過對目標特性進行剖析,對各類炮彈終點效應進行分析,在概率論的基礎上,本文研究建立三維密集度指標體系的理論基礎和考核方法,為炮彈在論證、制造、檢驗和作戰指揮中快速、精確使用密集度指標提供了理論基礎。
三維密集度指標體系可以解決二維密集度指標體系的不足,同時,由于計算機技術的成熟應用,三維指標體系可以更精確、更快速完成射擊諸元的指揮、裝定和修正。
1 三維密集度指標體系的建立
炸點密集度散布一般服從正態分布,在各個方向上互不相關,可由n維分布規律進行推導[1-2]。
相互獨立的三維正態分布的邊際密度為
式中:σm為各維的散布方差,μm為各維的散布中心,xm為各維的落點,下標m代表x,y,z。
相互獨立的三維正態分布的聯合密度為
f(x,y,z)=f1(x)f2(y)f3(z)=
則有相互獨立的三維正態分布的聯合分布函數為
F(-a1 (3) 相互獨立的三維正態分布的概率分布由其聯合分布函數確定[3],即: P{-a1 (4) 炮彈在空中引爆,一是直接對空作戰,如毀傷飛機、導彈、投放物;二是在空中引爆后作用于地面目標,如實施照明、發煙,以及子母彈子彈對地面目標作用、未敏彈子彈對地面目標作用等。后者對目標作用可借用普通炮彈的二維密集度形式,但需要考慮等效計算的算法和精確度;前者對目標作用的炸點散布,需要進一步對其作用要求和考核方法進行研究。首先,要確定目標空間大小,找到炮彈對目標作用可靠性的分布規律;其次,要明確作戰時對目標的命中概率要求,據此計算出彈丸在空中炸點散布密集度的指標要求。 例,某榴彈需要用于打擊3 000~5 000 m處,幾十m至數百m高度的武裝直升機目標。假設目標為矩形立方體,如圖1所示,并且射彈的空中炸點為三維球形散布,服從正態分布,并各自獨立,則可由式(3)、式(4)推出命中目標的概率: 式中:a,b,c分別為立方體目標的長、高、寬;Ex為發射系統的縱向中間誤差值;Ey為發射系統的高度中間誤差值;Ez為發射系統的橫向中間誤差值;Φ為標準正態分布函數。 圖1 空中目標示意圖 當a,b,c比較接近時,可以用以下公式近似計算: 式中:P為命中目標的概率,Φ-1為Φ的反函數。 當a=24 m,b=20 m,c=20 m,Em與P的關系如表1所示。 表1 計算實例得到的Em與P的關系 炮彈戰技指標E0與瞄手誤差Er(瞄手誤差值包括除炮彈本身造成的誤差以外的系統誤差)的關系為[1] 若取瞄手誤差Er=0.6 m(按2密位計算),命中概率P=0.9,則該彈在3 000 m處的三維密集度指標應是:Ex0=6.56 m,Ey0=5.46 m,Ez0=5.46 m。 用單臺測量儀器進行單點測量,一次記錄3項數據,分別是測點與炸點的距離Li,炸點相對測點方向角αi,炸點相對測點高低角βi。 事先確定測點坐標A(xA,yA,zA),則測點坐標可由以下公式計算: xi=Licosβisinαi+xA (10) yi=Lisinβi+yA (11) zi=Licosβicosαi+zA (12) 式中:xi,yi,zi為一組試驗數據中第i發的三維落點坐標值。 用2臺測量儀器進行兩點測量,如圖2所示,A、B兩點為儀器測量點,P點為炮彈炸點。一次記錄4項數據,分別是第1測點方向角αAi,第2測點方向角αBi,第1測點高低角βAi,第2測點高低角βBi。 圖2 炸點三坐標示意圖 先確定第1測點坐標A(xA,yA,zA)和第2測點坐標B(xB,yB,zB),并使yB=yA,zB=zA,則所測炸點坐標為 對于炮彈裝備產品建立三維密集度指標體系在理論和實踐上都是可行的,也是必要的。本文建立的三維密集度指標體系可以解決二維密集度指標體系的不足,同時包容各類炮彈滿足論證、設計、考核和使用的要求。通過三維密集度指標體系的建模,可以充分應用計算機技術,使密集度指標體系可以更精確、更快速完成各類炮彈的射擊諸元的指揮、裝定和修正,提高戰術技術指標的實用性。 [1] 姚平中,韓之俊.概率與統計[M].南京:華東工程學院,1983. YAO Ping-zhong,HAN Zhi-jun.Probability and statistics[M].Nanjing:Huadong Engineering College,1983.(in Chinese) [2] 德沃爾 J L.概率與統計(理工類)[M].北京:機械工業出版社,2005. DEVORE J L.Probability and statistics for engineering and the sciences[M].Beijing:China Machine Press,2005.(in Chinese) [3] 馬振華.概率統計與隨機過程[M].北京:清華大學出版社,2005. MA Zhen-hua.Probability and statistics and stochastic process[M].Beijing:Tsinghua University Press,2005.(in Chinese)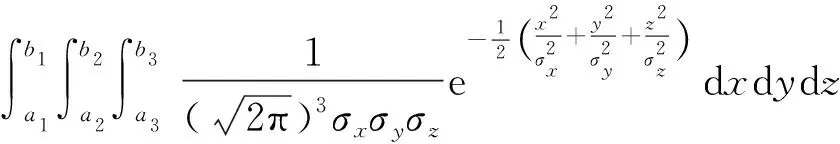
F(az,bx,by)]+[F(ax,ay,bz)+F(ax,az,by)+
F(ay,az,bz)]-F(ax,ay,az)2 空中目標密集度要求的分析
2.1 目標命中要求

2.2 計算實例

3 三維密集度指標的考核
3.1 單點測量三坐標
3.2 兩點測量三坐標

4 結束語

