陀螺外框擺動角受限時某末制導炮彈的彈道特性

佟德飛,宋衛東,劉炳辰

(1.軍械工程學院 火炮工程系,石家莊 050003;2.66294部隊 北京 100042)

在慣性飛行階段,末制導炮彈通過調整舵片的偏轉來實現以基本不變的彈道傾角飛行,從而延長飛行距離[1]。該型末制導炮彈慣導陀螺儀為框架陀螺儀,陀螺轉子沿著彈體縱軸安裝。由于彈體的旋轉,陀螺內框軸和外框軸隨彈體一起旋轉以保證轉子的空間定軸特性,彈體每旋轉一周,陀螺內框以及外框相對彈體交替擺動一次。外框軸擺動信號經處理實現控制信號輸出并對鴨舵實施控制,實現飛行過程中對重力的補償,即為慣導滑行增程的基本原理。

文獻[2]通過仿真實驗分析了基于慣導滑翔增程技術的炮彈彈道特性,不考慮陀螺結構因素影響,內、外框架的擺動不受角度限制,實際上受結構影響,內、外框擺動角度上限為48°。因此,本文分析當外框擺動幅度超過該限定值后轉子定軸性發生的變化,并分析由此改變的飛行控制過程對末制導炮彈彈道特性的影響。

1 慣導陀螺系統的空間運動

1.1 內、外框架擺動運動規律

內、外框架偏轉角度的計算方法仍通過幾何關系的轉換求解,求解關系式為[3]

L(θg,ψg)=L(γg)L(γ)L(φ,ψ)LT(γgd,θgd,ψgd)

(1)

式中:θg,ψg分別為外框、內框擺動角;γg為慣導陀螺相對彈體的安裝角;γ,φ,ψ為末制導炮彈彈體姿態角;γgd為陀螺內框架相對慣性坐標系的偏轉角;θgd,ψgd分別為陀螺轉子相對慣性坐標系在鉛垂面上及水平面上的偏轉角。根據慣導陀螺結構特點,給定|θg|>48°為轉子內、外框架的碰撞條件。

1.2 轉子進動計算模型

目前,轉子碰撞相關問題的研究對象多為汽輪機轉子等大型機械,主要分析轉子與周圍機械部件存在摩擦碰撞情況下的動力學行為[4-6]。對于慣導陀螺儀擺角受限,外框的碰撞問題很少有文獻提及。

根據轉子歐拉運動方程,轉子受到外力矩后的運動方程為

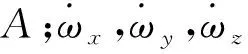
式中:ω1為受沖擊力矩作用之前轉子的轉動角速度,并假設其保持恒定值。因此轉子轉過的角度可表示為

dr=ωxdt

(4)

將式(2)中后2個公式化為容易積分的線性方程式,將角速度化為以r為變量,即

因此可得:

將my,mz同樣轉換為以r為變量,引入復數量:

ωy+iωz=ω,my+imz=m

(7)

將方程(6)化為下列形式:

ω′+ipω=m

(8)

因此,式(8)的解形式為

(9)

由此,作用在轉子上的力矩不同就會使其產生不同的運動。

2 轉子進動分析

由于無法通過實驗確定轉子的外框架受限后轉子的運動,本文從理論上對轉子可能產生的運動分為3種情況進行研究:

①外框架擺角超限后起到限位作用。轉子完全失去繞外框轉動的自由度,轉子隨彈體進動,進動角速度方向同彈體轉動角速度方向。

②外框架擺角超限后,內、外框架發生不完全彈性碰撞。通過給定碰撞沖量,分析轉子受到恒定外力矩作用下的進動運動。

③外框架擺角超限后,內、外框架完全彈性碰撞,轉子受到沖擊力矩的作用。

2.1 限位條件下的轉子進動

限位作用使陀螺系統失去一個自由度,陀螺儀變成二自由度陀螺。當彈體繞陀螺儀缺少自由度的方向轉動時,將強迫陀螺儀隨彈體一同轉動,轉子軸轉動趨向與彈體轉動角速度的方向重合。

2.2 常值激勵力矩作用下的轉子進動

由于轉子固連于內框架,外框架受限后,激勵力矩最后傳遞并作用于轉子。

1)力矩向量垂直于轉子對稱軸。

當外框架超限后,常值激勵力矩垂直于轉子對稱軸時,mx=0,ωx=ω1。轉子在自轉方向上的轉動速度不變。式(2)可解耦,得轉子在另外2個方向上的運動情況。解的形式為

以時間為變量的解為

2)任意方向的力矩向量。

式(2)解的形式為

相對上一種情況,轉子運動還與激勵作用的時間平方相關。

2.3 沖擊作用力矩下的轉子進動

首先假設框架擺動角度受限后存在連續碰撞的可能,用狄拉克函數δ(t)表示沖擊碰撞力矩,即

式中:tν是第ν次沖擊的時間,Mν是沖擊力矩的模值。于是方程的解為

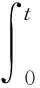
(15)

由于單位階躍函數為

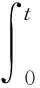
(16)

對該一階線性方程進行求解,并再將時間作為變量得到:

將上述通解進行分解就可以得到轉子在另外2個軸即y,z方向的角速度的值。當內、外框架擺動滿足碰撞條件時,在彈體一個旋轉周期內碰撞可能存在4種形式,分別為內框、外框超限情況下的正向碰撞和逆向碰撞。因此,本文給定判定方案如表1所示。

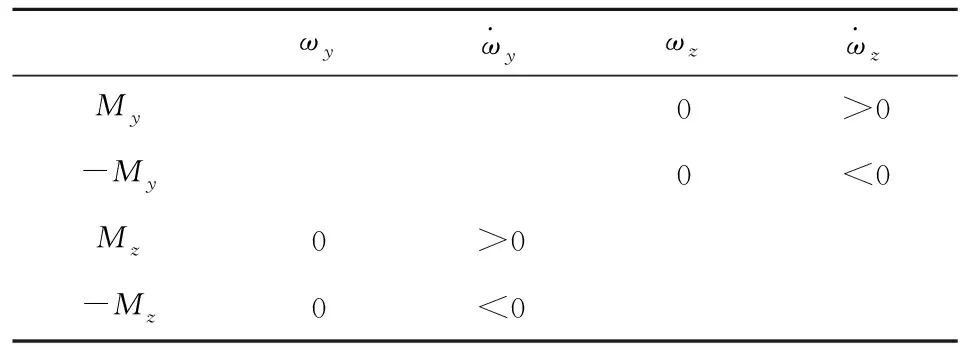
表1 碰撞正向、逆向判定

轉子受到連續沖擊力矩的作用后,每次沖擊都會導致角速度的瞬時值發生階躍變化,因此轉子的運動為不同沖擊引起轉子錐形轉動運動的疊加。

3 轉子運動數值仿真

利用末制導炮彈彈道模型以及慣導控制模型[2],建立彈道數值仿真系統,給定慣導陀螺啟動時間為12.4 s。

按照轉子運動的第①種情況,當轉子外框擺動角超限后起到限位作用,將三自由度慣導陀螺強制變為二自由度陀螺,轉子隨彈體向下進動,并在下一次外框擺角受限之前保持該偏轉角度不變。在彈道降弧段,彈體向下偏轉角速度約為1.5(°)/s。轉子在空間中的角度變化如圖1所示。

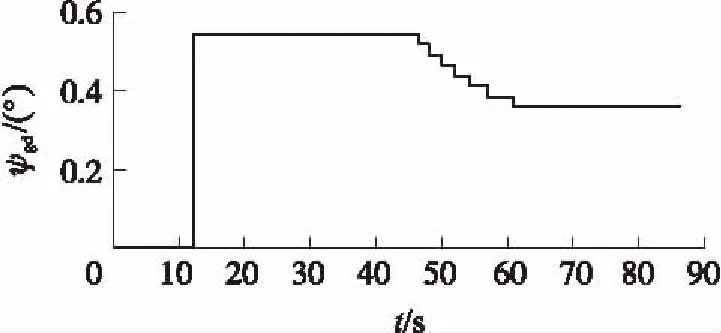
圖1 限位條件下的轉子偏轉角度

按照限位條件進行計算時,轉子在縱向平面內向下偏轉,隨載體向下進動,進動約0.183 rad。按照轉子運動的第②種情況,轉子將同時繞內、外框軸偏轉;如圖2所示。

按照恒值力矩條件進行計算時,轉子在水平面以及縱向平面偏轉相同的角度,但變化過程比較平緩,轉子分別轉過-0.19 rad。恒值力矩激勵作用下的轉子運動是錐形運動。按照轉子運動的第③種情況,轉子轉動角速度受到沖擊激勵力矩作用的影響。給定外框架碰撞時刻相互作用力矩,并在0.005 N·m～0.02 N·m之間取值。轉子空間偏轉角速度變化情況如圖3所示。

圖2 恒值力矩條件下轉子偏轉角度

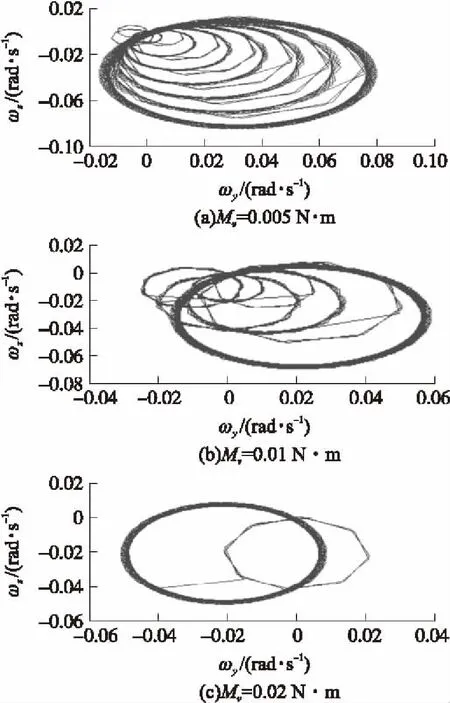
圖3 不同沖擊力矩時的轉子擺動角速度

轉子受到力矩作用后在空間發生錐形運動,每次碰撞都使轉子偏轉半徑或角度不斷增大。對上述轉子空間偏轉角速度進行積分,就得到轉子偏離原轉動軸的偏轉角度。積分結果如圖4所示。

按照沖擊力矩激勵條件進行計算時,轉子在空間擺動運動復雜,由于轉子的空間運動由錐形運動進行疊加,對其進行積分就得到轉子在空間的偏轉情況。當給定沖擊力矩為0.02 N·m時,轉子向下以及向右偏轉-0.77 rad;當給定沖擊力矩為0.01 N·m時,轉子向下以及向左偏轉分別約為-1.3 rad,0.65 rad;當給定沖擊力矩為0.005 N·m時,轉子向下以及向左偏轉分別約為-1.2 rad,1.1 rad。

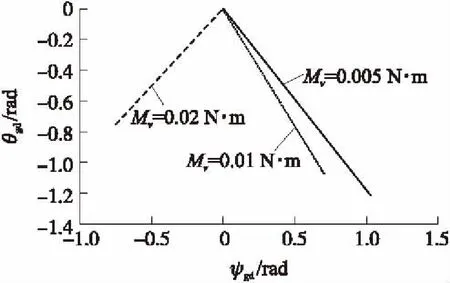
圖4 沖擊力矩條件下轉子空間偏轉角度

轉子定向性的變化對末制導炮彈的彈道特性產生了很大的影響。

4 外框擺動角超限對彈道特性的影響

根據末制導炮彈彈道方程,對末制導炮彈彈道特性進行數值仿真。當外框擺動角超過限制后,轉子空間定軸性受限受到影響,進而對控制過程的計算基準產生計算誤差。

外框擺動角不受限制條件下,圖5(a)為整個飛行過程中外框架擺動角的變化規律,圖5(b)為圖5(a)局部視圖。

圖5 不受限條件下外框擺動規律及局部擺動視圖

考慮實際情況,當轉子外框受到限制時,按限位條件計算,轉子失去一個自由度,于是轉子軸隨載體進動。由于每次改變轉子角度并不大,轉子軸與彈軸夾角的減小并不能保證在第一次外框擺角超限后不再超過該限制。限位條件下,飛行過程中的外框擺動角如圖6所示。

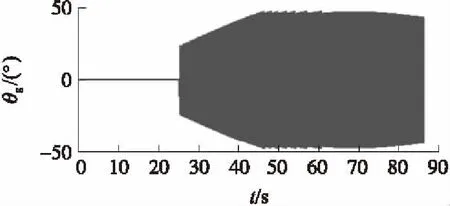
圖6 限位條件下外框擺動規律

轉子受到恒值力矩條件下,每次轉子偏轉角度較小,外框架擺動規律如圖7所示。

圖7 恒值力矩條件下外框擺動規律

圖8為外框擺動角受限后轉子受到不同沖擊力矩條件下外框架的擺動規律。3種工況都使轉子軸與彈軸夾角不斷減小。

圖8 不同沖擊力矩條件下外框擺動規律

根據數值計算,外框擺動過程按照不同計算方式差異比較明顯,并且造成的彈道特性差距也很大,具體給定的數值如表2所示。

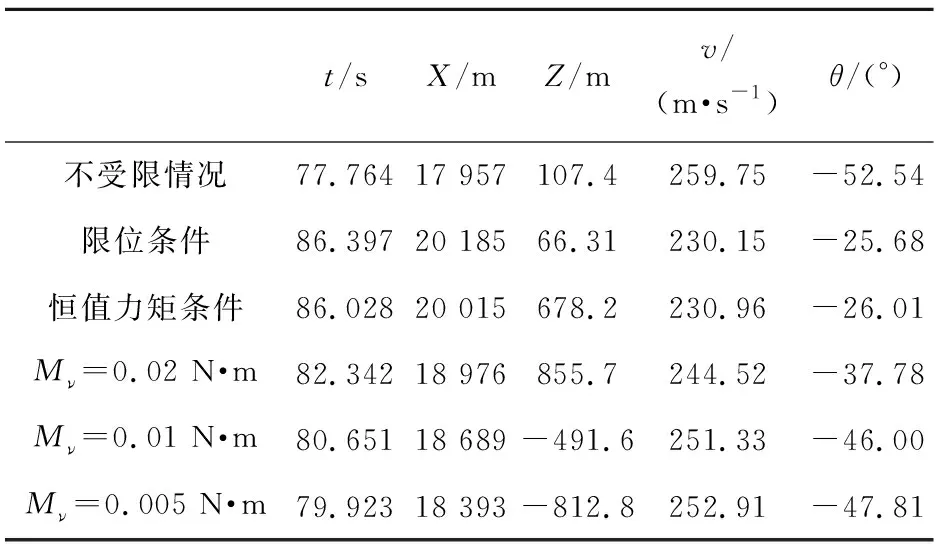
表2 不同結構條件下名義彈道落點諸元

不受結構限制條件下,通過仿真計算,外框擺動角也超過-55°～55°的擺角測量范圍,因此對控制信號作不輸出處理。因此,落角增大,并且未保持在慣導滑行階段以-26°左右傾角飛行,這證明慣導滑行階段控制舵片偏轉并未起到重力補償的作用。

從表中可以看出,按照限位條件以及恒值力矩條件計算時,轉子空間角度的變化并不劇烈,同時在控制彈體慣性滑行階段,能夠保證其彈道傾角緩慢變化,減小飛行落角。飛行距離較不受限條件分別增加約2 228 m,2 058 m,側偏變化約-41.9 m,570.8 m。

按照沖擊力矩計算時,轉子空間擺動變化較大,每次結構上的限制都使轉子軸與彈軸夾角減小,使其控制過程發生如圖8所示的變化規律。通過給定單次碰撞所產生的沖擊力矩計算得到,當沖擊力矩越小時,最終落點單元的落角越大且造成的轉子空間偏轉角度也大。最終落角都要比-26°大得多,也說明了舵片參與重力補償的不充分。與不受限情況進行比較時,彈道性能在射程、側偏等因素方面差距較大。飛行距離較不受限條件分別增加約1 019 m,732 m,436 m,側偏變化約748.3 m,-599 m,-920.2 m。

根據數據比較,可以得出結論:①當轉子外框擺動角受結構限制而僅起限位作用時,轉子隨載體進動。由于載體偏轉變化平緩,慣導控制過程能夠較為準確地提供重力補償,使彈體能夠慣性滑行,延長飛行距離。②當轉子外框擺動角受限后,受到沖力矩的作用而進動時,外框擺動角受限最終的結果就是轉子圓錐運動的疊加。計算表明轉子運動變化較為劇烈,控制過程變化未能使彈體慣性滑行段提供有效的重力補償,飛行距離有一定的變化,但造成的側偏很大。

5 結論

本文從理論上分析了末制導炮彈慣導陀螺外框架擺動受限后,其可能造成轉子發生的3種運動。采用歐拉運動學方程建立了轉子運動計算模型,分析了轉子在限位條件、恒值激勵力矩、不同沖擊力矩作用下轉子的進動運動。結合末制導炮彈外彈道模型并進行了數值仿真,分別研究了外框擺動角受限后3種轉子進動模型對彈道特性造成的影響。限位條件下,轉子跟隨彈體運動,對彈道性能影響不大;恒值力矩激勵條件下,力矩越大,對彈道影響越大;沖擊力矩作用下,轉子空間運動為錐形運動的疊加,對彈道性能影響很大。本文為深入分析末制導炮彈在極限運動條件下的彈道特性提供了理論基礎。

[1] 宋衛東,張進忠.慣導陀螺零漂對末制導炮彈彈道性能的影響[J].南京理工大學學報,2010,34(2):162-163.

SONG Wei-dong,ZHANG Jin-zhong.Influence of zero drift of inertial guide gyro on trajectory characteristics of terminal guide shell[J].Journal of Nanjing University of Science and Technology,2010,34(2):162-163.(in Chinese)

[2] 趙慶嵐.激光末制導炮彈彈道特性及射表編擬方法研究[D].石家莊:軍械工程學院,2008.

ZHAO Qing-lan.Research on ballistic performance and method of making firetable of laser terminal guidance projectile[D].Shijiazhuang:Ordnance Engineering College,2008.(in Chinese)

[3] 劉炳辰.基于多剛體理論的某型末制導炮彈彈道建模與仿真[D].石家莊:軍械工程學院,2011.

LIU Bing-chen.Modeling and simulation of terminal guide projectile trajectory based on multi-body dynamics theory[D].Shijiazhuang:Ordnance Engineering College,2011.(in Chinese)

[4] 孫政策,徐建學,周桐.高速碰摩轉子的復雜動力學行為分析[J].機械科學與技術,2002,12(6):923-928.

SUN Zheng-ce,XU Jian-xue,ZHOU Tong.Analysis of the complicated characteristics of a high-speed rotor system with rub-impact[J].Mechanical Science and Technology,2002,12(6):923-928.(in Chinese)

[5] 王秉仁,劉兆陽.基于非線性理論的碰摩轉子動力學特性研究[J].汽輪機技術,2006,48(6):422-426.

WANG Bing-ren,LIU Zhao-yang.Research on dynamic character of rub-impact based on nonlinear theory [J].Turbine Technology,2006,48(6):422-426.(in Chinese)

[6] 王濤,傅行軍.基于Hertz接觸模型的碰摩轉子動力學響應研究[J].汽輪機技術,2009,51(1):39-42.

WANG Tao,FU Xing-jun.Dynamic response of rub-impact rotor based on Hertz contact model [J].Turbine Technology,2009,51(1):39-42.(in Chinese)

[7] 佟德飛,宋衛東,賈波.陀螺轉子質量偏心對末制導炮彈彈道特性的影響[J].彈道學報,2014,26(1):26-31.

TONG De-fei,SONG Wei-dong,Jia Bo.Influence of gyroscope rotor mass eccentricity on ballistic of terminal guided projectile[J].Journal of Ballistic,2014,26(1):26-31.(in Chinese)