K裝藥桿式射流形成及侵徹研究

周 歡,李偉兵,李文彬,陳 闖,吳 巍

(1.南京理工大學 智能彈藥技術國防重點學科實驗室,南京 210094;2.63863部隊,吉林 白城 137001)

隨著現代裝甲防護技術的發展,特別是伴隨著復合裝甲(rolled homogenous armor)的出現,傳統的成型裝藥結構已無法滿足戰場需求。K裝藥作為一種高效、低長徑比的射流裝藥,以其形成的射流速度和形成率高、杵體小且分散、侵徹能力強而聞名[1]。早在20世紀90年代,國外Chanteret P Y、Mattsson K、Sorensen J[2-3]等人就對K裝藥結構中隔板參數、裝藥長徑比、藥型罩材料等因素對射流成型與侵徹能力的影響做過較為系統的試驗研究,得出K裝藥較傳統裝藥具有裝藥量小、成型好、侵徹威力強等優點。后來Funston R J[4]等人設計出一種新型K裝藥結構,其可形成高速連續的桿式射流,侵徹威力可進一步提高。國內張先鋒、王樹有、黃正祥、黃風雷[5-8]等人也對K裝藥成型及射流侵徹金屬靶板方面進行過大量的仿真和試驗研究并取得了較大進展。但裝藥中隔板的存在使得作用在藥型罩上的爆轟載荷變得復雜,其形成特殊的射流類型、成型機理是否與傳統射流形成模型一致,與同等裝藥及藥型罩結構形成的射流具體存在哪些優勢,這些問題都有待研究。

本文針對K裝藥結構,基于改進的射流成型理論與相關試驗擬合公式,通過Mathematica數學軟件編程來計算分析射流成型過程,并利用Autodyn數值仿真軟件對其進行驗證,定量比較了傳統錐形罩裝藥與K裝藥射流形成情況。最后,優化設計出適用于K裝藥的偏心亞半球型藥型罩,并進行靜爆試驗驗證。

1 K裝藥射流形成的理論模型

1.1 理論模型假設

本文引用考慮微元壓垮加速過程的適用于任意藥型罩形狀和任意起爆方式的一般射流分析理論[9],并對該理論作如下假設:

①裝藥結構為軸對稱結構;

②罩微元在壓垮期間藥型罩單元之間無相互作用且微元沿軸向匯聚之后做軸向平動;

③罩微元的極限壓垮速度僅與其對應的軸向裝藥質量和徑向裝藥質量有關;

④罩微元壓垮過程是一個指數形式的加速過程;

⑤不考慮射流的斷裂情況。

1.2 射流形成的計算分析

藥型罩壓垮過程如圖1所示,圖中,α為藥型罩半錐角,λ為爆轟波在微元處法線與藥型罩的切線夾角,vd為炸藥的爆速,任取藥型罩初始時刻P,P′,Q三點位置,經過一段時間后對應位置為J,M,Q,其壓垮過程中涉及到的參數主要包括極限壓垮速度v0(x)、壓垮速度vt(x,t)、飛散角δ(x,t)、壓垮角β(x,t)、射流頭部速度vj(x,t)等,下面簡要介紹文中各參數求解方法。

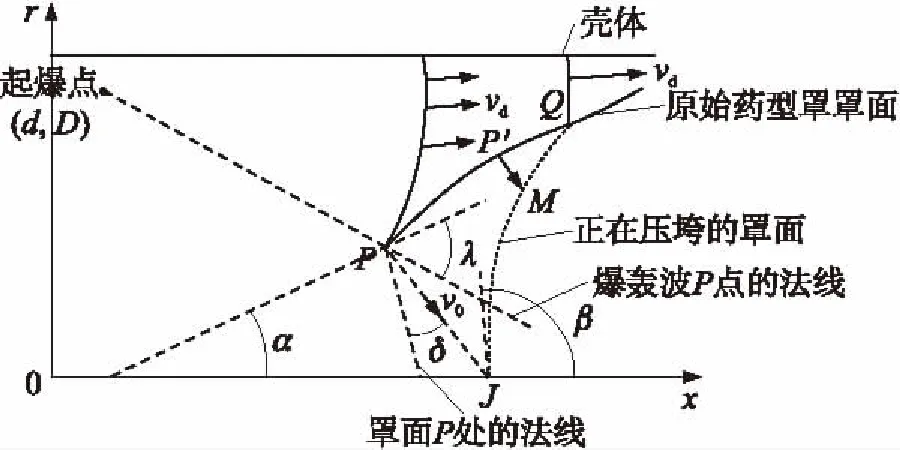
圖1 藥型罩壓垮過程示意圖

對于不帶隔板成型裝藥的單點起爆,一般采用瞬時爆轟假設并不考慮起爆位置。為了計算爆轟波與藥型罩微元接觸時賦予給后者的速度,本文引用較常用的Gurney方法來計算藥型罩的極限壓垮速度v0(x)。

對于文中研究的帶隔板的K裝藥,裝藥通過單點起爆形成發散形爆轟波,然后繞過隔板變成具有環圈陣面的匯聚形環形波,從而增大作用在藥型罩上的爆轟壓力。但對于環形爆轟波的作用,Gurney方法無法反映起爆點變化對壓垮速度的影響。因此,采用德佛紐克斯經驗方程[10]計算極限拋射角,進而通過聯立周培基公式得到極限壓垮速度[11]:

式中:φ0,k0為常數;δ0(x)為罩微元初始飛散角;e(x)(涉及隔板參數)為垂直于微元方向的裝藥厚;ε(x)為藥型罩微元厚度;ρ為藥型罩密度;τ為時間常數。

對于壓垮速度的求解,本文引用蘭德-皮爾森提出的指數型加速公式,式中時間常數τ的求解公式為[12]

式中:E0,γ分別為炸藥狀態參數;m為藥型罩單位面積質量;I為罩微元的比沖量;a1,a2,a3為常數,可通過實驗獲得。

對于飛散角δ(x,t)的計算,本文結合相關文獻[13]中的方法,通過壓垮速度公式類比出飛散角公式:

式中:t0為爆轟波開始到達微元的時間。

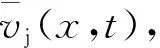
1.3 射流侵徹的計算

文中引用小炸高條件下的連續射流侵徹的計算公式[12],其計算出的侵徹深度在小炸高條件下具有較好的一致性,其式為

2 模型計算及分析

為了比較傳統錐形罩裝藥與K裝藥,下面對同結構錐形罩傳統裝藥與K裝藥的射流成型過程進行計算。其中,裝藥為8701,密度為1.69 g/cm3,爆速為8 425 m/s,2種裝藥結構的裝藥尺寸相同,即裝藥口徑Dk=110 mm,裝藥高度H=125 mm;藥型罩材料均為紫銅,密度為8.96 g/cm3,錐角為36.4°,壁厚為2.2 mm。另外,所選隔板材料為酚醛樹脂,密度為1.2 g/cm3。傳統錐形罩裝藥與K裝藥的結構如圖2所示。

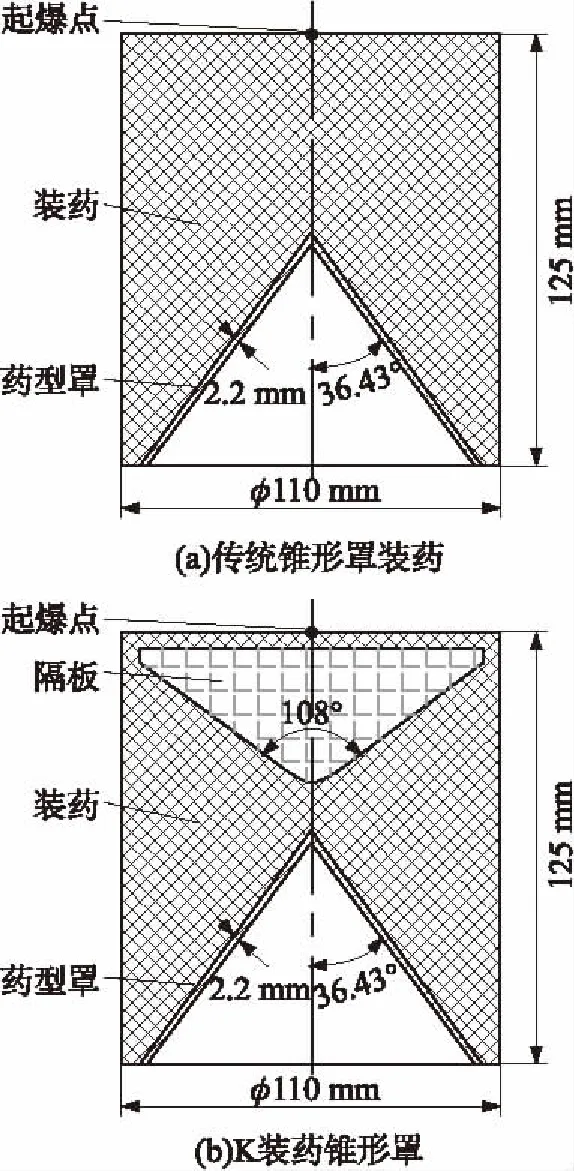
圖2 2種裝藥結構對比

文中利用Mathematica數學軟件編程和Autodyn數值仿真軟件來計算射流成型過程。射流成型仿真時,由于射流成型對單元網格尺寸劃分大小的敏感性較大,因此文中參照相關文獻研究[15]對其進行仿真。

通過給定時刻理論編程計算和數值仿真計算的射流成型情況來驗證理論編寫的射流成型程序是否合理。一般射流在60 μs時刻左右就已經達到全部壓垮狀態,因此下面選取60 μs時刻傳統錐形罩裝藥與K裝藥的射流成型圖進行對比,如圖3所示。可以看出理論計算結果與仿真計算結果大致相同。

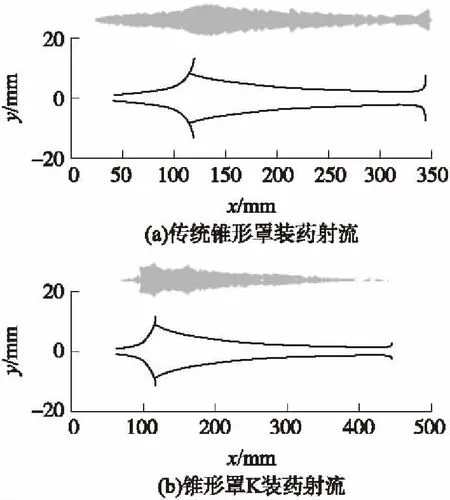
圖3 射流成型理論與仿真計算結果對比(60 μs)

同時,通過計算與仿真獲得了傳統錐形罩裝藥與K裝藥射流成型參數,表1為理論計算結果與仿真結果的對比。傳統錐形罩裝藥仿真與理論計算結果中射流長度l誤差為2.6%、射流頭部半徑r1誤差為3.1%,射流尾部半徑r2誤差為4.8%;K裝藥仿真與理論計算結果中射流長度l誤差為6.4%、射流頭部半徑r1誤差為17%,射流尾部半徑r2誤差為6.5%。K裝藥由于不是最優藥型罩結構,射流形成過程中頭部發生斷裂,而射流形成理論未考慮射流斷裂的影響,因此K裝藥形成射流頭部半徑偏差較大。

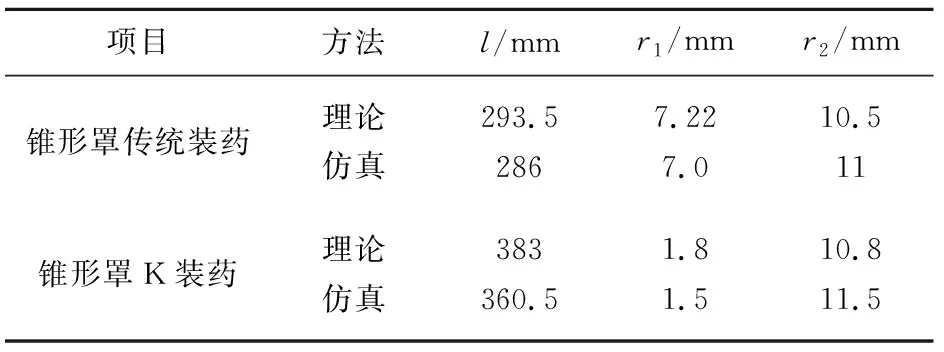
表1 傳統錐形罩裝藥與K裝藥射流成型參數

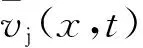
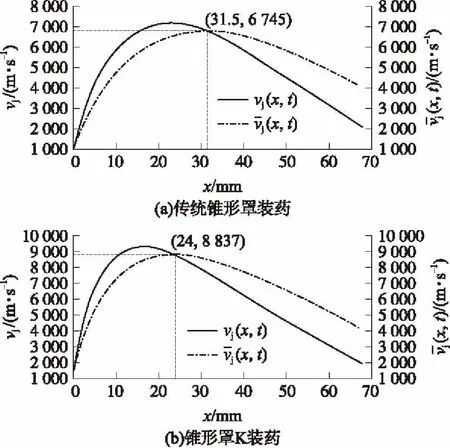
圖4 射流成型頭部速度理論計算結果對比(60 μs)

通過以上2種裝藥相關參數計算與成型對比可知,K裝藥形成射流的頭部速度比傳統錐形罩裝藥提高了31.02%,質量堆積點xtip降低了23.8%,射流長度增加30.5%。所以,K裝藥可以有效提高射流頭部速度、射流質量,降低射流的質量堆積點,從而使射流拉得更長,破甲作用更大。但是,射流速度過高往往容易使射流斷裂,這樣對破甲作用是負面的。因此,上述對比可以說明錐形罩不適合K裝藥結構,有必要對K裝藥的藥型罩結構進行優化計算。

3 偏心亞半球罩桿流成型計算

3.1 偏心亞半球罩結構設計

目前,國內外研究人員在K裝藥中應用偏心亞半球形藥型罩較多[5-8],且其較容易形成桿式射流。為了便于與前面兩結構裝藥進行對比,本文采用藥型罩壁厚和高度不變的偏心亞半球形藥型罩,其參數為外半徑90 mm、壁厚2.2 mm、罩高67.73 mm、罩口徑50 mm,如圖5所示。理論研究偏心亞半球罩K裝藥桿式射流成型過程,優化計算理論程序的相關參數。

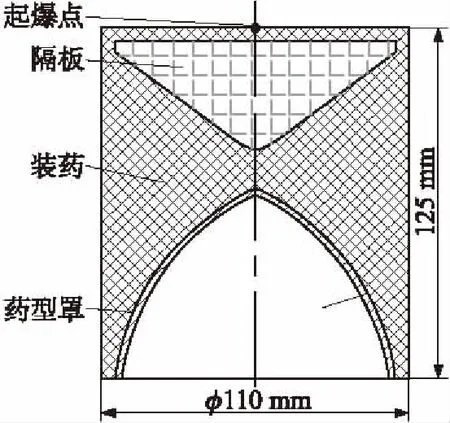
圖5 偏心亞半球罩K裝藥的結構示意圖

3.2 桿式射流成型計算

利用已優化的偏心亞半球罩結構參數來計算桿式射流的成型,理論計算結果與仿真結果如圖6所示,其中射流長度較傳統錐形罩裝藥提高了20.6%,射流頭部速度提高了22.3%,質量堆積點降低了41.3%。該結構的射流各參數提高的百分比比較合適,形成的射流速度較高,射流未發生斷裂,并且射流的質量堆積點更靠前,這對于射流的拉長是有利的。同時,射流的質量比更大,射流更均勻,這對提高射流的破甲作用也是有利的。

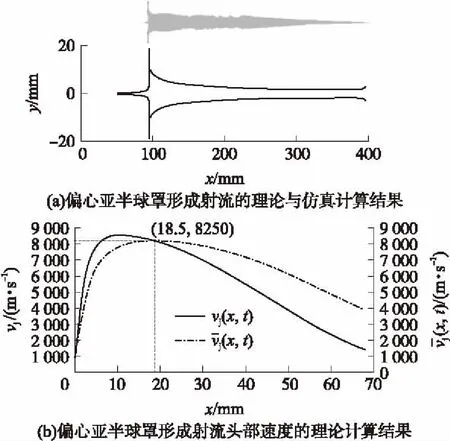
圖6 桿式射流成型理論與仿真計算結果對比(60 μs)

3.3 靜爆試驗

為了驗證理論與仿真計算結果,應用以上理論與仿真優化的偏心亞半球罩K裝藥結構進行靜爆試驗。偏心亞半球罩K裝藥結構如圖5所示,藥型罩實物與靜爆試驗現場布置如圖7(a)所示,試驗基準彈下部放置高度H1=265 mm的塑料炸高筒,其作用在于控制試驗彈的炸高。炸高筒下部放置2塊靶塊,每塊靶塊的長度均為250 mm,直徑為120 mm和150 mm 2種。最后試驗獲得了偏心亞半球罩K裝藥侵徹結果,如圖7(b)所示。由圖可見,偏心亞半球K裝藥形成的桿流對靶1與靶2開孔孔徑D1、D2較大且孔徑均勻、侵深ls較大。

圖7 偏心亞半球罩K裝藥試驗裝置與侵徹效果圖

偏心亞半球罩K裝藥侵徹結果的理論、仿真與試驗對比見表2,理論計算與試驗的侵深結果誤差為5.8%,驗證了本文建立的理論模型在小炸高條件下能較好地計算K裝藥射流成型及侵徹過程,具有一定的工程應用價值。

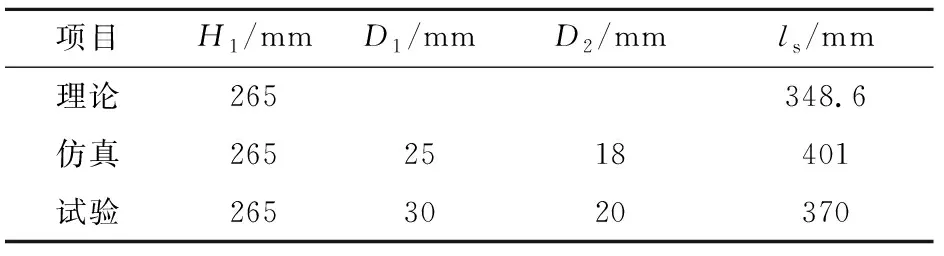
表2 偏心亞半球罩K裝藥實驗與仿真侵徹數據

4 結論

①本文基于改進的PER理論,并結合試驗數據與相關類別公式建立了K裝藥射流形成理論模型,通過Mathematica軟件編程計算射流成型過程。

②理論程序計算表明,相對于傳統錐形罩裝藥,同樣藥型罩結構的K裝藥形成射流的頭部速度提高了31.02%,質量堆積點降低了23.8%,射流長度增加了30.5%。

③優化設計的偏心亞半球罩K裝藥,形成了速度較高、質量比大、質量堆積點提前且更易拉長的桿流,并進行了靜爆試驗驗證,理論計算與試驗的侵深結果誤差為5.8%。

[1] 譚多望,孫承緯.成型裝藥研究新進展[J].爆炸與沖擊,2008,28(1):50-55.

TAN Duo-wang,SUN Cheng-wei.Progress in studies on shaped charge[J].Explosion and Shock Waves,2008,28(1):50-55.(in Chinese)

[2] CHANTERET P Y.Studies of maximum velocities for coherent shaped charge jets[C]//REINECKE W G.Proceeding of the 13th International Symposium on Ballistics.Lancaster:Technomic Publishing Co.Inc.,1992:463-472.

[3] MATTSSON K,CHURCH J.Development of the K-charge:a short L/D shaped charge[C]//REINECKE W G.Proceeding of the 18th International Symposium on Ballistics.Lancaster:Technomic Publishing Co.Inc.,1999:528-534.

[4] FOUNSTON R J,MATTSSON K V,OUYE N N.K charged:a multipurpose and shock warhead.UCRL-6393991B1[R].2002.

[5] 張先鋒,陳惠武.3種典型聚能射流侵徹靶板數值模擬[J].系統仿真學報,2007,19(19):4 399-4 410.

ZHANG Xian-feng,CHEN Hui-wu.Computional study of three typical shaped charge jets[J].Journal of System Simulation,2007,19(19):4 399-4 410.(in Chinese)

[6] 王樹有,趙有守.串聯攻堅戰斗部前級聚能裝藥研究[J].彈箭與制導學報,2005,25(3):501-508.

WANG Shu-you,ZHAO You-shou.Study of precursory shape of tandem warhead[J].Journal of Projectiles,Rockots,Missiles and Guidance,2005,25(3):501-508.(in Chinese)

[7] 張先鋒,陳惠武,何勇,等.反鋼筋混凝土串聯聚能裝藥技術研究[J].爆炸與沖擊,2008,28(3):207-212.

ZHANG Xian-feng,CHEN Hui-wu,HE Yong,et al.Study on a tandem shaped charge technique to reinforce concrete.[J].Explosion and Shock Waves,2008,28(3):207-212.(in Chinese)

[8] 王成,黃風雷.射流形式及其侵徹多層金屬靶的實驗研究[J].彈道學報,2002,14(4):50-54.

WANG Cheng,HUANG Feng-lei,Experimental and numerical simulation study on jet form and its penetration into multi-layer metal targets[J].Journal of Ballistics,2002,14(4):50-54.(in Chinese)

[9] 王樹魁,貝靜芬.成型裝藥原理及其應用[M].北京:兵器工業出版社,1992:51-67.

WANG Shu-kui,BEI Jing-fen.Shape charge and principle[M].Beijing:Ordance Industry Press,1992:51-67.(in Chinese)

[10] 魏惠之,朱鶴松.彈丸設計理論[M].南京:南京理工大學,1991.

WEI Hui-zhi,ZHU He-song,The theory of warhead[M].Nanjing:Nanjing University of Science and Technology,1991.(in Chinese)

[11] CHOU P C,CARLEONE J,HIRSCH E,et al.Improved formulas for velocity,acceleration,and projection angle of explosively driven liners[C]//Proceedings of the 6th International Symposium on Ballistics.Orlando,FL:IBC,1981:27-29.

[12] 趙國志,張運法,王曉鳴.戰術導彈戰斗部毀傷作用機理[M].南京:南京理工大學,2002:15-28.

ZHAO Guo-zhi,ZHANG Yun-fa,WANG Xiao-ming.The tactical missile warhead damage mechanism[M].Nanjing:Nanjing University of Science and Technology,2002:15-28.(in Chinese)

[13] 黃風雷,段衛東.爆炸驅動下飛板運動速度的實驗研究[J].爆炸與沖擊,2002,22(1):26-29.

HUANG Feng-lei,DUAN Wei-dong.Experimental investigation on flying-plate velocity under blasting driving[J].Explosion and Shock Waves,2002,22(1):26-29.(in Chinese)

[14] KIWAN A R,WISNIEWSKI H.Theory and computations of collapse and jet velocities of metallic shaped charge liners[R].MD,USA:US Army Ballistic Research Lab Aberdeen Proving Ground,1972.

[15] 張攀軍,李偉兵,王曉鳴,等.網格密度對聚能侵徹體成型有限元仿真的影響[J].彈箭與制導學報,2011,31(3):111-116.

ZHANG Pan-jun,LI Wei-bing,WANG Xiao-ming,et al.The effect of grid density on simulation of penetration formation[J].Journal of Projectiles,Rockets,Missiles and Guidance,2011,31(3):111-116.(in Chinese)