橡膠軸承-轉軸系統碰摩響應動力學特性研究

花純利， 塔 娜， 饒柱石

(上海交通大學 振動、沖擊噪聲研究所 機械系統與振動國家重點實驗室，上海 200240)

轉軸系統廣泛用于實際工程。為提高轉軸系統機械效率，將轉軸與軸承間隙設計的越來越小，但會使轉軸系統發生碰摩的可能性提高。轉軸與軸承間發生碰摩將致轉軸系統局部發熱甚至嚴重磨損，誘發機械劇烈振動，嚴重時會出現反向渦動失穩造成整個機械系統破壞。因此，研究轉軸系統的碰摩復雜非線性動力學行為、確定其與系統參數間關系、揭示系統穩定性邊界條件，對優化轉軸系統設計與故障診斷意義甚為重要。

對轉軸系統碰摩研究已有大量成果。自上世紀80年代以來，在實驗、數值模擬、理論分析等方面對轉子系統碰摩響應特性進行廣泛深入研究。如同頻全周碰摩運動、“跳躍”現象[1-6]，準周期局部碰摩運動[7]及混沌行為[8-10]。文獻[11-13]中所用模型雖與本文相似，但其接觸力為線性模型且未深入討論偏心率對系統動態特性影響，亦未解釋、闡明跳躍現象產生的條件。文獻[2]亦用兩自由度轉子模型，但其定子具有耦合剛度且接觸力為線性模型。止今，大部分研究主要集中在將軸承簡化為無質量線性彈簧的轉軸碰摩模型上，但該簡化不能充分反映具有超彈性材料特性的橡膠軸承動態特性。國內外船舶及深井泵等設備中因大量使用橡膠軸承，致使橡膠體磨損嚴重。此與螺旋槳軸承支承的整個轉子系統靜態特性與動力響應密切相關。由于對橡膠軸承支撐的轉軸/軸承系統研究較少，且對全面考慮碰摩主要參數的非線性彈性支撐的轉軸/軸承系統模型動力學特性認識不足，尤其對轉軸/軸承偏心率及阻尼比對系統動力響應所致影響了解更少。因此，本文以橡膠軸承支撐的轉軸/軸承系統為對象，將其簡化為非線性彈性支撐的轉軸/軸承系統進行研究，并分析該模型動力學特性。即分析轉軸系統發生碰摩、鞍結分叉及Hopf分叉的邊界條件，討論阻尼比與偏心率等系統參數對系統穩定性影響。

1 模型與運動控制方程

橡膠軸承/轉軸系統示意圖見圖1，橡膠軸承由軸承襯套與橡膠襯套兩部分組成。將其簡化成Jeffcott轉子系統，見圖2，轉軸簡化為一支撐在無質量剛度k，阻尼c，轉軸中間質量m的剛性轉軸上，轉軸與軸承間間隙δ，轉軸質心與幾何中心偏心距e。

圖1 轉軸/軸承系統示意圖

圖2 Jeffcott轉軸/軸承系統模型

考慮橡膠軸承具有的非線性特征，計入支承剛度的非線性特性。由于軸系的橡膠艉軸承均為新設計產品，未經實驗測得準確剛度曲線。因此，其非線性載荷-變形關系參照德國國防軍艦艇建造規范(BV043)進行估算：

F=krr(1+100r)=krr+αr2

(1)

其中：F為載荷(N)；r為變形量(m)；kr為軸承剛度值(N/m)。故軸承內環面上轉軸/軸承接觸剛度為kr+αr。則轉軸與軸承間的摩擦力及接觸力為：

(2)

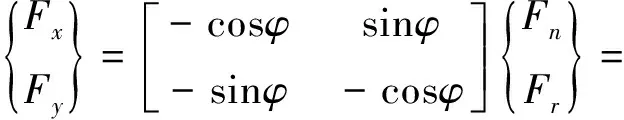
(3)

橡膠軸承/轉軸系統動力學方程可表達為：

(4)

式中：Θ為heaveside函數，即：

將橡膠軸承/轉軸系統動力學方程無量綱化：

(5)

轉軸旋轉過程中，轉軸與軸承接觸、不接觸狀態均有穩定的周期解。設其解的形式為：

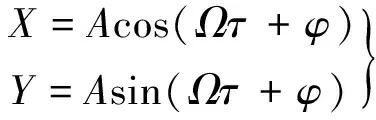
(6)

在軸承與轉軸未發生接觸狀態下Θ=0，將式(6)代入控制方程并求解得幅值、相位角分別為：

(7)

由于軸承與轉軸間隙有限，故非接觸狀態下所求幅值A須滿足A≤1條件。即：

(ρ2-1)Ω4+2(β-2ξ2)Ω2-β2≤0

(8)

通過求解式(8)可兩實根Ωl，Ωu，且記為線性轉軸開始發生碰摩時低、高轉速。當Ω<Ωl或Ω>Ωu時，轉軸系統存在無碰摩同頻周期響應。

軸承與轉軸發生接觸狀態下Θ=1，將式(6)代入式(5)得關于振動幅值A的方程式：

a4A4+a3A3+a2A2+a1A+a0=0

(9)

其中：

a4=g2+g2f2

a3=2g[(1-2g+β-Ω2)+f(2ξΩ+f-2gf)]

a2=(1-2g+β-Ω2)2+(2ξΩ+f-2gf)2+

2g(g-1)(1+f2)

a1=2(g-1)[(1-2g+β-Ω2)+f(2ξΩ+f-2gf)]

a0=(g-1)2(1+f2)-ρ2Ω4。

一元四次方程最多有兩個互異的正實數根，復數與負數實根均無實際意義。在式(5)Θ=1條件下，方程有二重正實根時，即為系統鞍結分叉的邊界條件。為保證軸承與轉軸處于接觸狀態，幅值A不僅需滿足正實數條件且需滿足幅值A>1。

2 周期解穩定性分析

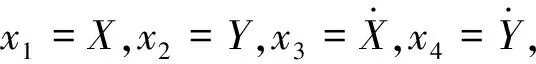
(10)

(11)

式中：

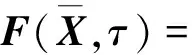
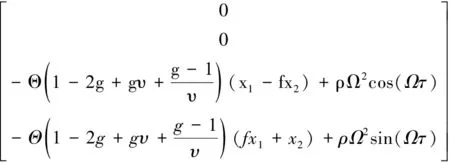
為簡便，引入穩態周期解形式：

(12)

其中：A為非接觸狀態下式(7)與接觸狀態下式(9)的穩定周期解。

通過解式(11)得：

(13)

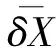
當Θ=0時轉軸與軸承處于非接觸狀態，雅可比方程J恰好是矩陣B，對應的特征方程為|B-λI|=0，將其展開：

λ4+4ξλ3+(2β+4ξ2)λ2+4ξβλ+β2=0

(14)

根據Routh-Hurwitz(勞斯-霍爾維茨)穩定性判據，式(5)(Θ=0時)非接觸狀態解的穩定性條件為：

ξ>0

(15)

由式(15)知，當系統阻尼為正阻尼時，對應的周期解是穩定的。當系統振動幅值大于間隙δ時，軸承與轉軸會發生碰摩。此時轉軸系統控制方程中Θ=1。式(5)的解將為非線性的周期解。其雅可比矩陣J可表達為：

(16)

式中：

由式(16)知，雅可比矩陣J為周期性的時間依賴矩陣，不能直接推導、分析其解的穩定性，需作變換：

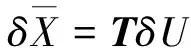
(17)

式中：轉換矩陣T為：

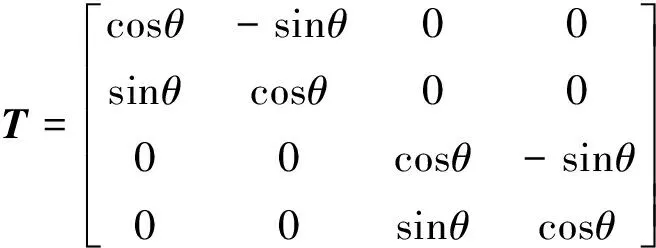
將式(17)代入式(13)，得：

(18)

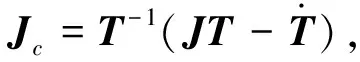
(19)

式(19)表明雅可比矩陣Jc與時間參數無關。δU解與式(11)解的穩定性取決于矩陣Jc特征值實部符號。對應的特征方程滿足|Jc-λI|=0，將其展開為：

b4λ4+b3λ3+b2λ2+b1λ+b0=0

(20)

其中：

b4=1

b3=4ξ

諸多系數均為幅值A的函數，故Routh-Hurwitz(勞斯-霍爾維茨)穩定性判據可用于判斷式(11)非線性穩態周期解的穩定性。

基于分叉理論,分析周期解的分叉邊界，給出參數空間穩定區域。若雅可比矩陣Jc有一零特征值，系統將出現鞍結分叉，此時式(20)中b0=0，即：

(21)

通過消除幅值A的符號計算，同時求解式(9)、(21)獲得關于Ω的12次多項式。求解參數方程，可得式(9)發生鞍結分叉條件的參數空間。全周碰摩解的鞍結分叉點處幅值A為大于1的正實數。

基于Hopf分叉理論，系統會有一對共軛純虛數特征值。將λ=+iωυ代入式(20)得：

(22)

消去參數ωυ得(代入λ=-iωυ得同樣結果)：

(23)

需滿足不等式：

b1/b3>0

(24)

用式(9)、(23)消去幅值A，求解參數方程，可得系統發生Hopf分叉的邊界線HF。同頻全周碰摩解Hopf分叉點處幅值A為大于1的正實數。

3 系統參數對轉軸響應影響

由式(15)知，轉軸系統在無碰摩狀態下周期解總是穩定的，但轉軸與軸承間間隙有限，因此周期解不可能在系統的所有參數下一直存在。由式(8)及分析知，線性橡膠軸承/轉軸系統激振頻率分別由高、低轉速趨向系統固有頻率時，系統振動幅值A會在Ω=Ωl與Ω=Ωu處趨近1。當轉軸/軸承系統處于接觸狀態、激振頻率分別向低、高轉速變化時，系統振動幅值A會在Ω=SNl與Ω=SNu處趨近1。由式(9)、(21)知，碰摩狀態存在于轉速SNl與SNu之間，SNl與Ωl基本相等，SNu與Ωu或相等或不等，取決于系統參數，兩者不等時系統振動幅值將隨轉速的變化出現跳躍現象。如將曲線Ω=Ωl，Ω=Ωu，Ω=SNl，Ω=SNu，Hopf分叉邊界HF繪制于(Ω,ξ)平面，則該平面將被分隔成若干部分，不同部分代表系統不同運動狀態，即(A)，(B)為無碰摩周期運動；(C)為同頻全周碰摩運動；(D)為局部碰摩運動及反向渦動失穩運動；(E)為無碰摩周期運動及同頻全周碰摩運動共存，即處于接觸狀態條件下系統做同頻全周碰摩運動，而處于非接觸狀態條件下系統做無碰摩周期運動；(F)為無碰摩周期運動、局部碰摩運動或反向渦動失穩運動，即處于接觸狀態條件下系統做局部碰摩運動或反向渦動失穩運動，而處于非接觸狀態條件下系統做無碰摩周期運動。

對不同參數取值下系統運動狀態演變過程分別進行討論。取偏心率ρ=0.8，系統各參數分別為：f=0.2,β=0.5，g=0.01。此時曲線Ω=Ωl，Ω=Ωu，Ω=SNl，Ω=SNu，分叉邊界HF將(Ω,ξ)平面分成四部分，轉軸系統在轉速Ω，阻尼比ξ參數平面內系統響應特性區域見圖3。因Ωl=SNl，Ωu=SNu，系統不會發生跳躍現象。由圖3知，在區域(C)內轉軸系統做同頻全周碰摩運動，在區域(D)內系統做非穩定周期碰摩運動。

將系統偏心率減小為ρ=0.5時，轉軸系統響應穩定區域發生明顯變化，見圖4。

與偏心率ρ=0.8情況相比，系統響應特性在(Ω,ξ)平面內發生顯著變化，邊界Ω=Ωl=SNl向右移動，邊界Ω=Ωu與Ω=SNu向左移動，且曲線Ωu，SNu不重合。Hopf分叉邊界線HF無明顯變化。因此，非穩定碰摩響應區域(D)及同頻全周碰摩運動區域(C)的兩側邊界向中間靠攏而縮小，表明系統出現全周碰摩轉速范圍變小；出現同頻全周碰摩運動與無碰摩周期運動共存區域(E)及無碰摩周期運動、局部碰摩運動或反向渦動失穩運動區域(F)。此時轉軸系統同頻全周碰摩運動會存在于Ω=Ωl與Ω=SNu區間內；區間Ω>Ωu存在無碰摩周期運動，故在區間Ωu，SNu間同頻全周碰摩運動與無碰摩周期運動均可能存在。當轉軸系統轉速Ω發生變化時會有跳躍現象發生。

由討論可知，偏心率降低會使碰摩區域發生明顯變化并出現跳躍現象，因此，需進一步討論其對轉軸系統響應影響。轉軸系統在(Ω,ρ)平面的響應特性見圖5。

圖3 轉軸碰摩響應在(Ω, ξ)平面穩定區域圖(ρ=0.8)

由式(8)所得Ωu，Ωl值可給出轉軸與軸承由無接觸向接觸過渡時臨界轉速上、下邊界。由圖5看出，①系統共振振幅小于轉軸與軸承間間隙即ρ<0.17時，轉軸與軸承間不發生碰摩；隨偏心率的增加Ωl逐漸減小而Ωu卻逐漸增大，因此Ωl與Ωu間區域增大，即發生碰摩的轉速區間增大。②同理可得轉軸與軸承由接觸狀態向脫離接觸狀態過渡時轉速的上、下邊界值SNu及SNl，而Ωl與SNl總相等；Ωu與SNu在0.17<ρ<0.65范圍內不相等，該區域內轉軸系統振幅隨轉速的變化會發生跳躍現象，且隨偏心率的增加發生跳躍現象的轉速區間呈現先增大后減小直至消失的趨勢；③由于轉軸系統Hopf分叉邊界HF與鞍結分叉邊界SNu在ρ=0.3處相交一點，ρ>0.3時，隨偏心率的增加，開始發生Hopf分叉的轉速Ω逐漸減小，導致落在區域(E)內的轉速區間不斷縮小并最終消失；0.17<ρ<0.3時，系統不會出現Hopf分叉及失穩現象，只會出現無碰摩周期運動、同頻全周碰摩運動或兩運動狀態跳躍轉變現象。

4 結 論

本文對軸承簡化為非線性彈性支撐轉軸系統發生周期無碰摩運動與同頻全周碰摩運動存在的區域及穩定性進行研究，并分析阻尼比及偏心率等系統參數對轉軸系統動態特性影響、對不同轉軸系統響應特性邊界條件影響。結論如下：

(1)轉軸系統Hopf分叉邊界HF為轉速、摩擦系數、阻尼比及偏心率的函數。Hopf分叉邊界將碰摩響應區域劃分成同頻全周碰摩響應區域與局部碰摩運動、反向渦動失穩運動區域兩部分。

(2)阻尼比是影響轉軸碰摩響應的主要參數之一。大阻尼比系數下，轉軸系統響應主要為無碰摩周期運動、同頻全周碰摩運動及兩種響應共存；小阻尼比系數會出現不穩定碰摩運動。因此，大阻尼比轉軸系統更穩定。

(3)偏心率是轉軸系統重要參數之一，偏心率小轉軸系統穩定。偏心率小至轉軸系統共振幅值小于間隙時，轉軸與軸承間不發生碰摩。隨偏心率的增加轉軸與軸承會在某狀態下發生碰摩；小偏心率時，系統有周期無碰摩運動及同頻全周碰摩運動且會發生在兩運動狀態間跳躍現象，較大偏心時系統會在某轉速下發生Hopf分叉,且隨偏心率的增大,發生Hopf分叉所需轉速會降低。

參 考 文 獻

[1]Ehrich F F. High order sub-harmonic response of high speed rotors in bearing clearance[J]. Journal of Vibration, Acoustics, Stress, and Reliability in Design, 1988, 110: 9-16.

[2]Jiang J,Ulbrich H. Stability analysis of sliding whirl in a nonlinear jeffcott rotor with cross-coupling stiffness coefficients[J]. Nonlinear Dynamics,2001,24(3):269-283.

[3]Zhang H B, Chen Y S, Li J. Bifurcation on synchronous full annular rub of rigid-rotor elastic-support system[J]. Applied Mathematics and Mechanics,2012,33(7):865-880.

[4]Zhang H B, Chen Y S. Bifurcation analysis on full annular rub of a nonlinear rotor system [J]. Science China Technological Sciences, 2011, 54(8): 1977-1985.

[5]Shang Z Y, Jiang J, Hong L. The global responses characteristics of a rotor/stator rubbing system with dry friction effects [J]. Journal of Sound and Vibration, 2011, 330(10) :2150-2160.

[6]李朝峰，戴繼雙，聞邦椿. 油膜支撐雙盤轉子-軸承系統周期運動穩定性與分岔[J]. 力學學報,2011,43(1):208-216.

LI Chao-feng, DAI Ji-shuang, WEN Bang-chun. Stability and bifurcation of the rotor-bearing system with double disks supported by cylindrical bearings[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(1):208-216.

[7]Kim Y B, Noah S T. Quasi-periodic response and stability analysis for a nonlinear jeffcott rotor[J]. Journal of Sound and Vibration, 1996, 190(2): 239-253.

[8]Goldman P, Muszynska A. Chaotic behavior of rotor/stator system with rubs[J]. Journal of Engineering for Gas Turbines and Power, 1994, 116: 693-701.

[9]Evgueni V K, Wiercigroch M, Cartmell M P. Regular and chaotic dynamics of a discontinuously nonlinear rotor system[J]. Chaos,Solitons and Fractals,2002,13(6): 1231-1242.

[10]褚福磊, 張正松, 馮冠平. 碰摩轉子系統的混沌特[J]. 清華大學學報( 自然科學版),1996,36(7):52-57.

CHU Fu-lei, ZHANG Zheng-song, FENG Guan-ping. Chaotic behavior of a rub rotor model[J]. Journal of Tsinghua University ( Sci & Tech), 1996,36(7):52-57.

[11]劉 林, 江 俊. 轉子/定子碰摩響應的全局動力學特性研究[J]. 應用力學學報,2006, 23(3):351-356.

LIU Lin, JIANG Jun. Global dynamical characteristics of rotor/ stator rubbing [J]. Chinese Journal of Applied Mechanics, 2006, 23(3):351-356.

[12]Zhang W M, Meng G. Nonlinear dynamics of a rub-impact micro-rotor system with scale-dependent friction model [J]. Journal of Sound and Vibration, 2008, 309(3-5): 756-777.

[13]張義民, 劉巧伶, 聞邦椿. 旋轉機械系統碰摩故障的失效靈敏度研究[J]. 振動工程學報,2007,20(2):189-193.

ZHANG Yi-min, LIU Qiao-ling , WEN Bang-chun. Failure sensitivity investigation in impact-rub malfunction for rotating machinery[J].Journal of Vibration Engineering,2007, 20(2):189-193.