齒輪減速器振動噪聲預估公式定制方法研究

周建星, 孫文磊, 萬曉靜

(1.新疆大學 機械工程學院,烏魯木齊,830047; 2.新疆大學 機械工程博士后流動站,烏魯木齊,830047)

隨著現代工業化程度的不斷提高，振動噪聲問題也越來越受到重視。工業設施的振動噪聲不僅會引起噪聲污染，還影響著設備的穩定性及操作舒適性。在汽車領域，NVH已成為汽車業各大制造企業重點關注的問題之一；對于武器載體(如艦船等)振動噪聲將直接影響到其隱蔽性及戰斗力。

齒輪傳動具有效率高，結構緊湊，工作可靠，壽命長等特點，廣泛應用于各工業領域中。由于齒輪的結構特性，在其嚙合過程中不可避免地存在著齒輪嚙合剛度的波動及誤差作用，使傳動系統發生振動，并通過軸承傳遞于箱體，不僅影響系統的整體的動態性能，還產生噪聲污染。減速器振動噪聲研究經歷了從定性判斷到定量分析的過程，上世紀60年代起，為了簡化計算齒輪減速器的振動噪聲，Nakamura、Niemann、Kato及Masuda等先后開展了噪聲預估公式的研究，他們通過大量的試驗測試，總結了減速器輻射噪聲的變化規律，提出了一些簡化計算方法[1-4]，并得到了一定的推廣和應用，但其計算準確性上仍存在不足；90年代以來，有限元法、邊界元法和無網格等工程計算方法逐漸完善，為噪聲預測提供了有效支持[5-7]。在對齒輪減速器振動噪聲方面的研究中，以FEM/BEM方法使用最為廣泛。文獻[8-10]采用FEM/BEM方法對減速器振動噪聲進行預測，并通過實驗得到了較好的驗證。但是減速器振動噪聲的數值預估不僅需要較為細致的減速器結構特征以及相關工程經驗，求解過程還要消耗大量計算資源，不便于工程設計階段的使用。

本文以單級齒輪減速器為研究對象，通過FEM/BEM仿真的方法分析了齒輪減速器振動噪聲隨齒輪精度等級的變化，綜合考慮誤差與轉速和負載的耦合作用關系，擬合得到了考慮齒輪精度等級的減速器噪聲預估公式，并通過實驗對其準確性進行了驗證。

1 減速器噪聲預估方法

1.1 經驗預估方法

1965年，為了預測齒輪傳動系統的振動噪聲， Niemann提出了減速器噪聲與20logW(W為傳動功率)成線性比例關系，并擬合了單級減速器噪聲強度的經驗公式：

L=50+20logW+∑K

(1)

式中：L為噪聲強度(dB)；W為傳遞功率(hp)；K為修正值。

1975年，Kato按照Niemann的思路，考慮了傳動功率、速度、重合度、傳動比、螺旋角、精度等級對減速器輻射噪聲的影響，提出了以下的半經驗公式：

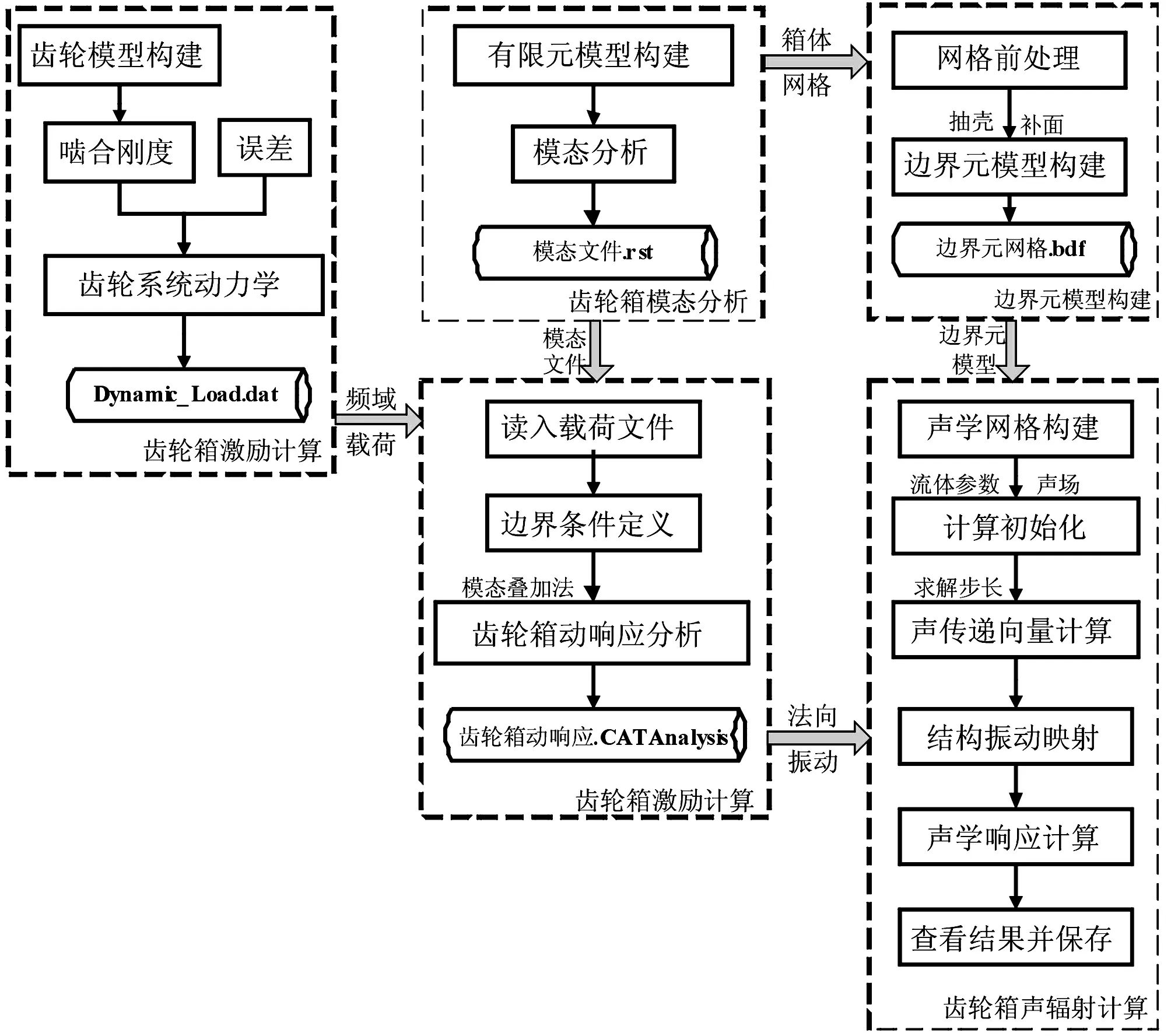
圖1 FEM/BEM噪聲輻射求解流程

由于Kato公式形式簡單，并可以定量地計算出齒輪副的噪聲值，在工程設計中得到了一定的應用。但由于公式中無法對齒輪誤差形式及齒輪精度對減速器噪聲的影響進行合理的體現，故其計算結果僅在少數情況下與實驗結果吻合較好。

1.2 FEM/BEM噪聲輻射分析方法

在進行聲場邊界元分析時，一般是以結構表面法向振動加速度作為邊界條件，而這些數據主要是通過其他數值方法(如有限元法)計算或者通過試驗測得，分析流程如圖1所示。首先采用合理的方式對齒輪副時變嚙合剛度及誤差等激勵進行等效，并建立齒輪系統動力學模型，以求解作用于齒輪箱上的動載荷；其次，建立齒輪箱有限元模型，求解齒輪箱結構穩態動響應，并得到齒輪箱表面振動信息；然后，建立齒輪箱聲學邊界元模型；最后，以結構體表面的法向速度作為邊界條件對齒輪箱噪聲輻射進行分析。

若能合理的對減速器振動激勵進行等價，求取軸承動載荷，則FEM/BEM方法可以有效求解減速器噪聲輻射。

2 減速器振動噪聲數值計算

2.1 分析模型

分析模型參數如表1所示。

表1 分析模型參數

分析模型如圖2所示，為單級直齒圓柱齒輪減速器，模型構建時，對結構中存在的較小的倒角及細小特性進行了適當簡化。

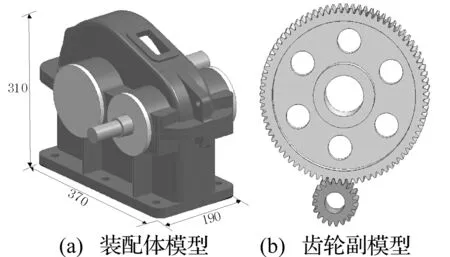
圖2 減速器模型

2.2 齒輪箱激勵計算

減速器運轉過程中，由于齒輪時變嚙合剛度及誤差激勵的作用，使齒輪動態嚙合力產生波動，從而引起系統振動。

對齒輪嚙合剛度引入有限元接觸算法，采用真實齒輪模型，計算得到在嚙合線方向上由齒輪輪體，輪齒彈性變形及赫茲接觸變形組成的總變形μ。而在該位置的嚙合剛度為：

K=T/Rbu

(3)

其中：Rb為齒輪基圓半徑；T為負載扭矩。

將一個嚙合周期劃分為若干等分，分別求取各嚙合位置上的剛度。對于其他位置則采用樣條插值得到，齒輪時變嚙合剛度曲線如圖3所示，基本成矩形波形式。

對于誤差激勵，可以采用簡諧函數對其進行模擬，并假設在一個嚙合周期中，誤差為正弦分布如圖3所示，將輪齒誤差表示為：

e(t)=ersin(ωt/Tm+φ)

(4)

式中：er為誤差幅值，Tm為齒輪嚙合周期，ω為主動輪轉速，φ為相位角。

2.3 傳動系統模型構建

傳動系統動力學模型如圖3所示，其中p為主動輪，g為從動輪。由于傳動軸兩軸承間跨度較短，彎曲剛度較大，故不考慮其彎曲變形，因此可將軸承支撐剛度和阻尼用等效值kyp，kyg和cyp，cyg來表示。系統共包含4個自由度，分別為:

yp為主動輪p平移位移；θp為主動輪p轉動位移；

yg為從動輪g平移位移；θg為從動輪g轉動位移；

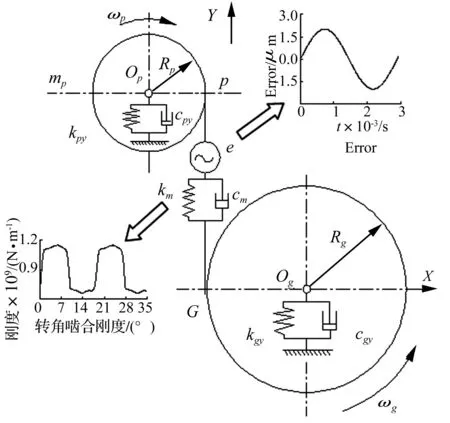
圖3 齒輪副動力學模型

輪副的嚙合力和嚙合阻尼力，可表示為：

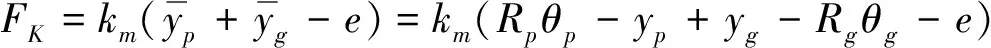
式中，km為齒輪嚙合剛度，cm為齒輪嚙合阻尼，e為嚙合誤差，Rp、Rg分別為主從動輪基圓半徑。

因此齒輪副動態嚙合力Fpg為：

Fpg=Fk+Fc

(5)

依據各齒輪受力平衡關系有：

(6)

式中：mp為主動輪質量，mg為從動輪質量，Tp為輸入扭矩，Tg為輸出扭矩。

方程的矩陣形式為：

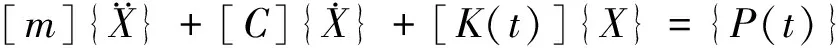
(7)

式中：M、C、K為質量陣、阻尼陣及剛度陣;X為位移向量;P為廣義力向量

2.4 減速器振動噪聲計算

齒輪箱動響應分析模型如圖4所示。采用4面體單元進行網格劃分，模型共劃分節點38 634個，單元146 238個，箱體材料為鑄鋼，定義彈性模量E=207 GPa，泊松比υ=0.3，密度ρ=7 800 kg/m3。

作用于輸出軸和輸入軸的動載荷通過軸承傳遞于箱體，在主從動輪軸承支承位置建立中心節點，與軸承壁面節點建立耦合關系，將動載荷施加于中心節點。

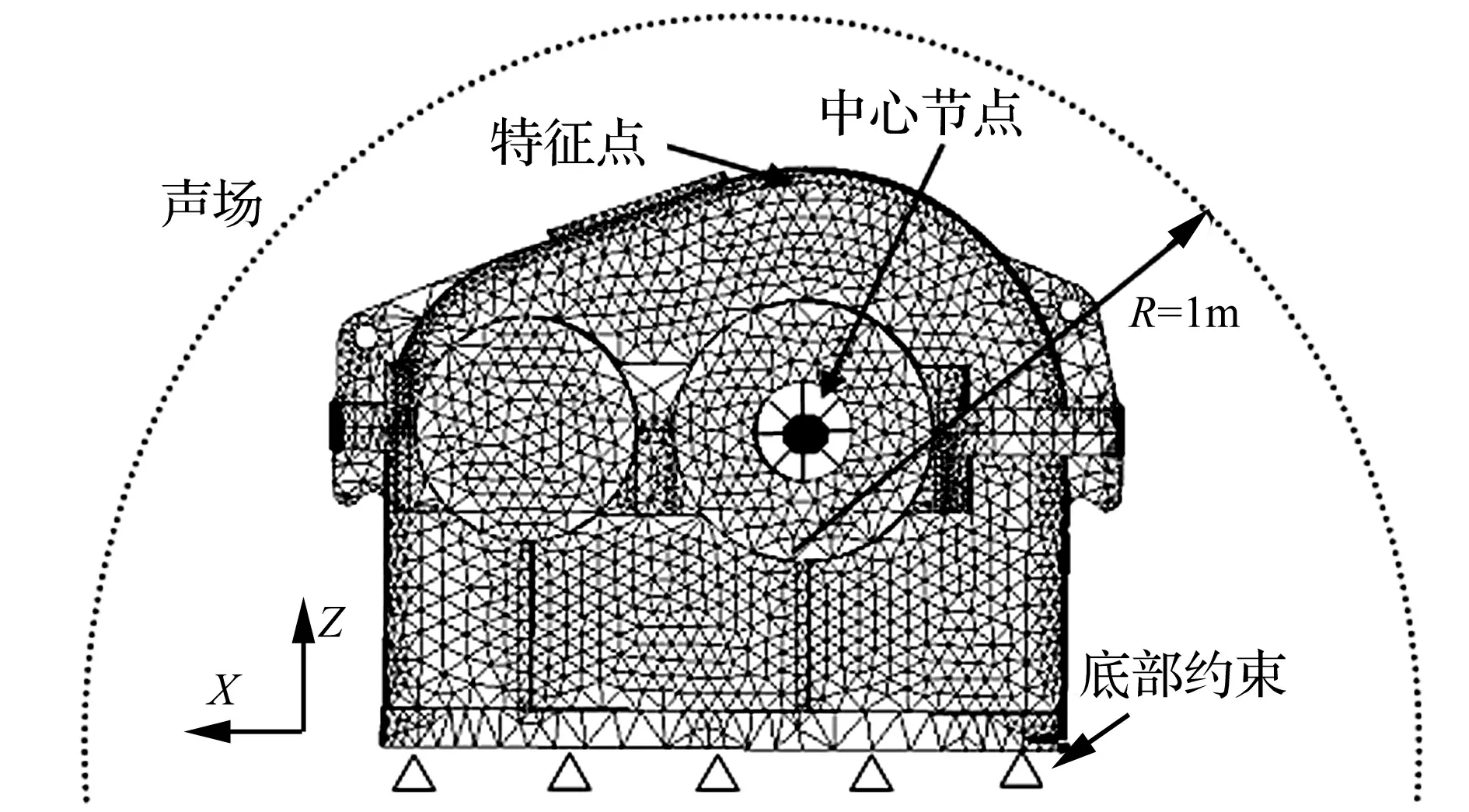
圖4 箱體有限元模型

采用Lanczos法對齒輪箱進行模態計算，齒輪箱固有頻率如表2所示。

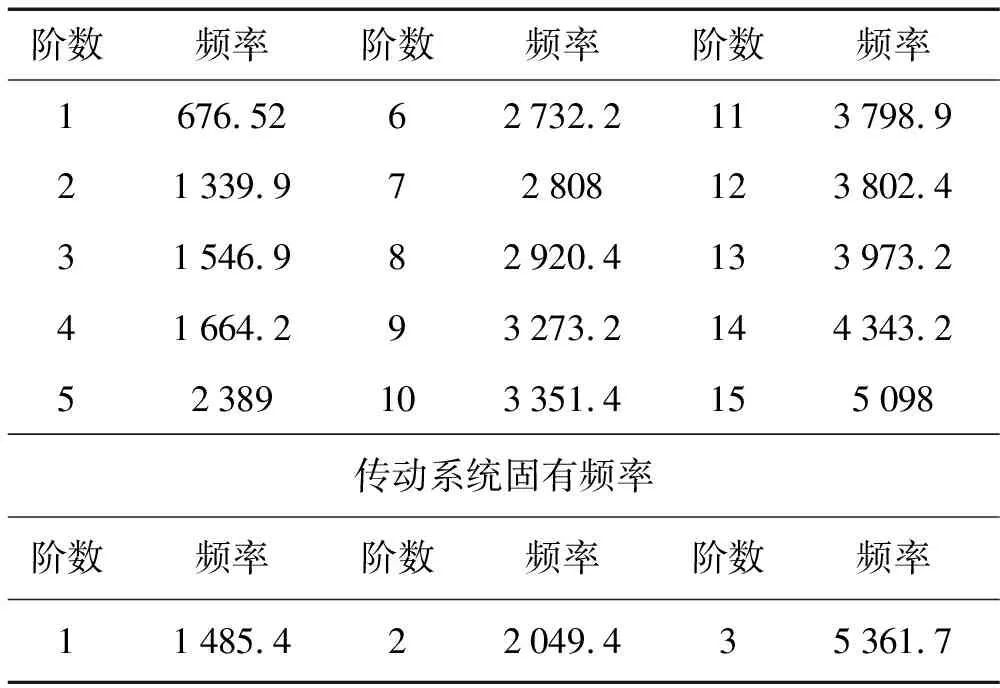
表2 減速器固有頻率(Hz)

采用自主研發的一套結構動響應計算流程對齒輪箱動響應進行求解(求解流程詳見[11])，得到了齒輪箱結構動響應，以齒輪箱外表面法向振動加速度為邊界，采用BEM方法求解齒輪箱噪聲輻射。為保證數據輸入的正確性，邊界元網格與有限元網格采用相同的劃分方式，以保證兩種模型節點間數據傳遞的穩定性。

在不考慮誤差時，齒輪箱噪聲譜如圖5所示，由于齒輪箱以扭轉振動為主，頂部法向振動分量不大，故頂部場點噪聲明顯小于兩側；軸承兩側場點呈對稱分布，其聲壓級分布曲線基本一致，并均在齒輪嚙合頻率的2倍頻，4倍頻及5倍頻位置處產生了峰值，最大峰值出現在二倍頻及五倍頻位置，為50 dB。

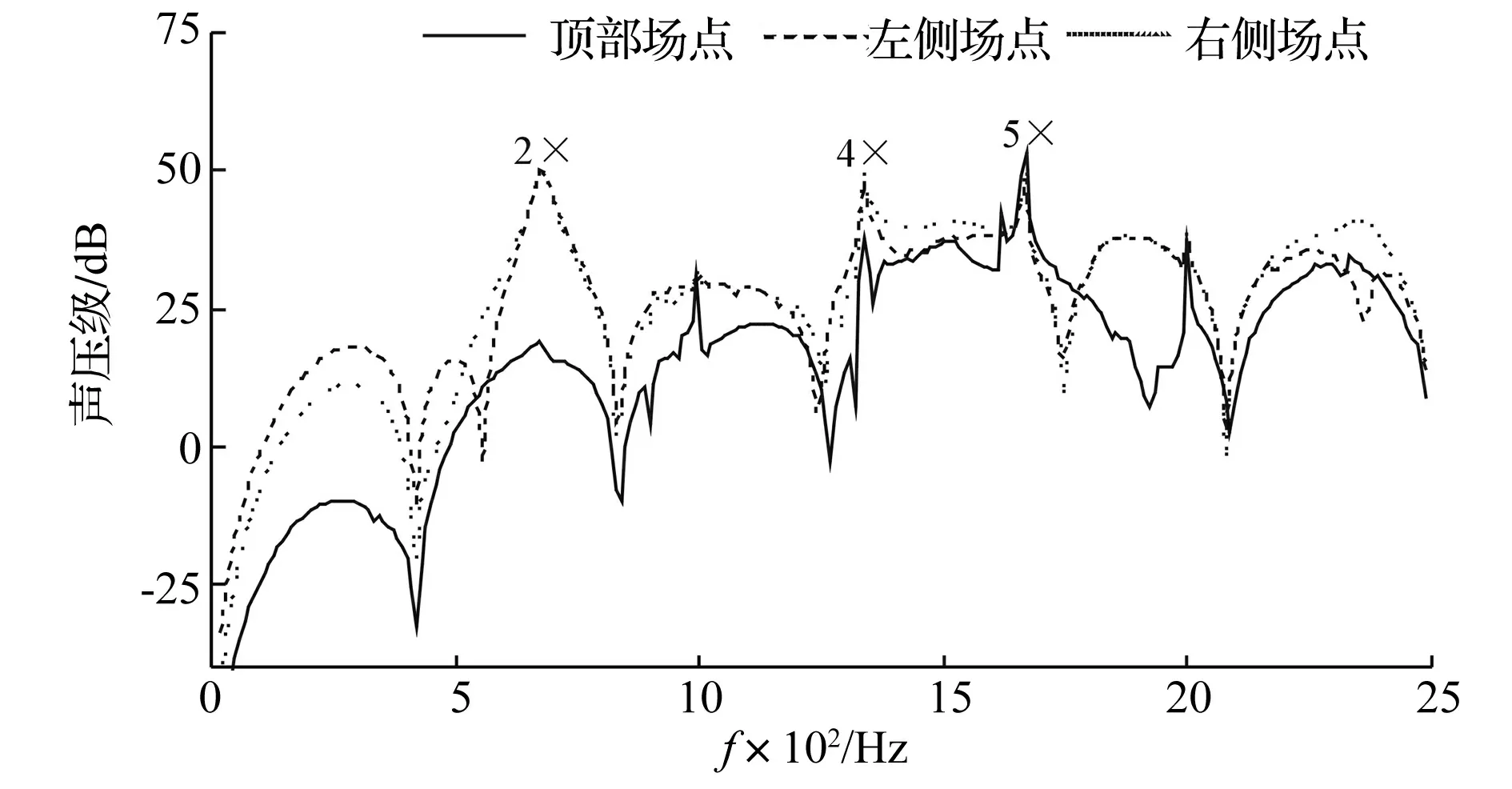
圖5 不同位置的箱體噪聲譜

由式(8)可計算各場點等效聲壓級:

(8)

其中：P(t)為時刻t的聲壓；P0為參考聲壓；T為求解周期。

采用Kato公式計算可以得到齒輪箱輻射噪聲為46.88 dB，通過FEM/BEM方法計算得到齒輪箱各場點噪聲分布在41 dB～50 dB之間，故可認為在不考慮誤差時，兩種方法計算結果具有一致性。

3 計算模型匹配性分析

通過上述分析，可認為算例中減速器在其額定工況下輻射噪聲與Kato公式計算結果基本一致，但在修正前還需對分析模型與Kato計算模型的匹配性進行分析，本文主要從減速器噪聲輻射隨轉速及負載的變化兩個方面來說明其變化規律的一致性。

3.1 轉速對噪聲輻射的影響

本文計算了減速器常規工作轉速(即500～3 000 r/min)的噪聲輻射，并采用瀑布圖的方式進行表述，如圖6所示，其中fb1為齒輪箱1階固有頻率，fm為齒輪副嚙合頻率。顏色較深的區域代表噪聲輻射較大的位置，可以看到在低速時齒輪箱噪聲譜各頻率成分均不大，隨著轉速的增加，噪聲輻射逐漸強烈。

各轉速在齒輪嚙合頻率及其倍頻位置，均產生了放射狀深色區域，但并不明顯。在與齒輪箱固有頻率較為接近的670 Hz附近，1 300 Hz～1 700 Hz位置以及3 000 Hz～4 000 Hz位置均產生了深色區域，其中由于箱體第二、三、四階固有頻率對激勵較為敏感且振動能量較大，故各轉速下在該頻帶產生了強烈的共振區；同時，齒輪箱結構第一階固有頻率及在3 000 Hz～4 000 Hz位置的振型在軸承激勵作用下雖然振動能量不大，但其相對法向振動也較強，故在該頻帶噪聲輻射也較為強烈。

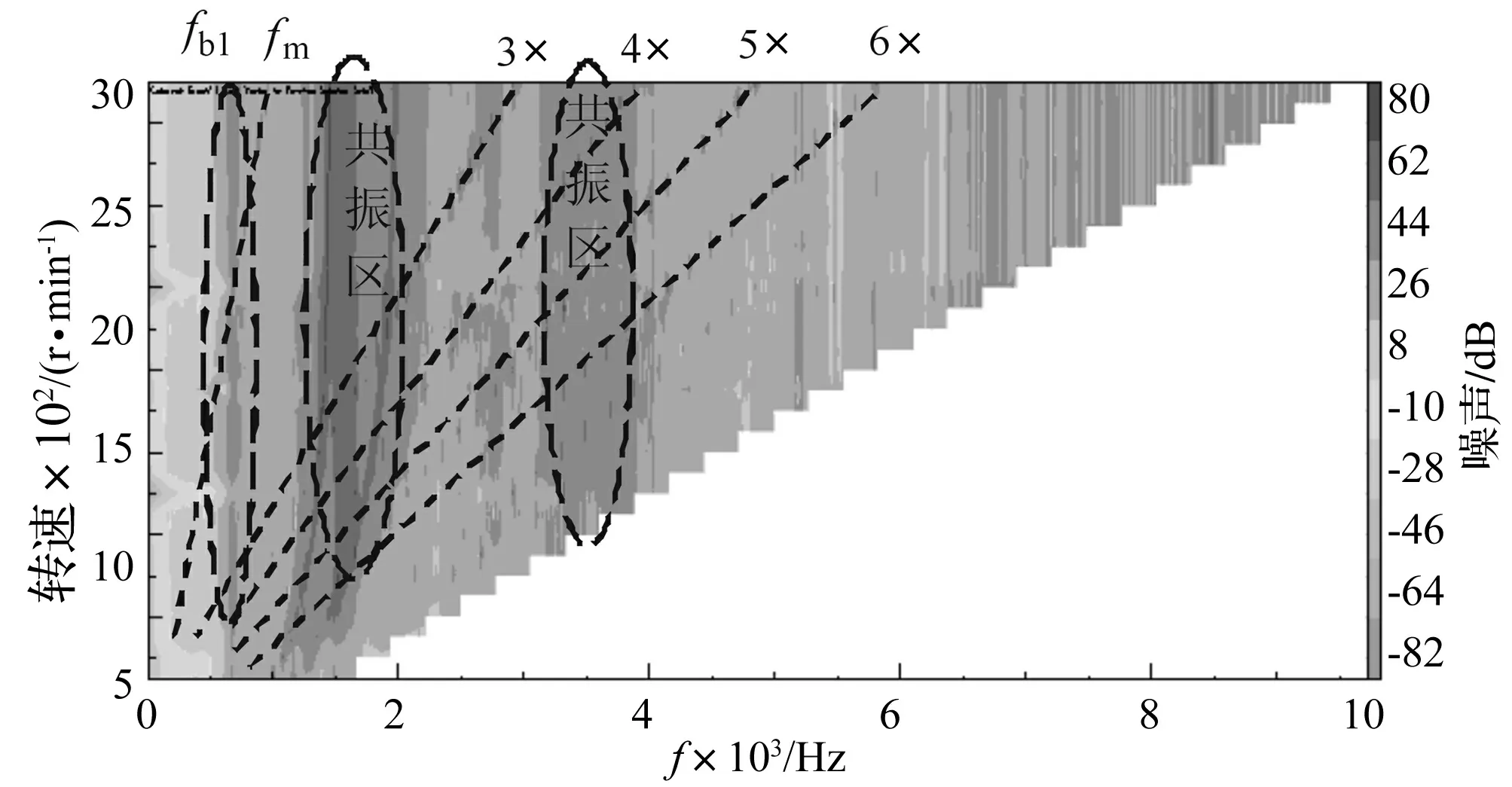
圖6 齒輪箱噪聲輻射瀑布圖

分別計算各轉速下齒輪箱輻射噪聲有效聲壓級，同時將轉速轉換為齒輪線速度，即得到有效聲壓與線速度的關系，如圖7所示，其中曲線a為數值計算結果，b為采用Kato公式計算結果。

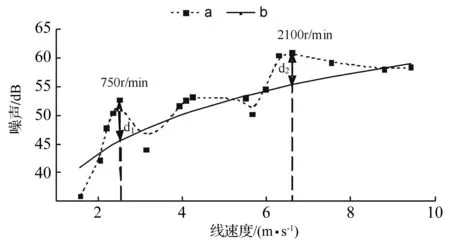
圖7 箱體輻射噪聲隨齒輪線速度的變化

由于Kato公式中并未體現傳動系統及齒輪箱的固有特性，故計算結果隨齒輪線速度的變化趨勢較為平滑，減速器噪聲隨齒輪轉速的增加逐漸增大。采用FEM/BEM計算不僅考慮了傳動系統及減速器的固有特性，還引入齒輪嚙合頻率及其倍頻激勵的作用，故噪聲曲線伴隨有一定的波動。在750 r/min時，由于激勵六次諧波成分與傳動系統第一階固有頻率較為接近，使傳動系統產生了較大的振動，噪聲輻射偏離曲線d1=7 dB；在2 100 r/min時，由于齒輪嚙合力二次諧波成分(1 398 Hz)與齒輪箱第二階固有頻率較為接近，引起了齒輪箱較大的振動，使噪聲輻射偏離曲線d2=5 dB。若去除這兩個共振位置，其他位置兩曲線相差均未超過3 dB，因此仿真計算結果與Kato計算結果基本吻合。

3.2 負載對減速器振動噪聲的影響

對于傳動系統，負載不改變各激勵頻率成分，僅對各頻率成分的幅值有一定影響，并成線性變化。在不改變轉速的前提下，計算了負載分別為0.5×T，T，及3×T(其中T為工作載荷)減速器噪聲輻射，如圖8所示，可以看到隨著負載的增加，減速器輻射噪聲在各個頻率均有所增加，并在激勵基頻及其主要倍頻位置附近增加較為明顯，各峰值位置均未發生改變。

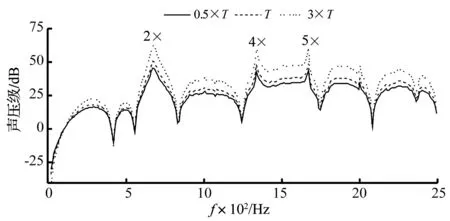
圖8 箱體噪聲隨負載的變化

由式(8)計算了各位置場點等效聲壓級分別為43.66 dB，49.53 dB及55.84 dB，可以發現，在轉速不變時，輻射噪聲與負載的變化符合，Kato公式的函數關系，即:

L(n×T)=20logn+L(T)

(9)

其中：n為負載的比例系數，T為負載，L(T)為負載為T時齒輪箱輻射噪聲。

4 振動噪聲預測公式擬合

4.1 誤差合成方法

在齒輪動力學計算中，通常將誤差合成值當量至嚙合線上進行計算，而齒形誤差和基節偏差均為齒面交線間法向距離的理論值與實際值差的最值，故可直接將兩項誤差進行合成。

如果已知齒輪的齒形誤差ff和基節偏差Fpb值，則可以用代數和來計算齒輪的固有位置誤差，通常情況下齒輪誤差的合成需轉換到節圓上進行度量，此時齒輪固有位置誤差為：

(10)

對于一批合格齒輪來說，齒形總誤差、基節偏差均在其公差范圍內變化，故采用統計方法來計算齒輪短周期誤差[12]，建立精度等級與誤差值的數值關系，如圖10所示，將各精度合成誤差帶入動力學模型中進行計算，計算中取系統轉速為1 000 r/min，為避免計算中出現脫嚙和齒背沖擊等非線性響應，故增大功率至30 kW。

4.2 減速器噪聲預估公式擬合

齒輪精度分別為5、6、7級時的噪聲譜，如圖9所示，與不考慮誤差時相比較，考慮誤差后其噪聲譜在齒輪嚙合頻率位置出現了明顯的峰值，同時在前幾階倍頻位置(4倍頻)的噪聲也明顯增大，對高頻位置其影響不明顯。隨著誤差的增大，各峰值也逐漸增大。

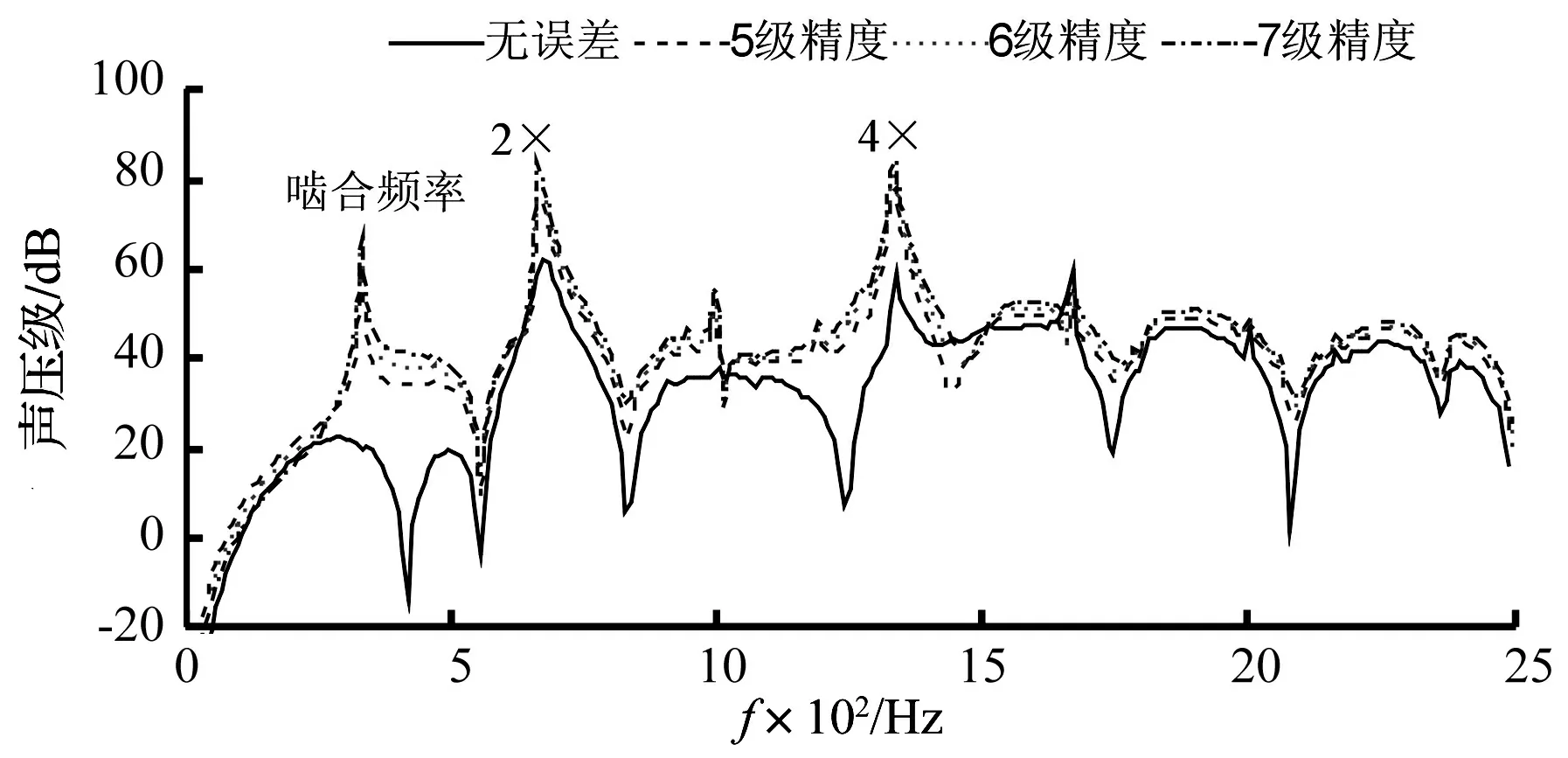
圖9 不同齒輪精度下的噪聲譜

分別計算各精度等級的齒輪箱有效噪聲，得到齒輪箱噪聲輻射隨精度等級變化曲線，如圖10所示。

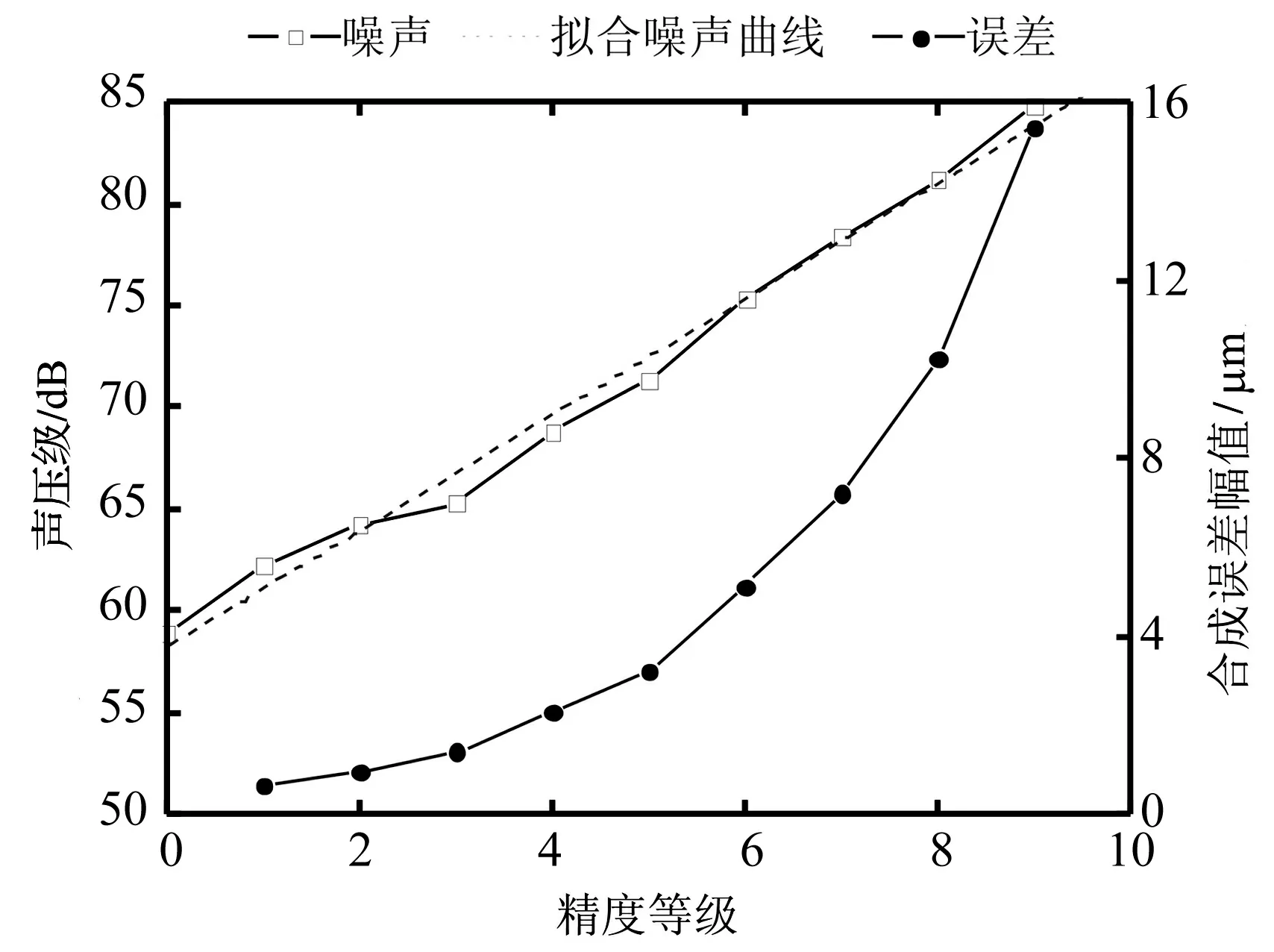
圖10 減速器噪聲及合成誤差隨精度等級的變化

可以看到隨精度等級增加，誤差的增大，齒輪箱有效噪聲呈線性增大，通過擬合可以得到其函數關系為：

Y=A+B·X

(11)

其中：A為無誤差時齒輪箱有效噪聲58.84 dB，B為有效噪聲隨精度等級變化的梯度2.85。

結合Kato公式，得到考慮精度等級的齒輪傳動裝置振動噪聲預估公式如式12所示。

(12)

其中：Q為齒輪精度等級。

4.3 減速器噪聲預估公式擬合

傳動系統轉速及負載不僅影響著誤差激勵在系統動載荷中的頻率成分，還影響各頻率成分的數值，為進一步分析工況條件對誤差激勵的影響，定義齒輪精度每變化一級，減速器噪聲輻射的變化量為減速器噪聲隨齒輪精度的變化率，用符號DQ表示，即

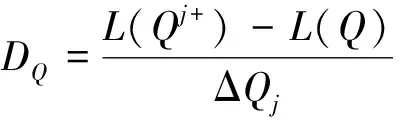
(13)

其中：L(Q)為精度等級為Q時的有效聲壓級；mQ為最高精度等級。

分別計算了轉速為500～3 000 r/min時，減速器輻射噪聲隨誤差的變化率，如圖11(a)所示。可以看到其分布均在2.85附近(最大偏差僅為0.15)，并且未呈現出規律性。可以認為轉速對誤差激勵在該工況范圍內影響不大，在噪聲預估公式擬合中可以不必考慮轉速對誤差項的影響。

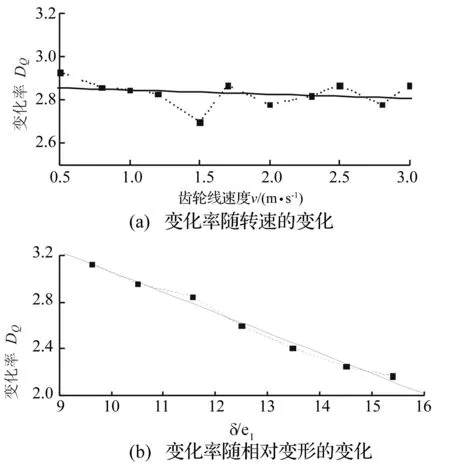
圖11 變化率隨工況條件的變化

分別計算了負載扭矩為230～380 N·m時齒輪箱輻射噪聲，計算中發現當負載增加時齒輪箱輻射噪聲隨精度的變化率逐步減小，而負載本身對誤差激勵并不會產生影響，但是負載的增加會使齒輪彈性變形增加，從而使齒輪剛度激勵影響增加，誤差激勵的影響隨之減弱，最終使噪聲隨誤差的變化率逐漸減小。

在描述噪聲輻射隨精度等級的變化率時，引入相對變形量δr(齒輪副靜變形量與精度等級為1時的合成誤差值的比值)，即：

δr=δ0/e1

(14)

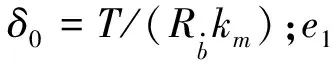
變化率隨相對變形量的變化如圖11(b)所示，可以看到，隨著靜變形量的增加，變化率線性減小，通過擬合可以得到變化率隨相對變形量的函數關系為：

Y=A+B·X

(15)

其中：A為4.78，B為-0.17。

綜合考慮負載及轉速對變化率的影響，得到減速器噪聲預估計算公式為：

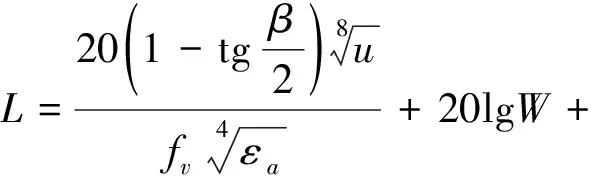
(16)

5 試驗驗證

減速器噪聲測試試驗設施由變頻驅動電機、輸入輸出傳感器、被測傳動裝置、加載裝置、聲學分析儀等組成，布局如圖12所示。測試聲壓時測點距離齒輪箱1 m左右。

圖12 試驗設施布局

試驗中測試兩種工況條件下的減速器輻射噪聲，工況如表3所示。

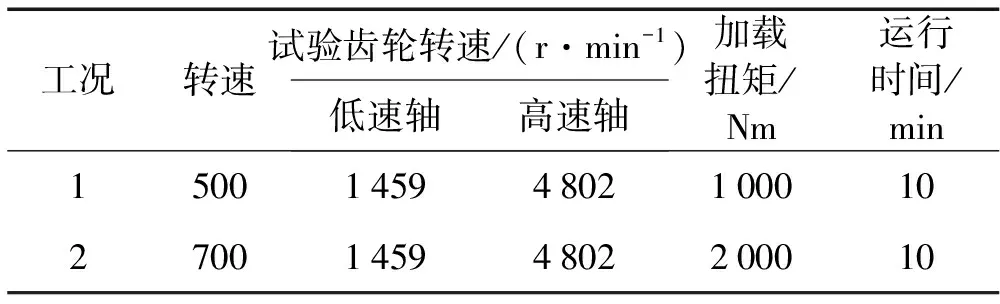
表3 試驗工況條件

試驗中，測試樣機參數如表4所示。

表4 測試樣機參數

分別測得兩種工況下的噪聲頻譜，如圖13所示，工況1條件下嚙合頻率噪聲聲壓幅值為0.12 Pa，工況2條件下嚙合頻率噪聲幅值為0.32 Pa。

(a) 1 000 N·m，500 r/min工況下測量結果

(b) 2 000 N·m，700 r/min工況下測量結果

通過減速器噪聲預估公式16計算的結果與試驗測試結果，如表5所示，可以看到在兩種工況下，預估計算結果與試驗結果均比較吻合。以此證明了預估公式計算的準確性。

表5 預估與測試結果 (dB)

6 結 論

(1) 仿真計算中可考慮傳動系統和減速器的固有特性。若去除共振位置，則通過仿真得到了噪聲隨轉速的變化，與Kato公式所述趨勢基本吻合。

(2) 在轉速不變的條件下，通過仿真計算發現減速器輻射噪聲與負載成20 log函數關系變化，與Kato公式所描述規律一致。

(3) 齒輪箱輻射噪聲隨精度等級基本呈線性變化，綜合考慮誤差與轉速和負載的耦合作用關系，擬合了減速器噪聲預估公式，可實現由減速器基本系統直接預測其輻射噪聲的功能。

(4) 開展了減速器振動噪聲測試試驗，對試驗結果與擬合公式計算結果進行了對照，驗證了減速器噪聲預估公式的準確性。

參 考 文 獻

[1]Yuruzume I, Mizutanz H, Tsubuku T. Transmission errors and noise of spur gears laving uneven tooth profile errors[J]. Journal of Mechanical Design, 1979, 101(4): 268-373.

[2]李潤方,王建軍. 齒輪系統動力學—振動、沖擊、噪聲[M].北京: 科學出版社, 1997.

[3]Teruo M, Toru A, Kanji H. Prediction method of gear noise considering the influence of the tooth flank finishing method[J]. Journal of Vibration,Acoustics, Stress,and Reliability in Design, 1986,108:95-99.

[4]張策,梁鐘. 對于漸開線齒輪噪聲計算公式的修正[J]. 天津大學學報, 1983, 3: 85-91.

ZHANG Ce, LIANG Zhong. A modificatin of the noise calculating formula of the involute gear[J]. Journal of Tianjin University. 1983, 3: 85-91.

[5]朱才朝,秦大同,李潤方. 車身結構振動與車內噪聲聲場耦合分析與控制[J].機械工程學報, 2002, 38(8):54-58.

ZHU Cai-chao, QIN Da-tong, LI Run-fang. Study on coupling between body structure dynamic and interior noise[J]. Chinese Journal of Mechanical Engineering,2002, 38(8)：54-58.

[6]程昊,高煜,張永斌,等. 振動體聲學靈敏度分析的邊界元法[J]. 機械工程學報, 2008, 44(7): 45-51.

CHENG Hao, GAO Yu, ZHANG Yong-bin, et al. Boundary element method for acoustic sensitivity analysis of vibrating structures[J]. Chinese Journal of Mechanical Engineering,2008, 44(7)：45-51.

[7]Bouillard P, Suleau S. Element-free garlekin solutions for helmholtz problems: formulation and numerical assessment of the pollution effect[J]. Computer Methods in Applied Mechanicals and Engineering, 1998, 162: 317-335.

[8]Kato M, Inoue K, Shibata K, et al. Evaluation of sound power radiated by a gearbox[C]. Proc. Inter Gearing’94, 1994. 69-74.

[9]陸波,朱才朝,宋朝省,等.大功率船用齒輪箱耦合非線性動態特性分析及噪聲預估[J].振動與沖擊,2009,28(4):76-80.

LU Bo, ZHU Cai-chao, SONG Chao-sheng, et al. Coupled nonlinear dynamic characteristics analysis and noise predestination of a large burden marine gearbox[J]. Journal of Vibration and Shock, 2009, 28(4): 76-80.

[10]王文平,項昌樂,劉輝. 基于FEM/BEM變速器箱體輻射噪聲的研究. 噪聲與振動控制, 2007,27(5):107-111.

WANG Wenping, XIANG Changle, LIU Hui. Study on the radiation noise of gearbox housing based on FEM/BEM[J]. Noise and Vibration Control, 2007, 27(5): 107-111.

[11]周建星,劉更,馬尚君. 內激勵作用下齒輪箱動態響應與振動噪聲分析[J].振動與沖擊,2011,30(6):234-238.

ZHOU Jian-xing, LIU Geng, MA Shang-jun. Vibration and noise analysis of gear transmission system[J]. Journal of Vibration and Shock,2011, 30(6): 234-238.

[12]卜忠紅. 人字齒行星齒輪傳動系統的動態特性研究[D]. 西安：西北工業大學，2011.